掃雷與演算法:如何隨機化的佈雷(一)
阿新 • • 發佈:2019-06-03
這是通過「掃雷與演算法」小程式來講解演算法的第一章:如何隨機化的進行佈雷,主要介紹了三種不那麼好的方法,希望通過這些不好的方法能讓大家明白第二章要講解的「洗牌演算法」有多牛逼。
補充:「掃雷與演算法」小程式會在寫完後進行開源,釋出在我的 GitHub 上面。
方法一
最想當然的方法就是隨機的在二維區間尋找一個點佈雷即可,程式碼如下:
for (var i = 0; i < mineNumber; i++) {
var row = this.rangeRandom(0, this.rowCount - 1);
//使用數字 9 表示該區域有雷
tmpMineMap[row][col] = 9;
}
這種實現邏輯的一個弊端就是會在已經佈雷的位置再度佈雷,進而導致整個區域的佈雷數量與要求不符合。
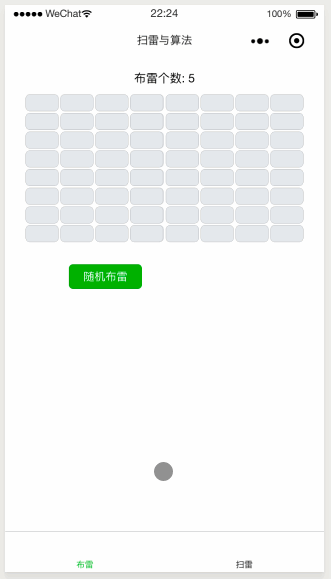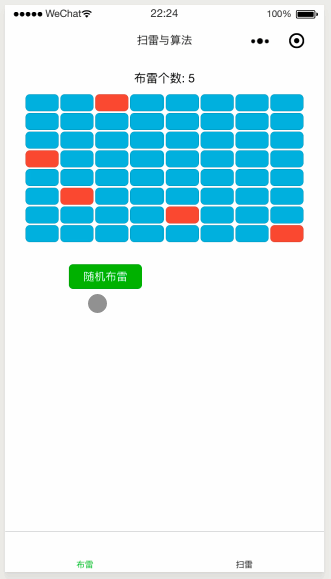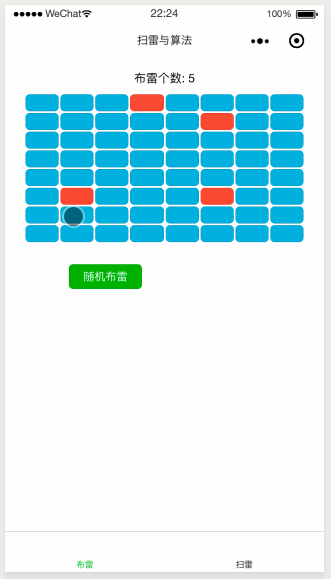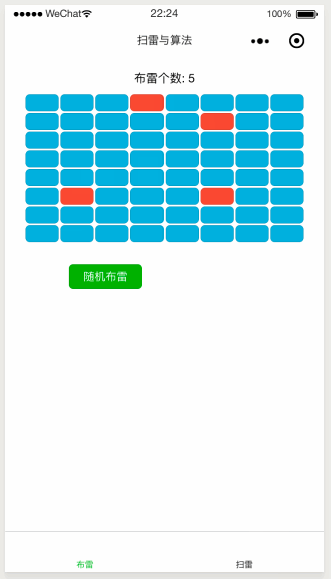
如上圖所示,需要佈雷的個數為 5 ,但在最後一次的隨機佈雷過程中只埋了 4 顆雷。
方法二
方法二是對方法一的改善:既然會重複埋雷,那麼只需要再埋雷的過程中判斷一下該位置是否已經埋雷即可。
- 如果該位置是空的,那麼則佈雷,然後進行尋找新的位置佈下下一顆雷
- 如果該位置已經被安置了雷,那麼就需要重新生成一個位置來安置
程式碼如下:
for (var i = 0; i < mineNumber; i++) {
//通過死迴圈來實現不停的尋找,直到安置好雷
var row = this.rangeRandom(0, this.rowCount - 1);
var col = this.rangeRandom(0, this.colCount - 1);
//用數字 9 表示該區域有雷,如果該位置沒有佈雷,那麼則放置
if (tmpMineMap[row][col] != 9) {
tmpMineMap[row][col] = 9;
//跳出迴圈
break;
}
}
}
使用效果如下:
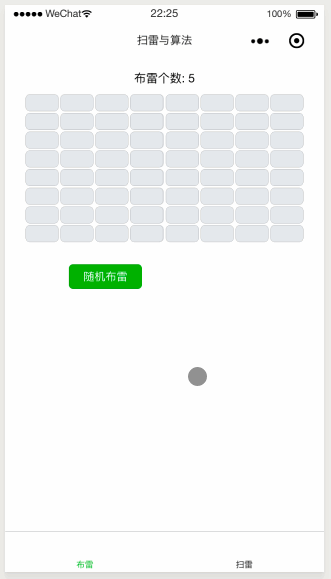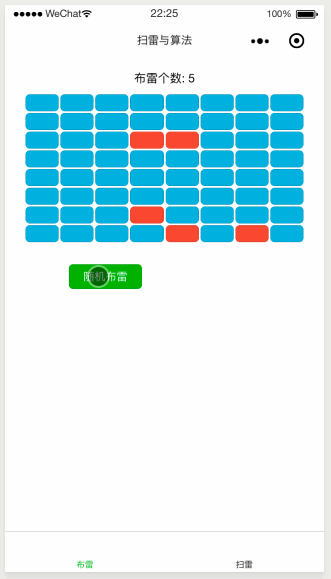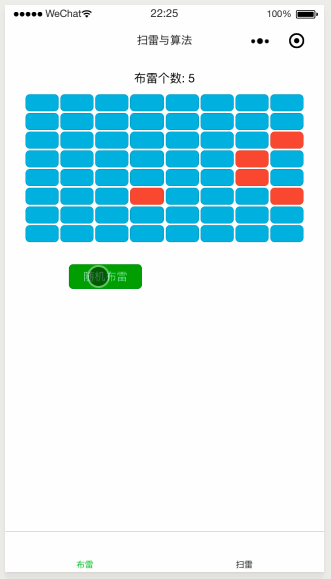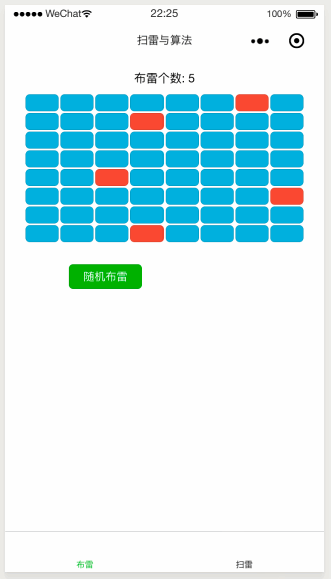
效果貌似挺好的,但小夥伴們可能已經注意到了,上面的程式碼中有一段 死迴圈 程式碼,這就意味著如果棋盤很大,雷區很多,並且你的運氣還不夠好的話,那麼就有可能一直在執行這段 死迴圈 程式碼,進而導致程式的卡死崩潰。
 雖然沒有卡死,但執行時間很久
雖然沒有卡死,但執行時間很久
方法三
第三種方法是先將雷佈置在最前面,然後再不停的打亂。
實現程式碼如下:
//先按順序排列
for (var i = 0; i < mineNumber; i++) {
var row = parseInt(i / this.colCount);
var col = i % this.colCount;
//使用數字 9 表示該區域有雷
tmpMineMap[row][col] = 9;
}
//定義交換的次數,次數越多越混亂隨機
var swapTime = 100;
for (var i = 0; i < swapTime; i++) {
//隨機位置1
var row1 = this.rangeRandom(0, this.rowCount - 1);
var col1 = this.rangeRandom(0, this.colCount - 1);
//隨機位置2
var row2 = this.rangeRandom(0, this.rowCount - 1);
var col2 = this.rangeRandom(0, this.colCount - 1);
//交換兩個位置
var temp = tmpMineMap[row1][col1];
tmpMineMap[row1][col1] = tmpMineMap[row2][col2];
tmpMineMap[row2][col2] = temp;
}

這種方法的一個弊端就是對於 swapTime 的依賴程度很高,如果設定的互動次數少了,大部分雷都還是按照一開始的順序安置,都在最前面的位置,全部的雷並不是隨機排放。
最重要的一點是:每個位置安置雷的概率並不是等可能的,也就意味著它不能做到隨機化。
我嘗試過在小程式上進行概率模擬,但每次都會卡死了,後續發現能優化繼續模擬出概率來的話再補上。
總結
在大部分情況下,方法二 與 方法三 是可以滿足我們隨機化處理的過程的,但方法二有可能執行卡死崩潰,方法三中每個位置安置雷的概率並不是等可能的。
❤️ 看完三件事:
如果你覺得這篇內容對你挺有啟發,我想邀請你幫我三個忙:
- 點贊,讓更多的人也能看到這篇內容(收藏不點贊,都是耍流氓 -_-)
- 關注我和專欄,讓我們成為長期關係
- 關注公眾號「五分鐘學演算法」,第一時間閱讀最新的演算法文章,公眾號後臺回覆 1024 送你 50 本 演算法程式設計書籍。
