一、簡介

紅黑樹（Red Black Tree）是一棵二叉查詢樹，在每個節點增加一個屬性表示節點顏色，值為紅色（Red）或者黑色（Black）。紅黑樹也是“平衡”樹中的一種，通過對任何一條從根到葉子的路徑上各個節點的顏色來進行約束，確保沒有一條路徑會比其他路徑長出2倍，因而是“近似平衡”的。對平衡性的要求相較於AVL樹更寬鬆。

二、紅黑樹性質

一棵紅黑樹是滿足下面5條紅黑性質的二叉查詢樹：

1. 每個節點要麼是紅色，要麼是黑色；
2. 根節點是黑色；
3. 每個葉節點（NIL或者空節點）是黑色；
4. 如果一個節點是紅色，則它的兩個子節點都是黑色；
5. 對於每個節點，從該節點到其所有後代葉節點的路徑上，均包含相同數目的黑色節點。

下圖就是一棵紅黑樹：

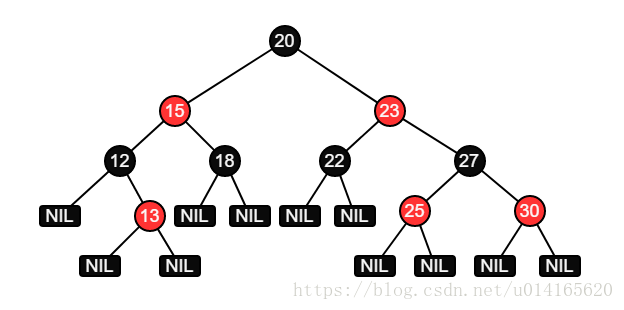
插入一個新節點或者刪除一個節點時，可能會導致違反上述紅黑樹性質，所以需要通過改變節點顏色和旋轉來維護這些性質。
旋轉直觀效果如下：
左旋：

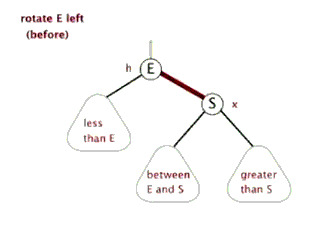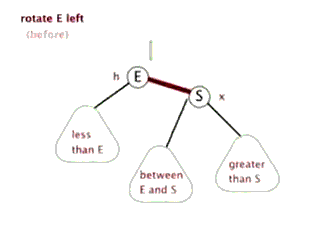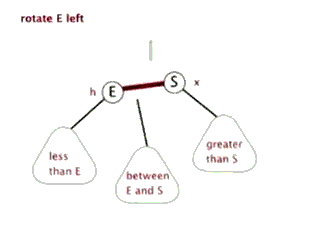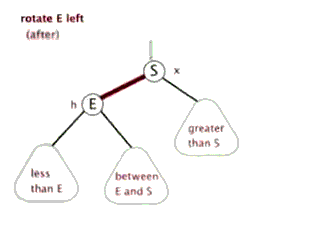
右旋：

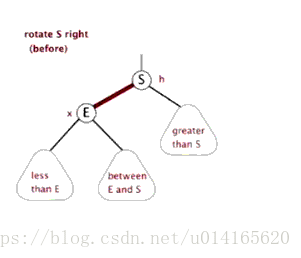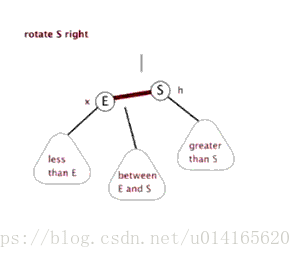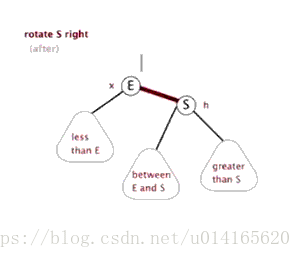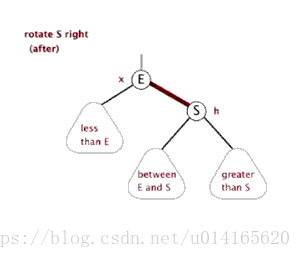
關於旋轉的詳細介紹，可以參考AVL樹的旋轉圖解，紅黑樹的旋轉與AVL樹的旋轉類似。

三、插入

因為紅黑樹也是一棵二叉查詢樹，所以定位新節點的插入位置與二叉查詢樹插入操作一樣，這裡主要介紹插入新節點後維護紅黑樹性質涉及的調整操作，即改變節點顏色和旋轉。
插入新節點時，假設X為新插入節點，維護紅黑樹性質過程中涉及如下幾個節：

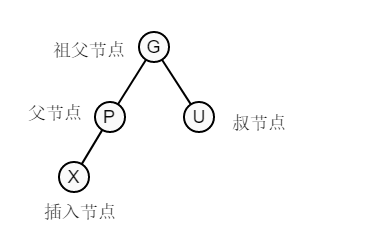
為了不違反性質5（對於每個節點，從該節點到其所有後代葉節點的路徑上，均包含相同數目的黑色節點），新插入的節點都為紅色。

插入新節點X後包含以下幾種情況：
情況1：原紅黑樹為空，插入後X為根節點，則根據性質2，直接將節點X塗黑即可；
情況2：X的父節點P為黑色，插入X不會違反紅黑樹性質，直接插入即可，不需調整；
情況3：X的父節點P為紅色
此時違反性質4（如果一個節點是紅色，則它的兩個子節點都是黑色），需要調整。此時，包含6種情況，按父節點P是祖父節點G的左孩子left或者右孩子right劃分，處理方式是對稱的，這裡以P是G的左孩子left為例進行介紹。其中，包含3種情況：
情況3-1：叔節點U為紅色
將P塗為黑色以保持性質4，此時違反性質5，再將G塗為紅色，同時U塗為黑色以保持性質5。然後X=G，G作為新節點X，繼續維護。

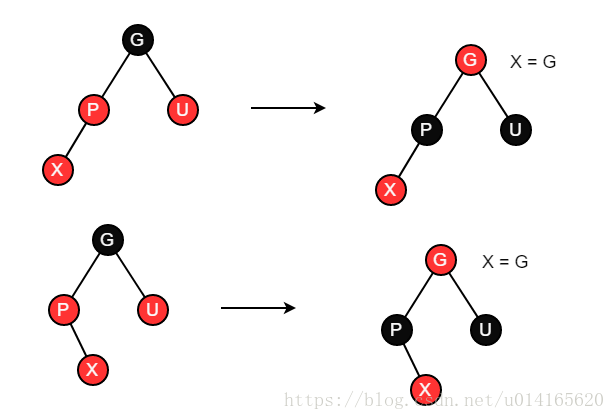
情況3-2：叔節點U為黑色，新節點X為其父節點P的右節點right；
情況3-3：叔節點U為黑色，新節點X為其父節點P的右節點left。

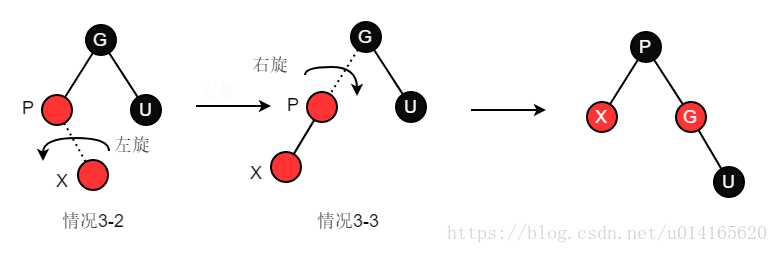
情況3-2通過一個左旋，變成情況3-3。對於情況3-3，X、P都是紅色，違反了性質4，所以將P塗為黑色，此時左邊這條路徑多了一個黑色節點，違反了性質5，所以將G塗為紅色（因為P是紅色，所以原來G一定是黑色），這樣右邊那條路徑比以前少了一個黑色節點，同樣違反性質5，所以通過右旋，將黑色P向上提。調整結束，無需繼續上慮。
情況3對應調整虛擬碼如下：

while P.color == RED
    if P == G.left
        if U == RED                            //情況3-1
            P.color = BLACK
            U.color = BLACK
            G.color = RED
            X = G
        else if X == P.right                   //情況3-2
            X = X.p // X與P互換位置
            left_rotation()  //左旋
        P.color = BLACK                        //情況3-3
        G.color = Red
        right_rotation()   //右旋
    else
        //與上面3種情況對稱
root.color = BLACK

四、刪除

紅黑樹的刪除操作，是在二叉查詢樹刪除操作基礎上增加部分內容，主要是增加維護紅黑樹性質的調整操作，與插入操作一樣，調整方式包括：改變節點顏色、旋轉。下面主要對調整操作進行介紹。
假設刪除節點為X，維護紅黑樹性質的調整過程涉及如下幾個節點：

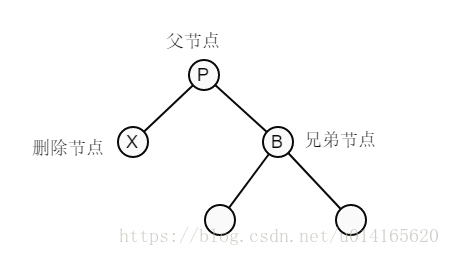
紅黑樹刪除調整包含8種情況，按照刪除節點為其父節點的左孩子left或者右孩子right劃分，處理方式是對稱的。這裡以刪除節點X為其父節點P的左孩子left為例進行介紹。其中。包含4種
紅黑樹刪除操作包含以下幾種情況：
情況1：刪除節點X為紅色，不會導致違反5條紅黑樹性質，無需調整；
情況2：當刪除節點為根節點時，直接刪除，無需調整；
當刪除節點為黑色，且不為根節點時，刪除調整包含8種情況，按照刪除節點為其父節點的左孩子left或者右孩子right劃分，處理方式是對稱的。這裡以刪除節點X為其父節點P的左孩子left為例進行介紹。其中，包含4種情況（3~6），如下圖所以，圖中無色節點（如情況4中的節點2），既可以是紅色節點，也可以是黑色節點：

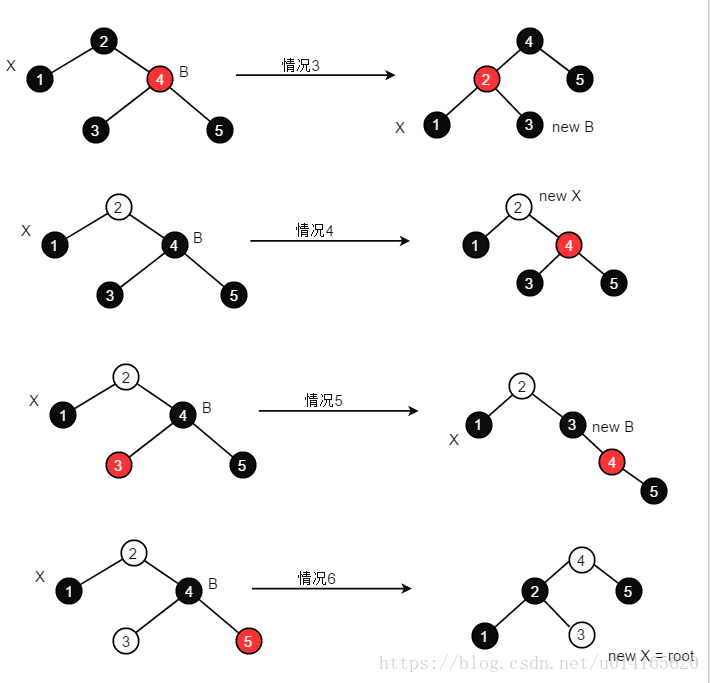
情況3：兄弟節點B是紅色；
情況4：兄弟節點B是黑色，且B的兩個子節點都是黑色；
情況5：兄弟節點B是黑色，且B的左孩子是紅色，右孩子是黑色；
情況6：兄弟節點B是黑色，且B的右孩子是紅色。

虛擬碼如下：

while X != root and X.color == BlACK
    if X == X.p.left
        B = X.p.right
        if B.color == RED
            B.color = BLACK
            X.p.color = RED
            left_rotation(X.p)
            B = X.p.right
        if B.left.color == BLACK and B.right.color == BLACK
            B.color = RED
            x = X.p
        else if B.right.color == BLACK
            B.left.color = BLACK
            B.color = RED
            right_rotation(B)
            B = X.p.right
        B.color = X.p.color
        X.p.color = BLACK
        B.right.color = BLACK
        left_rotation(X.p)
        X = root
    else
        X 為其父節點右孩子，處理方式對稱
X.color = BLACK

五、紅黑樹與AVL樹比較

紅黑樹與AVL樹都是“平衡”二叉查詢樹中的一種，AVL樹對平衡性的要求更高，AVL樹要求每個節點左右子樹高度差不超過1，而紅黑樹節點的左右子樹高度差可能會大於1，是一種“近似平衡”。紅黑樹通過節點顏色控制，用非嚴格的平衡來換取增刪節點時旋轉次數的降低，任何不平衡都會在三次旋轉之內解決，而AVL是嚴格平衡樹，因此在增加或者刪除節點的時候，根據不同情況，旋轉的次數比紅黑樹要多。因此，AVL樹查詢效率比紅黑樹高。但因為平衡性要求更高，每次插入刪除會進行更多的平衡調整，所以AVL樹插入刪除效率相對較慢。

個人總結，如有錯誤，感謝指正！

參考《演算法導論》