圖形變換中涉及到的數學知識(向量叉乘、矩陣相乘、齊次座標)
阿新 • • 發佈:2018-11-16
文章目錄
1. 向量
1.1 點乘
兩個n維向量點乘:
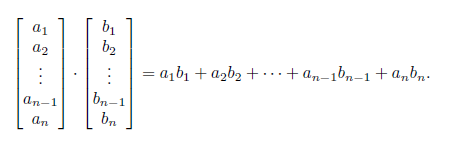
二維向量的點乘:向量的模長相乘再乘以夾角餘弦值。
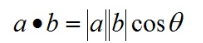
- 點乘的結果是一個數值(標量)。
- 幾何意義:b向量再a向量上的投影長度。
1.2 叉乘
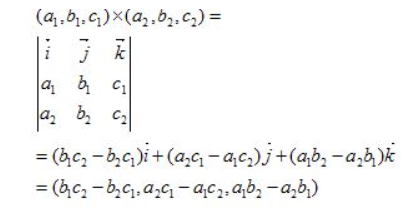
- 結果:是一個向量(向量)。
- 幾何意義:向量a和向量b叉乘的
2. 矩陣
2.1 矩陣乘法

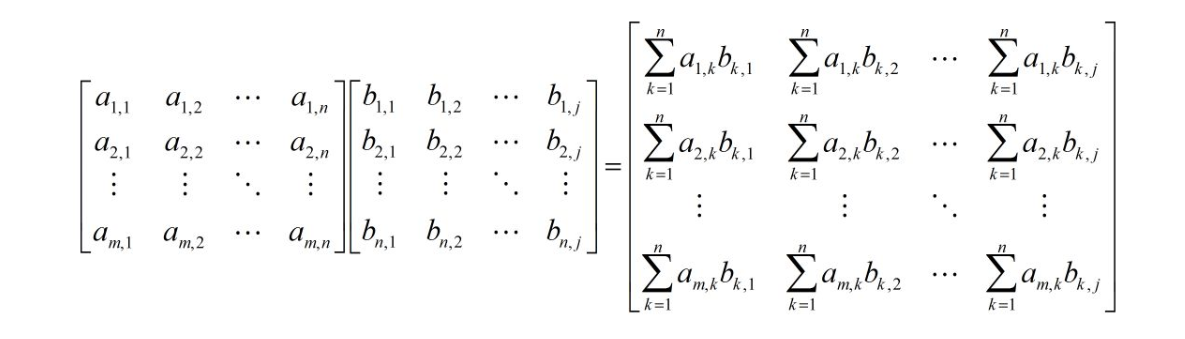
舉例:

3. 齊次座標
-
齊次座標就是圖形變換過程中為了方便計算產生的概念。齊次座標是將一個原本是n維的向量用一個n+1維向量來表示。
-
例如:二維點(x,y)的齊次座標表示為(hx,hy,h)。由此可以看出,一個點的齊次表示是不唯一的,齊次座標的h取不同的值都表示的是同一個點,比如齊次座標(8,4,2)、(4,2,1)表示的都是二維點(4,2)。
-
向量的w分量也叫齊次座標。想要從齊次向量得到3D向量,我們可以把x、y和z座標分別除以w座標。我們通常不會注意這個問題,因為w分量通常是1.0。
-
如果一個向量的齊次座標是0,這個座標就是方向向量(Direction Vector),因為w座標是0,這個向量就不能位移(譯註:這也就是我們說的不能位移一個方向)。 它可以理解為一個無窮遠的點。n+1維的齊次座標中如果h=0,實際上就表示了n維空間的一個無窮遠點。
-
使用齊次座標有幾點好處:它允許我們在3D向量上進行位移(如果沒有w分量我們是不能位移向量的)
