原文地址：OpenGL

變換

原文	Transformations
作者	JoeyDeVries
翻譯	Django, Krasjet, BLumia
校對	暫未校對

儘管我們現在已經知道了如何建立一個物體、著色、加入紋理，給它們一些細節的表現，但因為它們都還是靜態的物體，仍是不夠有趣。我們可以嘗試著在每一幀改變物體的頂點並且重配置緩衝區從而使它們移動，但這太繁瑣了，而且會消耗很多的處理時間。我們現在有一個更好的解決方案，使用（多個）矩陣(Matrix)物件可以更好的變換(Transform)一個物體。當然，這並不是說我們會去討論武術和數字虛擬世界（譯註：Matrix同樣也是電影「黑客帝國」的英文名，電影中人類生活在數字虛擬世界，主角會武術）。

矩陣是一種非常有用的數學工具，儘管聽起來可能有些嚇人，不過一旦你理解了它們後，它們會變得非常有用。在討論矩陣的過程中，我們需要使用到一些數學知識。對於一些願意多瞭解這些知識的讀者，我會附加一些資源給你們閱讀。

為了深入瞭解變換，我們首先要在討論矩陣之前進一步瞭解一下向量。這一節的目標是讓你擁有將來需要的最基礎的數學背景知識。如果你發現這節十分困難，儘量嘗試去理解它們，當你以後需要它們的時候回過頭來複習這些概念。

向量

向量最基本的定義就是一個方向。或者更正式的說，向量有一個方向(Direction)和大小(Magnitude，也叫做強度或長度)。你可以把向量想像成一個藏寶圖上的指示：“向左走10步，向北走3步，然後向右走5步”；“左”就是方向，“10步”就是向量的長度。那麼這個藏寶圖的指示一共有3個向量。向量可以在任意維度(Dimension)上，但是我們通常只使用2至4維。如果一個向量有2個維度，它表示一個平面的方向(想象一下2D的影象)，當它有3個維度的時候它可以表達一個3D世界的方向。

下面你會看到3個向量，每個向量在2D影象中都用一個箭頭(x, y)表示。我們在2D圖片中展示這些向量，因為這樣子會更直觀一點。你可以把這些2D向量當做z座標為0的3D向量。由於向量表示的是方向，起始於何處並不會改變它的值。下圖我們可以看到向量v¯v¯和w¯w¯是相等的，儘管他們的起始點不同：

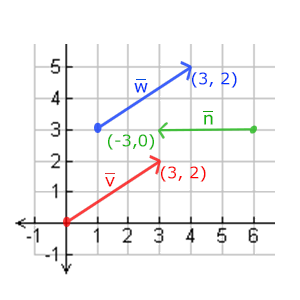
數學家喜歡在字母上面加一橫表示向量，比如說v¯v¯。當用在公式中時它們通常是這樣的：

 

v¯=⎛⎝⎜xyz⎞⎠⎟v¯=(xyz)

由於向量是一個方向，所以有些時候會很難形象地將它們用位置(Position)表示出來。為了讓其更為直觀，我們通常設定這個方向的原點為(0, 0, 0)，然後指向一個方向，對應一個點，使其變為位置向量(Position Vector)（你也可以把起點設定為其他的點，然後說：這個向量從這個點起始指向另一個點）。比如說位置向量(3, 5)在影象中的起點會是(0, 0)，並會指向(3, 5)。我們可以使用向量在2D或3D空間中表示方向與

位置.

和普通數字一樣，我們也可以用向量進行多種運算（其中一些你可能已經看到過了）。

向量與標量運算

標量(Scalar)只是一個數字（或者說是僅有一個分量的向量）。當把一個向量加/減/乘/除一個標量，我們可以簡單的把向量的每個分量分別進行該運算。對於加法來說會像這樣:

 

⎛⎝⎜123⎞⎠⎟+x=⎛⎝⎜1+x2+x3+x⎞⎠⎟(123)+x=(1+x2+x3+x)

其中的+可以是+，-，·或÷，其中·是乘號。注意－和÷運算時不能顛倒（標量-/÷向量），因為顛倒的運算是沒有定義的。

向量取反

對一個向量取反(Negate)會將其方向逆轉。一個指向東北的向量取反後就指向西南方向了。我們在一個向量的每個分量前加負號就可以實現取反了（或者說用-1數乘該向量）:

 

−v¯=−⎛⎝⎜vxvyvz⎞⎠⎟=⎛⎝⎜−vx−vy−vz⎞⎠⎟−v¯=−(vxvyvz)=(−vx−vy−vz)

向量加減

向量的加法可以被定義為是分量的(Component-wise)相加，即將一個向量中的每一個分量加上另一個向量的對應分量：

 

v¯=⎛⎝⎜123⎞⎠⎟,k¯=⎛⎝⎜456⎞⎠⎟→v¯+k¯=⎛⎝⎜1+42+53+6⎞⎠⎟=⎛⎝⎜579⎞⎠⎟v¯=(123),k¯=(456)→v¯+k¯=(1+42+53+6)=(579)

向量v = (4, 2)和k = (1, 2)可以直觀地表示為：

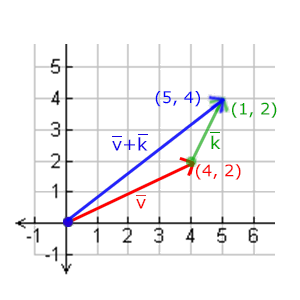
就像普通數字的加減一樣，向量的減法等於加上第二個向量的相反向量：

 

v¯=⎛⎝⎜123⎞⎠⎟,k¯=⎛⎝⎜456⎞⎠⎟→v¯+−k¯=⎛⎝⎜1+(−4)2+(−5)3+(−6)⎞⎠⎟=⎛⎝⎜−3−3−3⎞⎠⎟v¯=(123),k¯=(456)→v¯+−k¯=(1+(−4)2+(−5)3+(−6))=(−3−3−3)

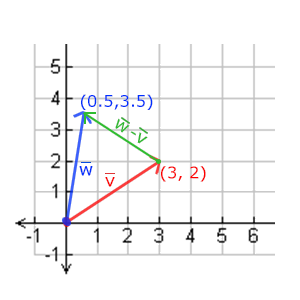
兩個向量的相減會得到這兩個向量指向位置的差。這在我們想要獲取兩點的差會非常有用。

長度

我們使用勾股定理(Pythagoras Theorem)來獲取向量的長度(Length)/大小(Magnitude)。如果你把向量的x與y分量畫出來，該向量會和x與y分量為邊形成一個三角形:

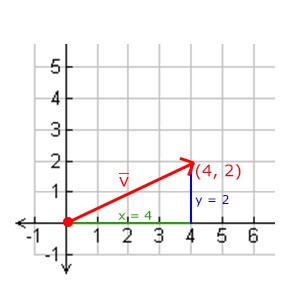
因為兩條邊（x和y）是已知的，如果希望知道斜邊v¯v¯的長度，我們可以直接通過勾股定理來計算：

 

||v¯||=x2+y2−−−−−−√||v¯||=x2+y2

||v¯||||v¯||表示向量v¯v¯的長度，我們也可以加上z2z2把這個公式拓展到三維空間。

例子中向量(4, 2)的長度等於：

 

||v¯||=42+22−−−−−−√=16+4−−−−−√=20−−√=4.47||v¯||=42+22=16+4=20=4.47

結果是4.47。

有一個特殊型別的向量叫做單位向量(Unit Vector)。單位向量有一個特別的性質——它的長度是1。我們可以用任意向量的每個分量除以向量的長度得到它的單位向量n^n^：

 

n^=v¯||v¯||n^=v¯||v¯||

我們把這種方法叫做一個向量的標準化(Normalizing)。單位向量頭上有一個^樣子的記號。通常單位向量會變得很有用，特別是在我們只關心方向不關心長度的時候（如果改變向量的長度，它的方向並不會改變）。

向量相乘

兩個向量相乘是一種很奇怪的情況。普通的乘法在向量上是沒有定義的，因為它在視覺上是沒有意義的。但是在相乘的時候我們有兩種特定情況可以選擇：一個是點乘(Dot Product)，記作v¯⋅k¯v¯⋅k¯，另一個是叉乘(Cross Product)，記作v¯×k¯v¯×k¯。

點乘

兩個向量的點乘等於它們的數乘結果乘以兩個向量之間夾角的餘弦值。可能聽起來有點費解，我們來看一下公式：

 

v¯⋅k¯=||v¯||⋅||k¯||⋅cosθv¯⋅k¯=||v¯||⋅||k¯||⋅cos⁡θ

它們之間的夾角記作θθ。為什麼這很有用？想象如果v¯v¯和k¯k¯都是單位向量，它們的長度會等於1。這樣公式會有效簡化成：

 

v¯⋅k¯=1⋅1⋅cosθ=cosθv¯⋅k¯=1⋅1⋅cos⁡θ=cos⁡θ

現在點積只定義了兩個向量的夾角。你也許記得90度的餘弦值是0，0度的餘弦值是1。使用點乘可以很容易測試兩個向量是否正交(Orthogonal)或平行（正交意味著兩個向量互為直角）。如果你想要了解更多關於正弦或餘弦函式的知識，我推薦你看可汗學院的基礎三角學視訊。

你也可以通過點乘的結果計算兩個非單位向量的夾角，點乘的結果除以兩個向量的長度之積，得到的結果就是夾角的餘弦值，即cosθcosθ。

譯註：通過上面點乘定義式可推出：

 

cosθ=v¯⋅k¯||v¯||⋅||k¯||cos⁡θ=v¯⋅k¯||v¯||⋅||k¯||

所以，我們該如何計算點乘呢？點乘是通過將對應分量逐個相乘，然後再把所得積相加來計算的。兩個單位向量的（你可以驗證它們的長度都為1）點乘會像是這樣：

 

⎛⎝⎜0.6−0.80⎞⎠⎟⋅⎛⎝⎜010⎞⎠⎟=(0.6∗0)+(−0.8∗1)+(0∗0)=−0.8(0.6−0.80)⋅(010)=(0.6∗0)+(−0.8∗1)+(0∗0)=−0.8

要計算兩個單位向量間的夾角，我們可以使用反餘弦函式cos−1cos−1 ，可得結果是143.1度。現在我們很快就計算出了這兩個向量的夾角。點乘會在計算光照的時候非常有用。

叉乘

叉乘只在3D空間中有定義，它需要兩個不平行向量作為輸入，生成一個正交於兩個輸入向量的第三個向量。如果輸入的兩個向量也是正交的，那麼叉乘之後將會產生3個互相正交的向量。接下來的教程中這會非常有用。下面的圖片展示了3D空間中叉乘的樣子：

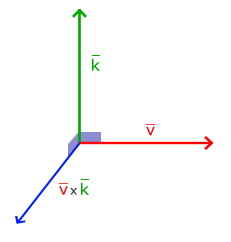
不同於其他運算，如果你沒有鑽研過線性代數，可能會覺得叉乘很反直覺，所以只記住公式就沒問題啦（記不住也沒問題）。下面你會看到兩個正交向量A和B叉積：

 

⎛⎝⎜AxAyAz⎞⎠⎟×⎛⎝⎜BxByBz⎞⎠⎟=⎛⎝⎜Ay⋅Bz−Az⋅ByAz⋅Bx−Ax⋅BzAx⋅By−Ay⋅Bx⎞⎠⎟(AxAyAz)×(BxByBz)=(Ay⋅Bz−Az⋅ByAz⋅Bx−Ax⋅BzAx⋅By−Ay⋅Bx)

是不是看起來毫無頭緒？不過只要你按照步驟來了，你就能得到一個正交於兩個輸入向量的第三個向量。

矩陣

現在我們已經討論了向量的全部內容，是時候看看矩陣了！簡單來說矩陣就是一個矩形的數字、符號或表示式陣列。矩陣中每一項叫做矩陣的元素(Element)。下面是一個2×3矩陣的例子：

 

[142536][123456]

矩陣可以通過(i, j)進行索引，i是行，j是列，這就是上面的矩陣叫做2×3矩陣的原因（3列2行，也叫做矩陣的維度(Dimension)）。這與你在索引2D影象時的(x, y)相反，獲取4的索引是(2, 1)（第二行，第一列）（譯註：如果是影象索引應該是(1, 2)，先算列，再算行）。

矩陣基本也就是這些了，它就是一個矩形的數學表示式陣列。和向量一樣，矩陣也有非常漂亮的數學屬性。矩陣有幾個運算，分別是：矩陣加法、減法和乘法。

矩陣的加減

矩陣與標量之間的加減定義如下：

 

[1324]+3=[1+33+32+34+3]=[4657][1234]+3=[1+32+33+34+3]=[4567]

標量值要加到矩陣的每一個元素上。矩陣與標量的減法也相似：

 

[1324]−3=[1−33−32−34−3]=[−20−11][1234]−3=[1−32−33−34−3]=[−2−101]

矩陣與矩陣之間的加減就是兩個矩陣對應元素的加減運算，所以總體的規則和與標量運算是差不多的，只不過在相同索引下的元素才能進行運算。這也就是說加法和減法只對同維度的矩陣才是有定義的。一個3×2矩陣和一個2×3矩陣（或一個3×3矩陣與4×4矩陣）是不能進行加減的。我們看看兩個2×2矩陣是怎樣相加的：

 

[1324]+[5768]=[1+53+72+64+8]=[610812][1234]+[5678]=[1+52+63+74+8]=[681012]

同樣的法則也適用於減法：

 

[4126]−[2041]=[4−21−02−46−1]=[21−25][4216]−[2401]=[4−22−41−06−1]=[2−215]

矩陣的數乘

和矩陣與標量的加減一樣，矩陣與標量之間的乘法也是矩陣的每一個元素分別乘以該標量。下面的例子展示了乘法的過程：

 

2⋅[1324]=[2⋅12⋅32⋅22⋅4]=[2648]2⋅[1234]=[2⋅12⋅22⋅32⋅4]=[2468]

現在我們也就能明白為什麼這些單獨的數字要叫做標量(Scalar)了。簡單來說，標量就是用它的值縮放(Scale)矩陣的所有元素（譯註：注意Scalar是由Scale + -ar演變過來的）。前面那個例子中，所有的元素都被放大了2倍。

到目前為止都還好，我們的例子都不復雜。不過矩陣與矩陣的乘法就不一樣了。

矩陣相乘

矩陣之間的乘法不見得有多複雜，但的確很難讓人適應。矩陣乘法基本上意味著遵照規定好的法則進行相乘。當然，相乘還有一些限制：

1. 只有當左側矩陣的列數與右側矩陣的行數相等，兩個矩陣才能相乘。
2. 矩陣相乘不遵守交換律(Commutative)，也就是說A⋅B≠B⋅AA⋅B≠B⋅A。

我們先看一個兩個2×2矩陣相乘的例子：

 

[1324]⋅[5768]=[1⋅5+2⋅73⋅5+4⋅71⋅6+2⋅83⋅6+4⋅8]=[19432250][1234]⋅[5678]=[1⋅5+2⋅71⋅6+2⋅83⋅5+4⋅73⋅6+4⋅8]=[19224350]

現在你可能會在想了：天哪，剛剛到底發生了什麼? 矩陣的乘法是一系列乘法和加法組合的結果，它使用到了左側矩陣的行和右側矩陣的列。我們可以看下面的圖片：

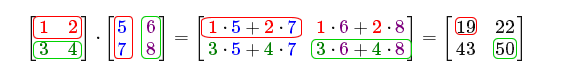
我們首先把左側矩陣的行和右側矩陣的列拿出來。這些挑出來行和列將決定我們該計算結果2x2矩陣的哪個輸出值。如果取的是左矩陣的第一行，輸出值就會出現在結果矩陣的第一行。接下來再取一列，如果我們取的是右矩陣的第一列，最終值則會出現在結果矩陣的第一列。這正是紅框裡的情況。如果想計算結果矩陣右下角的值，我們要用第一個矩陣的第二行和第二個矩陣的第二列（譯註：簡單來說就是結果矩陣的元素的行取決於第一個矩陣，列取決於第二個矩陣）。

計算一項的結果值的方式是先計算左側矩陣對應行和右側矩陣對應列的第一個元素之積，然後是第二個，第三個，第四個等等，然後把所有的乘積相加，這就是結果了。現在我們就能解釋為什麼左側矩陣的列數必須和右側矩陣的行數相等了，如果不相等這一步的運算就無法完成了！

結果矩陣的維度是(n, m)，n等於左側矩陣的行數，m等於右側矩陣的列數。

如果在腦子裡想象出這一乘法有些困難，別擔心。不斷地動手計算，如果遇到困難再回頭看這頁的內容。隨著時間流逝，矩陣乘法對你來說會變成很自然的事。

我們用一個更大的例子來結束對矩陣相乘的討論。試著使用顏色來尋找規律。作為一個有用的練習，你可以試著自己解答一下這個乘法問題，再將你的結果和圖中的這個進行對比（如果用筆計算，你很快就能掌握它們）。

 

⎡⎣⎢400281010⎤⎦⎥⋅⎡⎣⎢429204142⎤⎦⎥=⎡⎣⎢4⋅4+2⋅2+0⋅90⋅4+8⋅2+1⋅90⋅4+1⋅2+0⋅94⋅2+2⋅0+0⋅40⋅2+8⋅0+1⋅40⋅2+1⋅0+0⋅44⋅1+2⋅4+0⋅20⋅1+8⋅4+1⋅20⋅1+1⋅4+0⋅2⎤⎦⎥=⎡⎣⎢2025284012344⎤⎦⎥[420081010]⋅[421204942]=[4⋅4+2⋅2+0⋅94⋅2+2⋅0+0⋅44⋅1+2⋅4+0⋅20⋅4+8⋅2+1⋅90⋅2+8⋅0+1⋅40⋅1+8⋅4+1⋅20⋅4+1⋅2+0⋅90⋅2+1⋅0+0⋅40⋅1+1⋅4+0⋅2]=[2081225434204]

可以看到，矩陣相乘非常繁瑣而容易出錯（這也是我們通常讓計算機做這件事的原因），而且當矩陣變大以後很快就會出現問題。如果你仍然希望瞭解更多，或對矩陣的數學性質感到好奇，我強烈推薦你看看可汗學院的矩陣教程。

不管怎樣，現在我們知道如何進行矩陣相乘了，我們可以開始學習好東西了。

矩陣與向量相乘

目前為止，通過這些教程我們已經相當瞭解向量了。我們用向量來表示位置，表示顏色，甚至是紋理座標。讓我們更深入瞭解一下向量，它其實就是一個N×1矩陣，N表示向量分量的個數（也叫N維(N-dimensional)向量）。如果你仔細思考一下就會明白。向量和矩陣一樣都是一個數字序列，但它只有1列。那麼，這個新的定義對我們有什麼幫助呢？如果我們有一個M×N矩陣，我們可以用這個矩陣乘以我們的N×1向量，因為這個矩陣的列數等於向量的行數，所以它們就能相乘。

但是為什麼我們會關心矩陣能否乘以一個向量？好吧，正巧，很多有趣的2D/3D變換都可以放在一個矩陣中，用這個矩陣乘以我們的向量將變換(Transform)這個向量。如果你仍然有些困惑，我們來看一些例子，你很快就能明白了。

單位矩陣

在OpenGL中，由於某些原因我們通常使用4×4的變換矩陣，而其中最重要的原因就是大部分的向量都是4分量的。我們能想到的最簡單的變換矩陣就是單位矩陣(Identity Matrix)。單位矩陣是一個除了對角線以外都是0的N×N矩陣。在下式中可以看到，這種變換矩陣使一個向量完全不變：

 

⎡⎣⎢⎢⎢1000010000100001⎤⎦⎥⎥⎥⋅⎡⎣⎢⎢⎢1234⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢1⋅11⋅21⋅31⋅4⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢1234⎤⎦⎥⎥⎥[1000010000100001]⋅[1234]=[1⋅11⋅21⋅31⋅4]=[1234]

向量看起來完全沒變。從乘法法則來看就很容易理解來：第一個結果元素是矩陣的第一行的每個元素乘以向量的每個對應元素。因為每行的元素除了第一個都是0，可得：1⋅1+0⋅2+0⋅3+0⋅4=11⋅1+0⋅2+0⋅3+0⋅4=1，向量的其他3個元素同理。

你可能會奇怪一個沒變換的變換矩陣有什麼用？單位矩陣通常是生成其他變換矩陣的起點，如果我們深挖線性代數，這還是一個對證明定理、解線性方程非常有用的矩陣。

縮放

對一個向量進行縮放(Scaling)就是對向量的長度進行縮放，而保持它的方向不變。由於我們進行的是2維或3維操作，我們可以分別定義一個有2或3個縮放變數的向量，每個變數縮放一個軸(x、y或z)。

我們先來嘗試縮放向量v¯=(3,2)v¯=(3,2)。我們可以把向量沿著x軸縮放0.5，使它的寬度縮小為原來的二分之一；我們將沿著y軸把向量的高度縮放為原來的兩倍。我們看看把向量縮放(0.5, 2)倍所獲得的s¯s¯是什麼樣的：

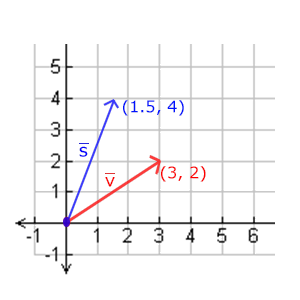
記住，OpenGL通常是在3D空間進行操作的，對於2D的情況我們可以把z軸縮放1倍，這樣z軸的值就不變了。我們剛剛的縮放操作是不均勻(Non-uniform)縮放，因為每個軸的縮放因子(Scaling Factor)都不一樣。如果每個軸的縮放因子都一樣那麼就叫均勻縮放(Uniform Scale)。

我們下面會構造一個變換矩陣來為我們提供縮放功能。我們從單位矩陣瞭解到，每個對角線元素會分別與向量的對應元素相乘。如果我們把1變為3會怎樣？這樣子的話，我們就把向量的每個元素乘以3了，這事實上就把向量縮放3倍。如果我們把縮放變量表示為(S1,S2,S3)(S1,S2,S3)我們可以為任意向量(x,y,z)(x,y,z)定義一個縮放矩陣：

 

⎡⎣⎢⎢⎢S10000S20000S300001⎤⎦⎥⎥⎥⋅⎛⎝⎜⎜⎜xyz1⎞⎠⎟⎟⎟=⎛⎝⎜⎜⎜S1⋅xS2⋅yS3⋅z1⎞⎠⎟⎟⎟[S10000S20000S300001]⋅(xyz1)=(S1⋅xS2⋅yS3⋅z1)

注意，第四個縮放向量仍然是1，因為在3D空間中縮放w分量是無意義的。w分量另有其他用途，在後面我們會看到。

位移

位移(Translation)是在原始向量的基礎上加上另一個向量從而獲得一個在不同位置的新向量的過程，從而在位移向量基礎上移動了原始向量。我們已經討論了向量加法，所以這應該不會太陌生。

和縮放矩陣一樣，在4×4矩陣上有幾個特別的位置用來執行特定的操作，對於位移來說它們是第四列最上面的3個值。如果我們把位移向量表示為(Tx,Ty,Tz)(Tx,Ty,Tz)，我們就能把位移矩陣定義為：

 

⎡⎣⎢⎢⎢⎢100001000010TxTyTz1⎤⎦⎥⎥⎥⎥⋅⎛⎝⎜⎜⎜xyz1⎞⎠⎟⎟⎟=⎛⎝⎜⎜⎜x+Txy+Tyz+Tz1⎞⎠⎟⎟⎟[100Tx010Ty001Tz0001]⋅(xyz1)=(x+Txy+Tyz+Tz1)

這樣是能工作的，因為所有的位移值都要乘以向量的w行，所以位移值會加到向量的原始值上（想想矩陣乘法法則）。而如果你用3x3矩陣我們的位移值就沒地方放也沒地方乘了，所以是不行的。

齊次座標(Homogeneous Coordinates)

向量的w分量也叫齊次座標。想要從齊次向量得到3D向量，我們可以把x、y和z座標分別除以w座標。我們通常不會注意這個問題，因為w分量通常是1.0。使用齊次座標有幾點好處：它允許我們在3D向量上進行位移（如果沒有w分量我們是不能位移向量的），而且下一章我們會用w值建立3D視覺效果。

如果一個向量的齊次座標是0，這個座標就是方向向量(Direction Vector)，因為w座標是0，這個向量就不能位移（譯註：這也就是我們說的不能位移一個方向）。

有了位移矩陣我們就可以在3個方向(x、y、z)上移動物體，它是我們的變換工具箱中非常有用的一個變換矩陣。

旋轉

上面幾個的變換內容相對容易理解，在2D或3D空間中也容易表示出來，但旋轉(Rotation)稍複雜些。如果你想知道旋轉矩陣是如何構造出來的，我推薦你去看可汗學院線性代數的視訊。

首先我們來定義一個向量的旋轉到底是什麼。2D或3D空間中的旋轉用角(Angle)來表示。角可以是角度制或弧度制的，周角是360角度或2 PI弧度。我個人更喜歡用角度，因為它們看起來更直觀。

大多數旋轉函式需要用弧度制的角，但幸運的是角度制的角也可以很容易地轉化為弧度制的：

• 弧度轉角度：角度 = 弧度 * (180.0f / PI)
• 角度轉弧度：弧度 = 角度 * (PI / 180.0f)

PI約等於3.14159265359。

轉半圈會旋轉360/2 = 180度，向右旋轉1/5圈表示向右旋轉360/5 = 72度。下圖中展示的2D向量v¯v¯是由k¯k¯向右旋轉72度所得的：

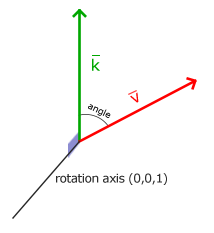
在3D空間中旋轉需要定義一個角和一個旋轉軸(Rotation Axis)。物體會沿著給定的旋轉軸旋轉特定角度。如果你想要更形象化的感受，可以試試向下看著一個特定的旋轉軸，同時將你的頭部旋轉一定角度。當2D向量在3D空間中旋轉時，我們把旋轉軸設為z軸（嘗試想象這種情況）。

使用三角學，給定一個角度，可以把一個向量變換為一個經過旋轉的新向量。這通常是使用一系列正弦和餘弦函式（一般簡稱sin和cos）各種巧妙的組合得到的。當然，討論如何生成變換矩陣超出了這個教程的範圍。

旋轉矩陣在3D空間中每個單位軸都有不同定義，旋轉角度用θθ表示：

沿x軸旋轉：

 

⎡⎣⎢⎢⎢10000cosθsinθ00−sinθcosθ00001⎤⎦⎥⎥⎥⋅⎛⎝⎜⎜⎜xyz1⎞⎠⎟⎟⎟=⎛⎝⎜⎜⎜xcosθ⋅y−sinθ⋅zsinθ⋅y+cosθ⋅z1⎞⎠⎟⎟⎟[10000cos⁡θ−sin⁡θ00sin⁡θcos⁡θ00001]⋅(xyz1)=(xcos⁡θ⋅y−sin⁡θ⋅zsin⁡θ⋅y+cos⁡θ⋅z1)

沿y軸旋轉：

 

⎡⎣⎢⎢⎢cosθ0−sinθ00100sinθ0cosθ00001⎤⎦⎥⎥⎥⋅⎛⎝⎜⎜⎜xyz1⎞⎠⎟⎟⎟=⎛⎝⎜⎜⎜cosθ⋅x+sinθ⋅zy−sinθ⋅x+cosθ⋅z1⎞⎠⎟⎟⎟[cos⁡θ0sin⁡θ00100−sin⁡θ0cos⁡θ00001]⋅(xyz1)=(cos⁡θ⋅x+sin⁡θ⋅zy−sin⁡θ⋅x+cos⁡θ⋅z1)

沿z軸旋轉：

 

⎡⎣⎢⎢⎢cosθsinθ00−sinθcosθ0000100001⎤⎦⎥⎥⎥⋅⎛⎝⎜⎜⎜xyz1⎞⎠⎟⎟⎟=⎛⎝⎜⎜⎜cosθ⋅x−sinθ⋅ysinθ⋅x+cosθ⋅yz1⎞⎠⎟⎟⎟[cos⁡θ−sin⁡θ00sin⁡θcos⁡θ0000100001]⋅(xyz1)=(cos⁡θ⋅x−sin⁡θ⋅ysin⁡θ⋅x+cos⁡θ⋅yz1)

利用旋轉矩陣我們可以把任意位置向量沿一個單位旋轉軸進行旋轉。也可以將多個矩陣複合，比如先沿著x軸旋轉再沿著y軸旋轉。但是這會很快導致一個問題——萬向節死鎖（Gimbal Lock，可以看看這個視訊（優酷）來了解）。在這裡我們不會討論它的細節，但是對於3D空間中的旋轉，一個更好的模型是沿著任意的一個軸，比如單位向量$(0.662, 0.2, 0.7222)$旋轉，而不是對一系列旋轉矩陣進行復合。這樣的一個（超級麻煩的）矩陣是存在的，見下面這個公式，其中(Rx,Ry,Rz)(Rx,Ry,Rz)代表任意旋轉軸：

 

⎡⎣⎢⎢⎢⎢cosθ+Rx2(1−cosθ)RyRx(1−cosθ)+RzsinθRzRx(1−cosθ)−Rysinθ0RxRy(1−cosθ)−Rzsinθcosθ+Ry2(1−cosθ)RzRy(1−cosθ)+Rxsinθ0RxRz(1−cosθ)+RysinθRyRz(1−cosθ)−Rxsinθcosθ+Rz2(1−cosθ)00001⎤⎦⎥⎥⎥⎥[cos⁡θ+Rx2(1−cos⁡θ)RxRy(1−cos⁡θ)−Rzsin⁡θRxRz(1−cos⁡θ)+Rysin⁡θ0RyRx(1−cos⁡θ)+Rzsin⁡θcos⁡θ+Ry2(1−cos⁡θ)RyRz(1−cos⁡θ)−Rxsin⁡θ0RzRx(1−cos⁡θ)−Rysin⁡θRzRy(1−cos⁡θ)+Rxsin⁡θcos⁡θ+Rz2(1−cos⁡θ)00001]

在數學上討論如何生成這樣的矩陣仍然超出了本節內容。但是記住，即使這樣一個矩陣也不能完全解決萬向節死鎖問題（儘管會極大地避免）。避免萬向節死鎖的真正解決方案是使用四元數(Quaternion)，它不僅更安全，而且計算會更有效率。四元數可能會在後面的教程中討論。

譯註

對四元數的理解會用到非常多的數學知識。如果你想了解四元數與3D旋轉之間的關係，可以來閱讀我的教程。如果你對萬向節死鎖的概念仍不是那麼清楚，可以來閱讀我教程的Bonus章節。

現在3Blue1Brown也已經開始了一個四元數的視訊系列，他採用球極平面投影(Stereographic Projection)的方式將四元數投影到3D空間，同樣有助於理解四元數的概念（仍在更新中）：https://www.youtube.com/watch?v=d4EgbgTm0Bg

矩陣的組合

使用矩陣進行變換的真正力量在於，根據矩陣之間的乘法，我們可以把多個變換組合到一個矩陣中。讓我們看看我們是否能生成一個變換矩陣，讓它組合多個變換。假設我們有一個頂點(x, y, z)，我們希望將其縮放2倍，然後位移(1, 2, 3)個單位。我們需要一個位移和縮放矩陣來完成這些變換。結果的變換矩陣看起來像這樣：

 

Trans.Scale=⎡⎣⎢⎢⎢1000010000101231⎤⎦⎥⎥⎥.⎡⎣⎢⎢⎢2000020000200001⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢2000020000201231⎤⎦⎥⎥⎥Trans.Scale=[1001010200130001].[2000020000200001]=[2001020200230001]

注意，當矩陣相乘時我們先寫位移再寫縮放變換的。矩陣乘法是不遵守交換律的，這意味著它們的順序很重要。當矩陣相乘時，在最右邊的矩陣是第一個與向量相乘的，所以你應該從右向左讀這個乘法。建議您在組合矩陣時，先進行縮放操作，然後是旋轉，最後才是位移，否則它們會（消極地）互相影響。比如，如果你先位移再縮放，位移的向量也會同樣被縮放（譯註：比如向某方向移動2米，2米也許會被縮放成1米）！

用最終的變換矩陣左乘我們的向量會得到以下結果：

 

⎡⎣⎢⎢⎢2000020000201231⎤⎦⎥⎥⎥.⎡⎣⎢⎢⎢xyz1⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢2x+12y+22z+31⎤⎦⎥⎥⎥[2001020200230001].[xyz1]=[2x+12y+22z+31]

不錯！向量先縮放2倍，然後位移了(1, 2, 3)個單位。

實踐

現在我們已經解釋了變換背後的所有理論，是時候將這些知識利用起來了。OpenGL沒有自帶任何的矩陣和向量知識，所以我們必須定義自己的數學類和函式。在教程中我們更希望抽象所有的數學細節，使用已經做好了的數學庫。幸運的是，有個易於使用，專門為OpenGL量身定做的數學庫，那就是GLM。

GLM

GLM是OpenGL Mathematics的縮寫，它是一個只有標頭檔案的庫，也就是說我們只需包含對應的標頭檔案就行了，不用連結和編譯。GLM可以在它們的網站上下載。把標頭檔案的根目錄複製到你的includes資料夾，然後你就可以使用這個庫了。

GLM庫從0.9.9版本起，預設會將矩陣型別初始化為一個零矩陣（所有元素均為0），而不是單位矩陣（對角元素為1，其它元素為0）。如果你使用的是0.9.9或0.9.9以上的版本，你需要將所有的矩陣初始化改為 glm::mat4 mat = glm::mat4(1.0f)。如果你想與本教程的程式碼保持一致，請使用低於0.9.9版本的GLM，或者改用上述程式碼初始化所有的矩陣。

我們需要的GLM的大多數功能都可以從下面這3個頭檔案中找到：

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

我們來看看是否可以利用我們剛學的變換知識把一個向量(1, 0, 0)位移(1, 1, 0)個單位（注意，我們把它定義為一個glm::vec4型別的值，齊次座標設定為1.0）：

glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
// 譯註：下面就是矩陣初始化的一個例子，如果使用的是0.9.9及以上版本
// 下面這行程式碼就需要改為:
// glm::mat4 trans = glm::mat4(1.0f)
// 之後將不再進行提示
glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;

我們先用GLM內建的向量類定義一個叫做vec的向量。接下來定義一個mat4型別的trans，預設是一個4×4單位矩陣。下一步是建立一個變換矩陣，我們是把單位矩陣和一個位移向量傳遞給glm::translate函式來完成這個工作的（然後用給定的矩陣乘以位移矩陣就能獲得最後需要的矩陣）。
之後我們把向量乘以位移矩陣並且輸出最後的結果。如果你仍記得位移矩陣是如何工作的話，得到的向量應該是(1 + 1, 0 + 1, 0 + 0)，也就是(2, 1, 0)。這個程式碼片段將會輸出210，所以這個位移矩陣是正確的。

我們來做些更有意思的事情，讓我們來旋轉和縮放之前教程中的那個箱子。首先我們把箱子逆時針旋轉90度。然後縮放0.5倍，使它變成原來的一半大。我們先來建立變換矩陣：

glm::mat4 trans;
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5)); 

首先，我們把箱子在每個軸都縮放到0.5倍，然後沿z軸旋轉90度。GLM希望它的角度是弧度制的(Radian)，所以我們使用glm::radians將角度轉化為弧度。注意有紋理的那面矩形是在XY平面上的，所以我們需要把它繞著z軸旋轉。因為我們把這個矩陣傳遞給了GLM的每個函式，GLM會自動將矩陣相乘，返回的結果是一個包括了多個變換的變換矩陣。

下一個大問題是：如何把矩陣傳遞給著色器？我們在前面簡單提到過GLSL裡也有一個mat4型別。所以我們將修改頂點著色器讓其接收一個mat4的uniform變數，然後再用矩陣uniform乘以位置向量：

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;

out vec2 TexCoord;

uniform mat4 transform;

void main()
{
    gl_Position = transform * vec4(aPos, 1.0f);
    TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
}

GLSL也有mat2和mat3型別從而允許了像向量一樣的混合運算。前面提到的所有數學運算（像是標量-矩陣相乘，矩陣-向量相乘和矩陣-矩陣相乘）在矩陣型別裡都可以使用。當出現特殊的矩陣運算的時候我們會特別說明。

在把位置向量傳給gl_Position之前，我們先新增一個uniform，並且將其與變換矩陣相乘。我們的箱子現在應該是原來的二分之一大小並（向左）旋轉了90度。當然，我們仍需要把變換矩陣傳遞給著色器：

unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));

我們首先查詢uniform變數的地址，然後用有Matrix4fv字尾的glUniform函式把矩陣資料傳送給著色器。第一個引數你現在應該很熟悉了，它是uniform的位置值。第二個引數告訴OpenGL我們將要傳送多少個矩陣，這裡是1。第三個引數詢問我們我們是否希望對我們的矩陣進行置換(Transpose)，也就是說交換我們矩陣的行和列。OpenGL開發者通常使用一種內部矩陣佈局，叫做列主序(Column-major Ordering)佈局。GLM的預設佈局就是列主序，所以並不需要置換矩陣，我們填GL_FALSE。最後一個引數是真正的矩陣資料，但是GLM並不是把它們的矩陣儲存為OpenGL所希望接受的那種，因此我們要先用GLM的自帶的函式value_ptr來變換這些資料。

我們建立了一個變換矩陣，在頂點著色器中聲明瞭一個uniform，並把矩陣傳送給了著色器，著色器會變換我們的頂點座標。最後的結果應該看起來像這樣：

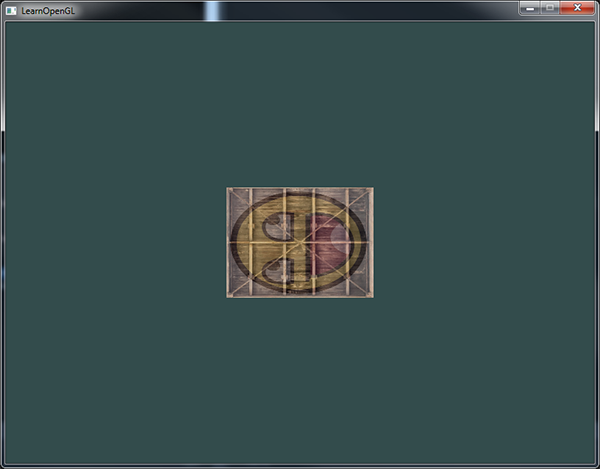
完美！我們的箱子向左側旋轉，並是原來的一半大小，所以變換成功了。我們現在做些更有意思的，看看我們是否可以讓箱子隨著時間旋轉，我們還會重新把箱子放在視窗的右下角。要讓箱子隨著時間推移旋轉，我們必須在遊戲迴圈中更新變換矩陣，因為它在每一次渲染迭代中都要更新。我們使用GLFW的時間函式來獲取不同時間的角度：

glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));

要記住的是前面的例子中我們可以在任何地方宣告變換矩陣，但是現在我們必須在每一次迭代中建立它，從而保證我們能夠不斷更新旋轉角度。這也就意味著我們不得不在每次遊戲迴圈的迭代中重新建立變換矩陣。通常在渲染場景的時候，我們也會有多個需要在每次渲染迭代中都用新值重新建立的變換矩陣

在這裡我們先把箱子圍繞原點(0, 0, 0)旋轉，之後，我們把旋轉過後的箱子位移到螢幕的右下角。記住，實際的變換順序應該與閱讀順序相反：儘管在程式碼中我們先位移再旋轉，實際的變換卻是先應用旋轉再是位移的。明白所有這些變換的組合，並且知道它們是如何應用到物體上是一件非常困難的事情。只有不斷地嘗試和實驗這些變換你才能快速地掌握它們。

如果你做對了，你將看到下面的結果：

這就是我們剛剛做到的！一個位移過的箱子，它會一直轉，一個變換矩陣就做到了！現在你可以明白為什麼矩陣在圖形領域是一個如此重要的工具了。我們可以定義無限數量的變換，而把它們組合為僅僅一個矩陣，如果願意的話我們還可以重複使用它。在著色器中使用矩陣可以省去重新定義頂點資料的功夫，它也能夠節省處理時間，因為我們沒有一直重新發送我們的資料（這是個非常慢的過程）。

如果你沒有得到正確的結果，或者你有哪兒不清楚的地方。可以看原始碼。

下一節中，我們會討論怎樣使用矩陣為頂點定義不同的座標空間。這將是我們進入實時3D影象的第一步！

拓展閱讀

• 線性代數的本質：Grant Sanderson製作的非常棒的視訊教程系列，它討論了變換和線性代數內在的數學本質（中文字幕版本）。

練習

• 使用應用在箱子上的最後一個變換，嘗試將其改變為先旋轉，後位移。看看發生了什麼，試著想想為什麼會發生這樣的事情：參考解答
• 嘗試再次呼叫glDrawElements畫出第二個箱子，只使用變換將其擺放在不同的位置。讓這個箱子被擺放在視窗的左上角，並且會不斷的縮放（而不是旋轉）。（sin函式在這裡會很有用，不過注意使用sin函式時應用負值會導致物體被翻轉）：參考解答