堆排序(heapsort) 像合併排序而不像插入順序，堆排序的執行時間為O(nlgn) 。像插入排序而不像合併排序，它是一種原地( in place) 排序演算法：在任何時候，陣列中只有常數個元素儲存在輸入陣列以外。

堆：

（二叉）堆資料結構是一種陣列物件，它可以被視為一棵完全二叉樹。樹中每個結點與陣列中存放該結點值的那個元素對應。樹的每一層都是填滿的，最後一層可能除外（最後一層從一個結點的左子樹開始填） 。

堆存在以下性質：

根節點：A[1]

父結點：Parent[i] = i/2

左子節點：Left[i] = 2i

右子節點：Right[i] = 2i + 1

陣列長度為：A.length

陣列中有效資料長度為：A.heap-size

堆分為最大堆和最小堆，在最大堆中 Parent[i] >= A[i]，在最小堆中 Parent[i]  <= A[i]

表示堆的陣列A是一個具有兩個屬性的物件：length[A]是陣列中的元素個數， heap-size[A]是存放在A中的堆的元素個數。即雖然A[1. .length[A]]中都可以包含有效值，但A[heap-size [A]]之後的元素都不屬於相應的堆，。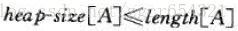

二叉堆有兩種：最大堆和最小堆（小根堆）。在堆排序演算法中，我們使用的是最大堆。最小堆通常在構造優先佇列時使用。

下面幾個是堆排序中的基本過程：

MAX-HEAPITY: 其時間複雜度為O(lgn)， 它是維護最大堆性質的關鍵。

BUILD-MAX-HEAP: 具有線性時間複雜度，功能是從無序的輸入資料陣列中構造一個最大堆。

HEAPSORT: 其時間複雜度為O(nlgn)，功能是對一個數組進行原址排序。

MAX-HEAP-INSERT/HEAP-EXTRACT-MAX/HEAP-INCREASE-KEY/HEAP-MAXIMUM: 時間複雜度為O(nlgn)，功能是利用堆實現一個優先佇列。

維護堆的性質：

MAX-HEAPIFY 是對最大堆進行操作的重要的子程式。調節父結點與子結點位置，使他們滿足最大堆的大小關係。將A[i]的值在最大堆中“逐級下降”，從而使以下標i為根結點的子樹重新遵循最大堆的性質。時間複雜度為O(lgn)。

虛擬碼：

MAX-HEAPIFY(A,i)
l <- Left[i]
r <- Right[i]
if l <= heap-size[A] and A[l] > A[i]
    then largest <- l
    else largest <- i
if r <= heap-size[A] and A[r] > A[lagest]
    then lagest <- r
if i != largest //當根結點不是最大值時
    then exchage A[i] <-> A[lagest]
        MAX-HEAPIFY(A,lagest)
        //交換位置後，以該結點為根的子樹可能違法最大堆的性質，所以需要遞迴呼叫

如：

下圖描述了MAX- HEAPIFY的過程。在演算法的每一步裡，從元素A[i], A[LEFT(i)] 和A[RIGHT(i)] 中找出最大的，並將其下標存在largest 中。如果A[i]是最大的，則以i為根的子樹己是最大堆，程式結束。否則，i的某個子結點中有最大元素，則交換A[i]和A[largest] , 從而使i及其子女滿足堆性質。下標為largest 的結點在交換後的值是A[i] , 以該結點為根的子樹又有可能違反最大堆性質。因而要對該子樹遞迴呼叫MAX- HEAPIFY。

建堆：

建堆（BUILD-MAX-HEAP）：將無序的陣列轉換為最大堆。

虛擬碼：

BUILD-MAX-HEAP(A)
heap-size[A] <- length[A] 
for i <- [length[A]/2] downto 1 
//此處i的值為length[A]/2向下取整的值，因為A[length[A]/2+1...length[A]]為葉子結點，沒有子結點，所以只需考慮前半部分的值  
    do MAX-HEAPIFY(A,i)
    

過程BUILD-MAX-HEAP對樹中的每一個其他結點都呼叫一次MAX-HEAPIFY。時間複雜度為 O(n)。

如：

堆排序演算法：

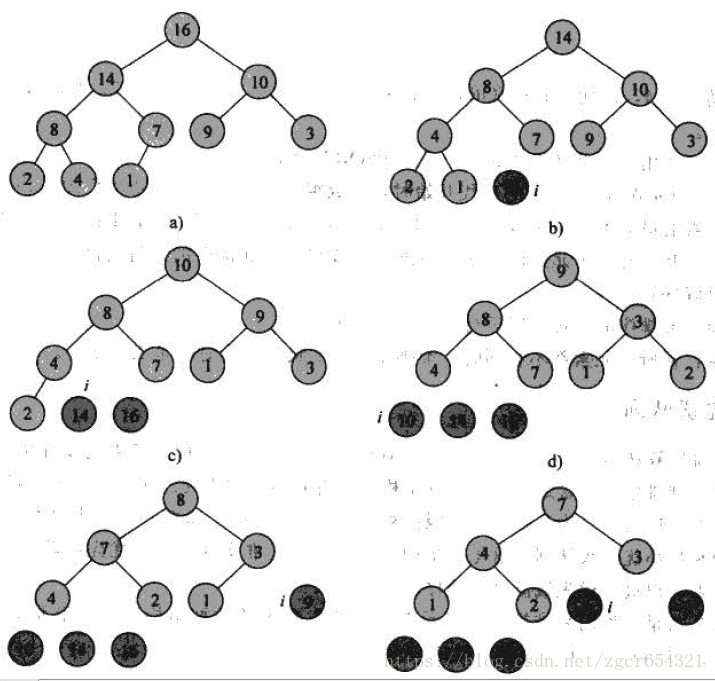
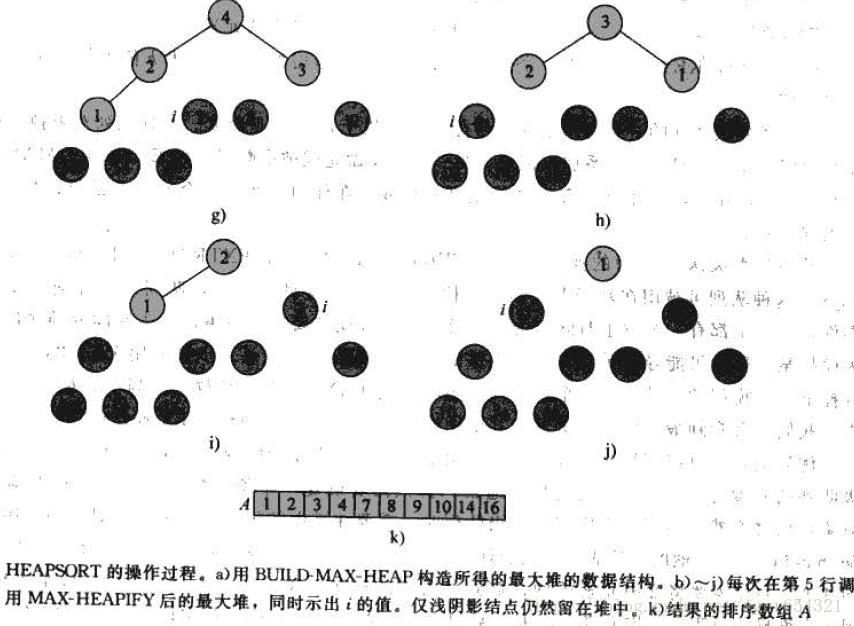
堆排序演算法（HEAPSORT）：建堆後，陣列中的資料並不是有序的，但最大值一定位於根結點A[1]，根據此性質，可以進行排序。時間複雜度為O(nlogn)。

虛擬碼：

HEAPSORT(A)
    BUILD-MAX-HEAP(A)
    for i <- length[A] downto 2 
    //不斷將最大值放在堆中最後一個元素位置，對應就是陣列中由後向前進行排序
        do exchange A[1] <-> A[i] 
        //將最大元素置後
        heap-size[A] <- heap-size[A] - 1 
        //有效長度減1，表示該元素已經歸位
        MAX-HEAPIFY(A,1) 
        //因為將原堆末尾元素提到了根結點，所以需要對根結點重新執行MAX-HEAPIFY維護堆的性質。

如：

優先順序佇列：

優先佇列（priority queue)是一種用來維護由一個元素構成的集合S的資料結構，其中的每一個元素都有一個相關的值，稱為關鍵字(key)，一個最大優先佇列支援以下操作：

INSERT(S, x): 把元素x插入集合S中。

MAXIMUM(S): 返回S中具有最大關鍵字的元素。

EXTRACT-MAX(S): 去掉並返回S中的具有最大關鍵字的元素。

INCREASE-KEY(S, x, k): 將元素x的關鍵字值增加到k，這裡假設k的值不小於x的原關鍵字值。

虛擬碼：

HEAP-MAXIMUM(A)
    return A[1]
HEAD-EXTRACT-MAX(A)
    if heap_size[A]<1
        then error"heap underflow"
    max <- A[1]
    A[1] <- A[heap_size[A]]
    heap_size[A] <- heap_size[A]-1
    MAX-HEAPIFY(A,1)
    return MAX
HEAP-INCREASE-KEY(A, i, key)
    if key<A[i]
        error "new key is smaller than current key"
    A[i] <- key
    while i>1 and A[PARENT(i)]<A[i]
        do exchange A[i] <-> A[PARENT(i)]
            i <- PARENT(i)

MAX-HEAP-INSERT(A, key)
    heap_size[A] <- heap_size[A]+1
    A[heap_size[A]] <- -inf
    HEAP_INCREASE_KEY(A, heap_size[A], key)

程式HEAP-MAXIMUM 用O(1) 時間實現了MAXIMUM 操作。HEAP-EXTRACT-MAX 的執行時間為O(lgn), 因為它除了時間代價為O(lgn) 的MAXHEAPIFY外，只有很少的固定量的工作。

程式HEAP-INCREASE-KEY實現了INCREASE-KEY 操作。在優先順序佇列中，關鍵字值需要增加的元素由對應陣列的下標i來標識。該過程首先將元素A[i] 的關鍵字值更新為新的值。由於增大A[i] 的關鍵字可能會違反最大堆性質，所以過程中採用了類似於INSERTION-SORT的插入迴圈（第5 -7 行）的方式，在從本結點往根結點移動的路徑上，為新增大的關鍵字尋找合適的位置。在移動的過程中，此元素不斷地與其父母相比，如果此元素的關鍵字較大，則交換它們的關鍵字且繼續移動。當元素的關鍵字小於其父母時，此時最大堆性質成立，因此程式終止。

MAX-HEAP-INSERT 實現了INSERT 操作。它的輸入是要插入到最大堆A中的新元素的關鍵字。這個程式首先加入一個關鍵字值為負無窮的葉結點來擴充套件最大堆，然後呼叫HEAP-INCREASE- KEY來設定新結點的關鍵字的正確值，並保持最大堆性質。在包含n個元素的堆上， MAX-HEAP-INSERT 的執行時間為O(lgn) 。

如：

堆排序的程式碼實現：

C/C++程式碼如下：