演算法導論 第十三章:紅黑樹 筆記(紅黑樹的性質、旋轉、插入、刪除)
紅黑樹(red-black tree) 是許多“平衡的”查詢樹中的一種,它能保證在最壞情況下,基本的動態集合操作的時間為O(lgn) 。
紅黑樹的性質:
紅黑樹是一種二叉查詢樹,但在每個結點上增加一個儲存位表示結點的顏色,可以是RED或BLACK 。通過對任何一條從根到葉子的路徑上各個結點著色方式的限制,紅黑樹確保沒有一條路徑會比其他路徑長出兩倍,因而是接近平衡的。
樹中每個結點包含五個域: color, key, left, right和p。如果某結點沒有一個子結點或父結點,則該結點相應的指標(p)域包含值NIL。我們將把這些NIL視為指向二叉查詢樹的外結點(葉子)的指標,而把帶關鍵字的結點視為樹的內結點。
紅黑樹有以下五點性質:
1、每個節點或是紅色的,或是黑色的;
2、根節點是黑色的;
3、每個葉節點(NIL)是黑色的;
4、如果一個節點是紅色的,則其兩個子節點都是黑色的;
5、對於每個節點,從該節點到其所有後代葉節點的簡單路徑上,均包含相同數目的黑色節點。
當滿足以上5個性質的紅黑樹,就能保證沒有一條路徑會比其他路徑長2倍以上,因而可看作近似平衡。
黑高度:
從某個節點x出發到大一個葉節點的任意一條路徑上,黑色節點的個數稱為該節點的黑高度,用bh(x)表示。
以任一結點x為根的子樹至少包含2的bh(x)次方−1個內部結點。
紅黑樹是一種好的二叉查詢樹,對一棵有n個內節點的紅黑樹的高度至多為2lg(n+1),STL中的set和map就是用紅黑樹實現的。紅黑樹的動態集合操作SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR與二叉查詢樹的對應操作的實現一樣,且它們的時間複雜度都是O(lgn)。
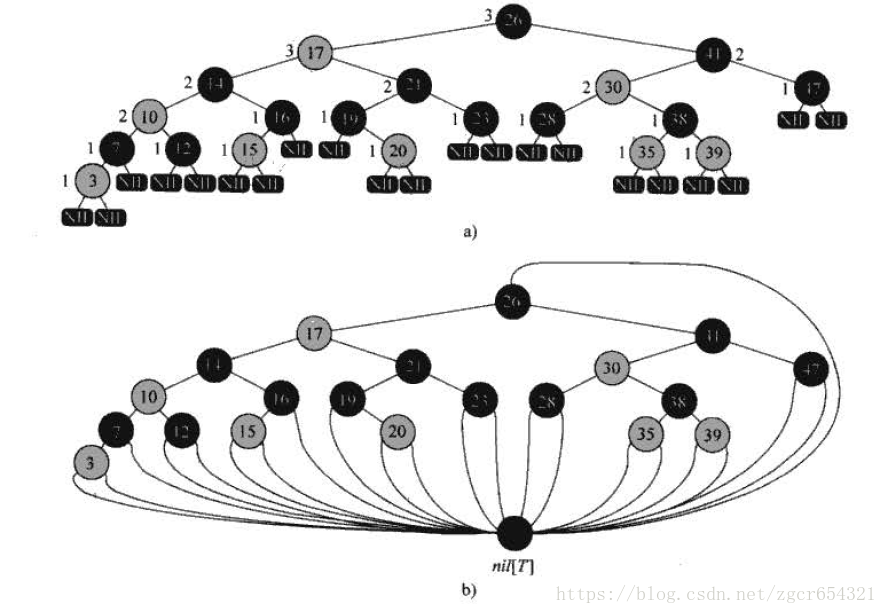
為了便於處理紅黑樹程式碼中的邊界條件,我們採用一個哨兵來代表NIL。對一棵紅黑樹T 來說,哨兵nil[T] 是一個與樹內普通結點有相同域的物件。它的color 域為BLACK, 而它的其他域p, left, right 和key可以設定成任意允許的值。如下圖所示,所有指向NIL的指標都被替換成指向哨兵nil[T]的指標。
使用哨兵後,就可以將結點x的NIL孩子視為一個其父結點為x的普通結點。雖然我們可以在樹內的每一個NIL 上新增一個不同的哨兵結點,來讓每個NIL的父結點都有這樣的定義,但是這種做法會浪費空間。
我們的做法是採用一個哨兵nil[T]來代表所有的NIL——所有的葉子以及根部的父結點。哨兵的域p, left, right 以及key 的取值如何並不重要,為了方便起見,也可以在程式中設定它們。
在本章中,我們使用忽略了所有葉子與根部的父節點的紅黑樹。
如:
旋轉:
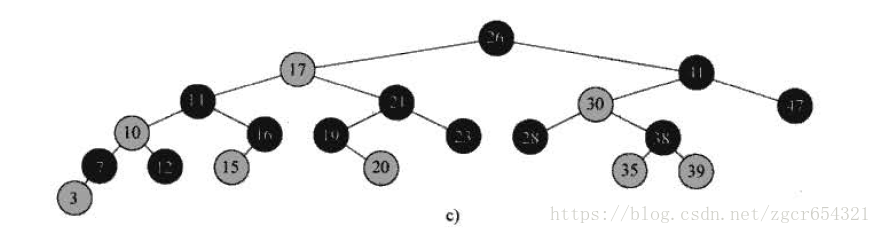
兩種旋轉: 左旋和右旋。
如:
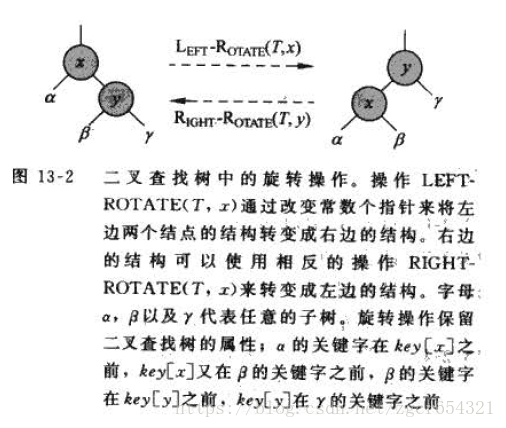
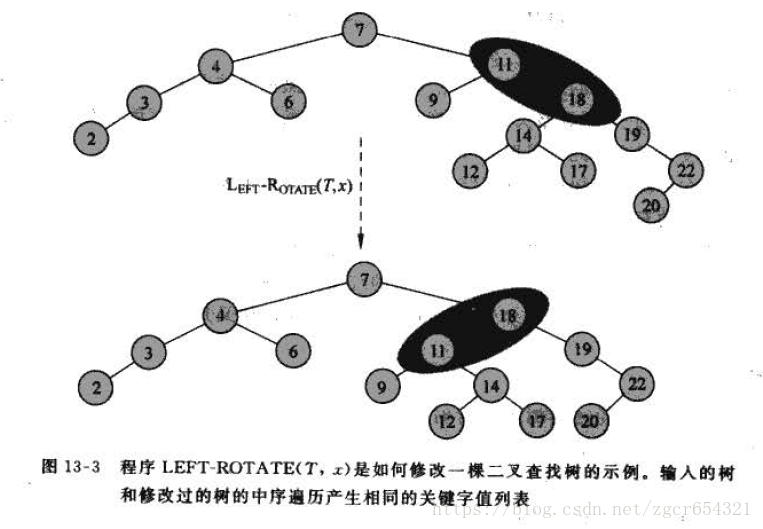
當在某個結點x上做左旋時,我們假設它的右孩子y不是nil[T]; x可以為樹內任意右孩子不是nil[T]的結點。
左旋過後,使y的父結點從x變為x的父結點,x變為y的右子結點,y的左子結點變為x的右子結點。
虛擬碼:
LEFT-ROTATE(T,x)
y <- right[x]
right[x] <- left[y]
if left[y]!= nil[T]
p[left[y]] <- x
p[y] <- p[x]
if p[x] == nil[T]
then root[T] <- y
else if x == left[p[x]]
then left[p[x]] <- y
else right[p[x]] <- y
left[y] <- x
p[x] <- y
RIGHT-ROTATE(T,x)
y <- left[x]
left[x] <- right[y]
if right[y] != nil[T]
p[right[y]] <- x
p[y] <- p[x]
if p[x] == nil[T]
then root[T] <- y
else if x == left[p[x]]
then left[p[x]] <- y
else right[p[x]] <- y
right[y] <- x
p[x] <- y下面舉一個例子:
插入:
向一棵含n 個結點的紅黑樹中插入一個新結點的操作可在O(lgn) 時間內完成。
我們利用TREE-INSERT 過程的一個略作修改的版本,來將結點z插入樹T內,就好像T是一棵普通的二叉查詢樹一樣,然後將z著為紅色。為保證紅黑性質能繼續保持,我們呼叫一個輔助程式RB-INSERT-FIXUP 來對結點重新著色並旋轉。
紅黑樹有以下五點性質:
1、每個節點或是紅色的,或是黑色的;
2、根節點是黑色的;
3、每個葉節點(NIL)是黑色的;
4、如果一個節點是紅色的,則其兩個子節點都是黑色的;
5、對於每個節點,從該節點到其所有後代葉節點的簡單路徑上,均包含相同數目的黑色節點。
z插入後有以下幾種情況:
z作為根節點:(破壞了性質2)修改根節點為黑色即可;
z的父節點為黑色: 不做操作;
z的父節點為紅色:(破壞了性質4)又分成三種情況:
1、z的叔結點y是紅色;
2、z的叔結點y是黑色且z是一個右孩子;
3、z的叔結點y是黑色且z是一個左孩子。
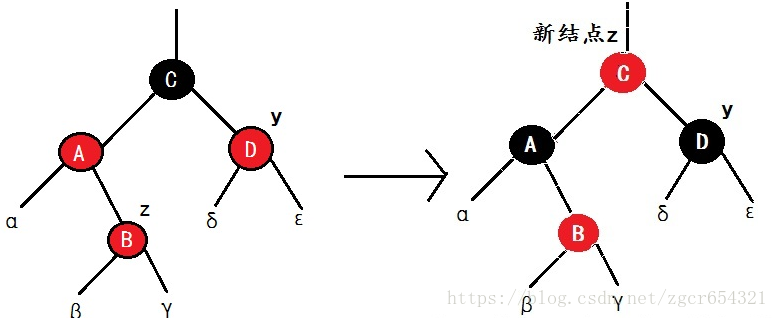
情況1、z的叔結點y是紅色:
如:
如果z的叔節點是紅色,則z結點的祖父結點是黑色,父結點是紅色(父結點和本身都是紅色才會違背性質4)。我們只需要將父、叔結點塗成黑色,祖父結點塗成紅色,而本身顏色不需要改變。
這樣一來只是維護好了自己的“小家庭”,包括父、叔結點和祖父節點。而且保證了性質⑤:紅變黑、黑變紅,並不會增減某一條路徑中黑結點的個數。至於祖父節點的變色可能會導致它和它父親結點的衝突,所以我們就將“當前結點”這個“不合群”的帽子扣在了祖父結點,讓它繼續地被維護。
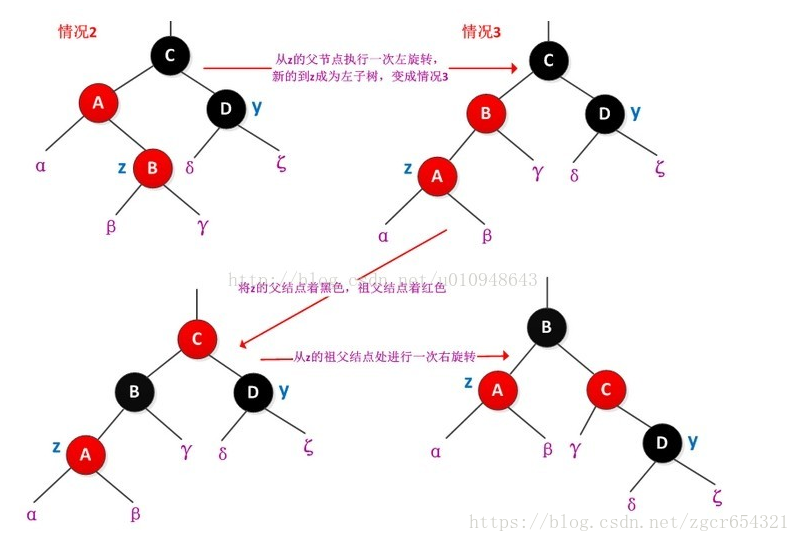
情況2、z的叔結點y是黑色且z是一個右孩子:
將z的父結點做為新的當前結點,將新的當前結點做左旋。這樣就將情況2轉到情況3來處理。
情況3:z的叔結點y是黑色且z是一個左孩子:
如:
如圖,情況2中將z的父結點做為新的當前結點,將新的當前結點做左旋。這樣就變成了情況3。再將此時的z父結點做為新的當前結點,將新的當前結點塗成黑色(之前是紅色),新的當前節點的父節點塗成紅色,再對新的當前結點的父結點做右旋。這樣就保證了性質5,同時修正了性質4,中間並沒有破壞任何其他性質,結束迴圈判斷。
虛擬碼:
RB-INSERT(T,x)
y <- nil[T]
x <- root[T]
while x != nil[T]
do y <- x
if key[z] < key[x]
then x <- left[x]
else x <- right[x]
p[z] <- y
if y == nil[T]
then root[T] <- z
else if key[z] < key[y]
then left[y] <- z
else right[y] <- z
left[z] <- nil[T]
right[z] <- nil[T]
color[z] <- RED
RB-INSERT-FIXUP(T,z)
RB-INSERT-FIXUP(T,z)
while color[p[z]] == RED
do if p[z] == left[p[p[z]]]
then y <- right[p[p[z]]]
if color[y] == RED
then color[p[z]] <- BLACK
color[y] <- BLACK
color[p[p[z]]] <- RED
z <- p[p[z]]
else if z == right[[p[z]]
then z <- p[z]
LEFT-ROTATE(T,x)
color[p[z]] <- BLACK
color[p[p[z]]] <- RED
RIGHT-ROTATE(T,z.p.p)
else(same as then clause with "right" and "left" exchanged)
color[root[T]] <- BLACK刪除:
和n個結點的紅黑樹上的其他基本操作一樣,對一個結點的刪除要花O(lgn) 時間。
程式RB-DELETE是對TREE-DELETE程式略作修改得來的。在刪除一個結點後,該程式就呼叫一個輔助程式RB-DELETE-FIXUP,用來改變結點的顏色並做旋轉,從而保持紅黑樹性質。
刪除操作也分幾個步驟:
首先,按照搜尋二叉樹的刪除操作刪除要刪的結點,然後針對每種情況做換色和旋轉操作,使其恢復紅黑樹的性質。
紅黑樹有以下五點性質:
1、每個節點或是紅色的,或是黑色的;
2、根節點是黑色的;
3、每個葉節點(NIL)是黑色的;
4、如果一個節點是紅色的,則其兩個子節點都是黑色的;
5、對於每個節點,從該節點到其所有後代葉節點的簡單路徑上,均包含相同數目的黑色節點。
換色和旋轉的維護工作分為4種情況考慮(以下情況是x作為其父節點的左孩子的情況,右孩子的情況對稱處理):
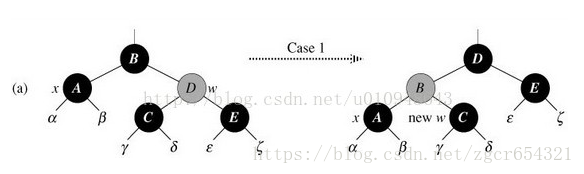
1、待刪結點x的兄弟結點w是紅色:
如圖,x的兄弟結點w是紅色,所以它一定有兩個黑色的子結點。我們只需改變待刪的兄弟結點為黑色,改變父結點的顏色為紅色,然後再對父結點做一次左旋操作,所以待刪結點的兄弟結點一定是黑色。這樣就將情況1轉為情況2、3、4之一去處理。
2、待刪結點x的兄弟結點w是黑色,且w的兩個子結點都是黑色:
如圖,x的兄弟節點w是黑色,且w的兩個子節點都是黑色。這種情況下B左邊黑色高度比右邊的少1,所以只需將w變成紅色就滿足性質5。
如果父節點B本身是黑色的,這時父節點B具有黑黑的屬性,繼續當做x迭代處理!
如果父節點B本身是紅色的,這時父節點B具有紅黑的屬性,直接退出迴圈,把父節點B塗成黑色即可!
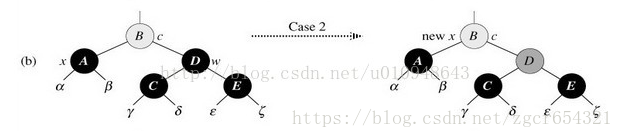
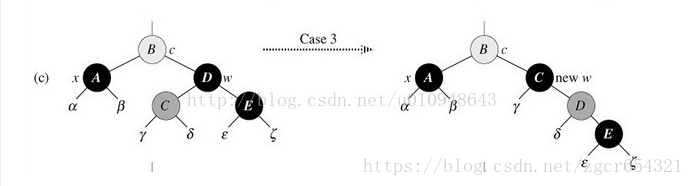
3、待刪結點x的兄弟結點w是黑色,且w的左孩子是紅色,右孩子是黑色:
我們需要交換w和其左孩子的顏色,即C、D顏色互換。然後對w進行右旋,使得待刪結點x的新兄弟結點new w是一個有紅色右孩子的黑色結點,這樣將情況3轉為情況4去處理。
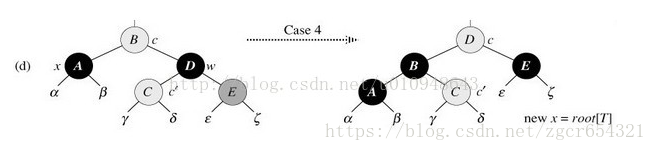
4、待刪結點x的兄弟結點w是黑色,且w的右孩子是紅色:
此時我們可以將兄弟結點D染成當前父結點B的顏色,把當前父結點B的顏色染成黑色,兄弟結點的右子結點E染成黑色。然後對當前父結點B做一次左旋即可。
虛擬碼:
RB-TRANSPLANT(t,u,v)
if u.p == T.nil
T.root = v
else if u == u.p.left
u.p.left = v
else u.p.right = v
v.p = u.p
RB-DELETE(T,z)
y = z
y-original-color = y.color
if z.left == T.nil
x = z.right
RB-TRANSPLANT(T,z,x)
else if z.right == T.nil
x = z.left
RB-TRANSPLANT(T,z,x)
else y = TREE-MINIMUM(z.right)
y-original-color = y.color
x = y.right
if y.p == z
x.p = y
else
RB-TRANSPLANT(T,y,x)
y.right = z.right
z.right.p = y
RB-TRANSPLANT(T,z,y)
y.left = z.left
y.left.p = y
y.color = z.color
if y-original-color == BLACK
RB-DELETE-FIXUP(T,x)
RB-DELETE-FIXUP(T,x)
while x != T.root && x.color == BLACK
if x == x.p.left
w = x.p.right
if w.color == RED
w.color = BLACK
x.p.color = RED
LEFT_ROTATE(T,x.p)
w = x.p.right
if w.left.color == BLACK && w.right.color == BLACK
w.color = RED
x = x.p
else
if w.right.color == BLACK
w.left.color = BLACK
w.color = RED
RIGHT-ROTATE(T,w)
w = x.p.right
w.color = x.p.color
x.p.color = BLACK
w.right.color = BLACK
LEFT_ROTATE(T,x.p)
x = T.root
else(same as then clause with "right" and "left" exchanged)
T.root.color = BLACK