一、引例   1、同學會 　　【例題1】作者有N個同學，並且N個同學中有M對關係，M對關係描述為(a,b)代表a有b的電話號碼(不代表b有a的)。現在作者想舉辦一次同學會，雖然作者有所有人的電話號碼，但是作者這個人比較摳門，不想一個一個打電話浪費電話費。所以如果a能聯絡到b，b能聯絡到c，那麼作者只需要聯絡a（b交給a去聯絡，c交給b去聯絡即可）。聯絡第i個同學的電話費為C[i]。求一種方案使得作者需要消耗的總電話費最少(N<=100000，M<=1000000)。 　　

（思考一分鐘...）
圖一-1-1
最少話費為0，因為直接微信聯絡就可以了，不需要打電話。 哈哈哈哈哈哈哈哈哈哈哈哈！！！！！！！！！
圖一-1-2
　　言歸正傳，我們來仔細分析一下這個問題。把每個同學抽象成圖(Graph)的頂點(Vertex)，如果同學a能夠聯絡到同學b，則建立一條a到b的有向邊(Edge)。那麼，有一些規則是顯而易見的： 　　1)如果圖中某些頂點的入度為0(這個人不能被任何人聯絡到)，肯定只能靠作者自己聯絡了。 　　2)如果構成迴路，那麼只需要聯絡迴路中花費最小（C[i]最小）的那個人，其它人都可以由他來聯絡。
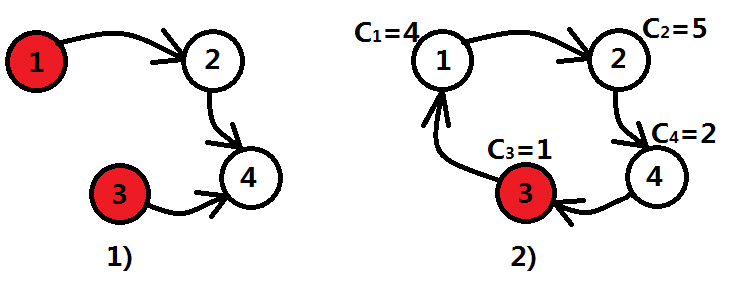
圖一-1-3
兩條規則都比較好理解，第1)條實現比較簡單，建邊的時候就可以統計一個頂點的入度和出度；但是第2)條規則中的迴路就比較模糊了，因為一個點可能屬於多個迴路，如圖一-1-4中，3號結點屬於迴路1->2->3->1，也屬於1->2->3->4->1,同樣也屬於1->2->3->5->1。那麼又產生一個思路：可以將3所在的迴路進行歸併。即圖中1、2、3、4、5這五個結點屬於同一個集合。 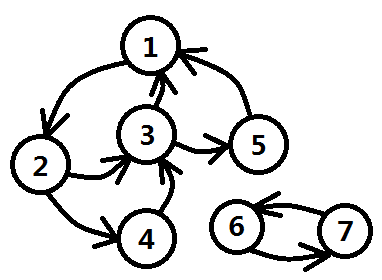圖一-1-4 那麼我們再來看一種情況，如圖一-1-5所示（一個入度為0的點有一條邊指向一個屬於迴路的結點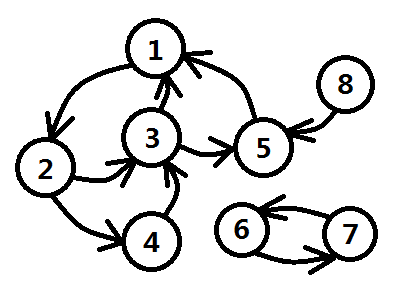）： 圖一-1-5 　　很明顯，這種情況下，1、2、3、4、5這五個結點都可以廢棄不選了，因為8號必選，而選了8，那麼1、2、3、4、5這5個同學都可以通過傳遞性被“聯絡”到。綜上所述，我們大膽假設，如果一個圖是一個有向無環圖（DAG），那麼只需要找出入度為0的點；否則，可以通過將回路消去轉換成DAG圖求解。 　　如圖一-1-6，首先合併迴路1->2->3->1，產生新的結點123（這裡為了通俗易懂所以這麼編號，實際coding過程可以轉換成連續編碼，只要之前沒有出現過的序號均可），並且將新結點的權值C[123]更新為迴路中所有結點的最小值。重複上述步驟，直到整個圖是一個有向無環圖。
圖一-1-6 　　實際編碼起來比較複雜，而且複雜度異常高。我們來分析一下，每次找一條迴路(採用DFS)，最壞複雜度O(N)；將回路中的點進行集合合併（採用並查集)，最壞複雜度為點集個數，也是O(N)；點合併和點集的邊關係需要重新建立，可以做個小技巧，合併後將原先點的進行標記，這樣如果訪問到標記過的點的那條邊就相當於刪除了，建立新邊關係的複雜度和邊數M有關，為O(M)；以上演算法只是進行了一次“縮環”，最壞縮環次數為O(N)，所以整個演算法的時間複雜度為O(N(N+M))，完全無法接受的時間複雜度。 　　所以我們需要順著這個思路繼續往下走，我們來看一個很重要的性質：如果某些點屬於同一個集合，那麼集合中的點必然相互可達，這是由迴路的性質決定的。這就是本文的重點內容-有向圖強連通分量。
二、有向圖強連通
  1、有向圖強連通分量
　　我們可以繼續把這條性質描述為：如果一個有向圖中頂點u能夠通過一些路徑到達頂點v，並且v也可以通過某些路徑到達u，那麼我們說u和v屬於同一個連通分量。當u、v所在集合最大化時，我們說u和v屬於同一個強連通分量。 這裡的強連通分量就是我們之前提到的那個點集合，求強連通分量主要有三個主流演算法，演算法複雜度都是O(V+E)級別的，分別為Kosaraju、Tarjan、Gabow，本文只介紹前兩個，Gabow是對Tarjan的擴充套件，讀者可自行百度。 　　演算法求出的是原頂點到新頂點編號的一個對映，即陣列scc[i]的含義為：原圖中i頂點的強連通分量編號為scc[i]。如圖二-1-1所示的轉換就是原圖到新圖的一個轉化，即縮圖的過程，scc[i]陣列就是一個對映關係，相當於原圖頂點到新圖頂點的對映。 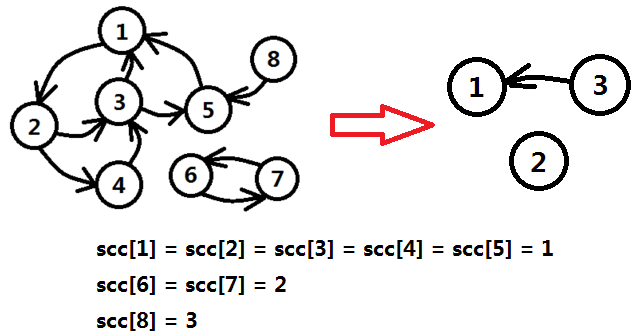圖二-1-1
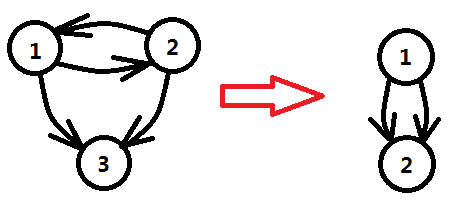
  2、縮圖 　　scc[i]代表了對映關係，然而一個圖只有頂點是不夠的，還需要邊。那麼新圖的邊如何構建呢？ 這一步也非常簡單，直接列舉原圖的所有邊集合，對於邊E(u,v)，分情況討論： 　　　　a)scc[u] !=scc[v]，對新圖建立E(scc[u],scc[v])； 　　　　b )scc[u]==scc[v]，直接忽略這條邊，因為如果建邊E(scc[u],scc[v])，則在新圖中是一個自環，沒什麼意義； 　　這個縮圖的過程，還需要考慮一種情況，如圖所示： 圖二-1-2 　　原本沒有重邊的圖，經過縮圖以後引入了重邊。這種情況，就看實際問題會不會產生影響，如果實際問題對重邊可以自行處理，那麼大可不必理會；否則，可以採用邊雜湊去除重邊。邊雜湊的一般做法就是將兩個頂點壓縮成一個整數然後利用雜湊雜湊。
三、Kosaraju演算法   1、演算法背景
　　Kosaraju演算法是用於求有向圖強連通分量的線性演算法，它有效的利用了一個性質：原圖的強連通分量和反圖的強連通分量一致。演算法主體是基於深度優先搜尋的。關於深搜的詳細內容不再累述，詳情參見《夜深人靜寫演算法》系列的第一篇文章： 　　夜深人靜寫演算法（一）-搜尋入門 　　2、演算法描述 　　資料結構基礎：前向星建邊，建兩張圖：原圖G和反圖G'（反圖即對原圖的每條邊在反圖上建立反向邊）。 　　　　a)對反圖G'求一次後序遍歷，按照遍歷完畢的先後順序將所有頂點記錄在陣列order中。 　　　　b)按照order陣列的逆序，對原圖G求一次先序遍歷，標記連通分量。 　　演算法描述就是這麼簡單，接下來我們進行精密的演算法剖析。 　　3、演算法剖析
　　　　a.反圖的後序遍歷 　　　　第一步，先把圖建出來，可以利用C++中的STL的vector來存邊，也可以自己實現連結串列。
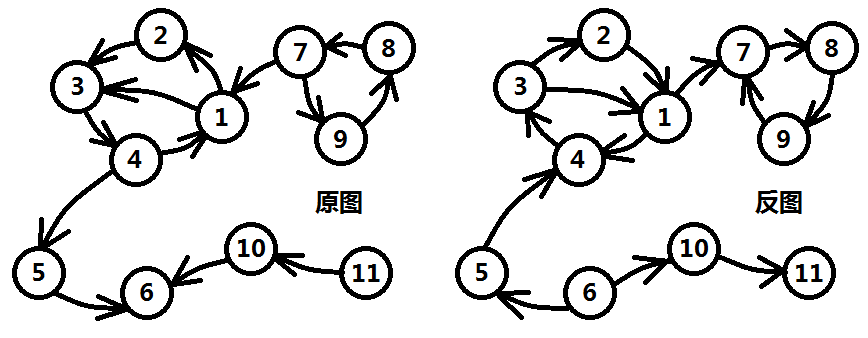
圖三-3-1 　　對反圖G'求一次後序遍歷，按照遍歷完畢的先後順序將頂點記錄在陣列order中。那麼對於圖三-3-1所示的這張反圖，後序遍歷的結果陣列如下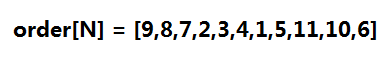： 圖三-3-2 　　這個陣列的下標的含義是時間戳，表示的是它和它鄰接的結點都被訪問完畢的時間。後序遍歷保證每個結點只訪問一次。 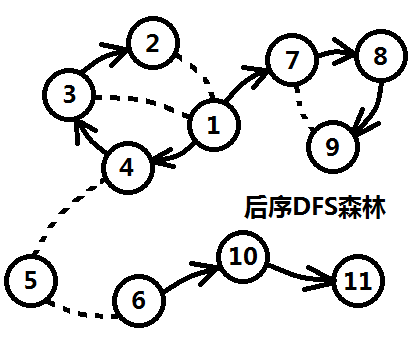圖三-3-3 　　由於每個結點只訪問一次，所以如果後序遍歷的時候出現了環，那條回邊是忽略的，所以無論原先的圖是什麼，後序遍歷，遍歷得到的結果是一個森林 （如圖三-3-3所示，虛線代表回邊，不會被遍歷到）。 這個反圖的後序遍歷結果是三棵樹，根結點分別為1、5、6。並且根結點的時間戳在它所在的樹中一定是最大的。 （顯然，如果原圖是一個DAG圖，那麼後序遍歷逆向圖G'，求出的order正好是一個原圖的拓撲排序，參考原圖中的11->10->6）。 　　　b.原圖的先序遍歷 　　　　第二步，按照order的反向順序，對原圖求一次先序遍歷。標記連通塊。 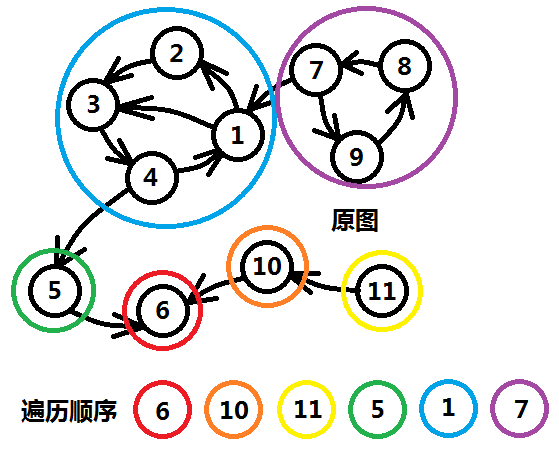圖三-3-4 圖三-3-5
　　兩次DFS的時間複雜度均為O(V+E),而且實現起來非常簡單。那麼，究竟 為什麼可以這樣求強連通分量？ 　　定義：從強連通分量的定義出發，如果兩個頂點a和b，a能夠到b，b也能夠到a，則a和b屬於同一個強連通。 對反圖上的兩個點a和b，如果a能夠到b，則a的時間戳大於b，b屬於a的DFS樹中的子孫結點。 那麼如果在原圖中，a也能夠到b，則說明在反圖中b能夠到a，又由於原圖和反圖的強連通一致，所以a和b屬於同一個強連通。 那麼現在就是要給定a，找出所有能夠到達的b。 　　用a->b來表示在搜尋樹上，a是b的祖先結點，b是a的子孫結點。 　　由於第二次遍歷是時間戳大的頂點開始遍歷，遍歷完標記，所以a能夠到達的點的時間戳一定是小於a的時間戳的（大於a時間戳的頂點已經在逆序訪問的時候先被標記掉了），令到達的點為b，則b在反圖上和a的關係為a->b，這是利用了時間戳的相對大小來確定誰是誰的子孫結點。那麼原圖a->b，反圖也是a->b，所以a和b屬於同一個強連通，得證。 這個演算法可以說是最簡單的演算法了，但是理解起來真的有難度。 Kosaraju演算法的C++實現
四、Tarjan演算法   1、演算法背景
　　Tarjan演算法利用了棧的性質，可以在O(V+E)的線性時間內求出有向圖的強連通分量。由於只需要一次深度優先遍歷，所以無論在演算法時間複雜度，還是編碼複雜度上，都優於Kosaraju演算法。 　　2、演算法描述 　　資料結構基礎： 　　　　　　棧　　　　　　　　stack[top]　　　　儲存正在進行遍歷的結點 　　　　　　時間戳陣列　　　　　　dfn[u]　　　　結點u第一次被遍歷到的時間戳（實際上，每個結點也只會被遍歷一次） 　　　　　　追溯陣列　　　　　　low[u]　　　　　在遍歷時，結點u能夠追溯到的祖先結點中時間戳最小的值
　　　　a)對所有未被標記的結點u 呼叫Tarjan(u) 。 　　　　b)Tarjan(u)是一個深度優先搜尋 　　　　　　1)標記dfn[u]和low[u]為當前時間戳，將u入棧； 　　　　　　2)訪問和u鄰接的所有結點v； 　　　　　　　　如果v未被訪問，則遞迴呼叫Tarjan(v)，呼叫完畢更新low[u]=min{low[u],low[v]}; 　　　　　　　　如果v在棧中，則更新low[u]=min{low[u],dfn[v]}; 　　　　　　3）u鄰接結點均訪問完畢，如果dfn[u]和low[u]相等，則當前棧中所有結點屬於同一個強連通分量，標記scc陣列； 　　這個演算法比較容易理解，難點在於第2)步的最小值更新，low和dfn容易搞混。不過沒事，接下來還是進行一輪精密的演算法剖析。 　　3、演算法剖析   快速過一遍Tarjan演算法，加深對 dfn陣列和low陣列的理解 （白色結點為尚未訪問的結點；彩色結點為正在訪問的結點，並且一定在棧中；灰色結點為訪問完畢的結點）。   首先，從1號結點出發，將沒有訪問過的結點按照深度優先搜尋的順序依次遍歷，遍歷順序為1=>3=>4，時間戳陣列dfn和追溯陣列low分別在訪問結點入口更新，元素依次入棧，棧中元素為{1,3,4}。
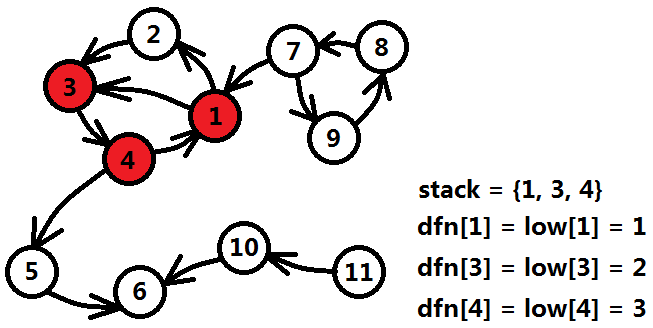
  接著，4號結點繼續擴充套件，發現5號結點；5號結點擴充套件發現6號結點，同樣沒有發現什麼異樣，棧中元素{1,3,4,5,6}。
  這時，6號結點發現自己沒有出邊，並且dfn[6] == low[6]，說明6是一個獨立的強連通分量，標記6的強連通編號為1（圖中的sccID為強連通編號的對映），將6出棧，6的使命完成了，可以置灰了。
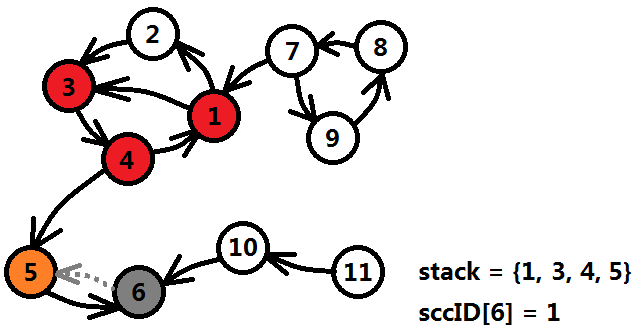
  6號結點回溯到5號結點時（灰色虛線代表回溯），low[5]=min{low[5],low[6]}=4，然後5號結點發現沒有其它的邊可以遍歷，並且dfn[5]==low[5]，說明5也是一個獨立的強連通分量，標記5的強連通編號為2，將5出棧並置灰。   5號結點回溯到4號，沒有發生任何事情。
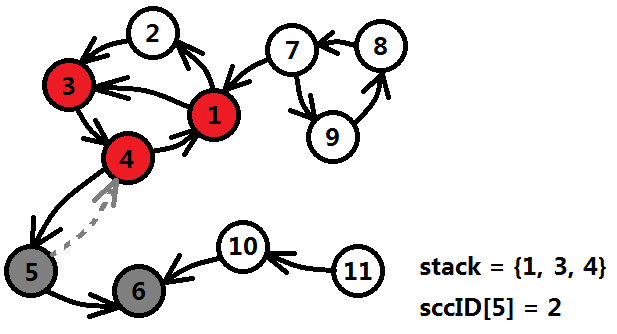
  但是當4號繼續遍歷它剩餘的邊時，發現了連到1號結點的邊（圖中藍色箭頭），這時1號結點還在棧中，也就是1和4必定形成了一個環，那麼它們肯定在同一個強連通分量中，更新4號結點的追溯陣列low[4]=min{low[4],dfn[1]}=1。   當4號結點的出邊都訪問完畢後，low[4]不等於dfn[4]，說明4號結點所在的強連通分量的根還在棧中，先不急，不作任何操作。
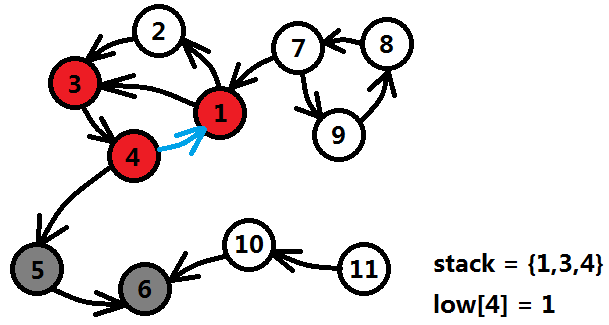
  4號結點回溯到3號結點，更新low[3]；3號結點回溯到1號結點，更新low[1]。
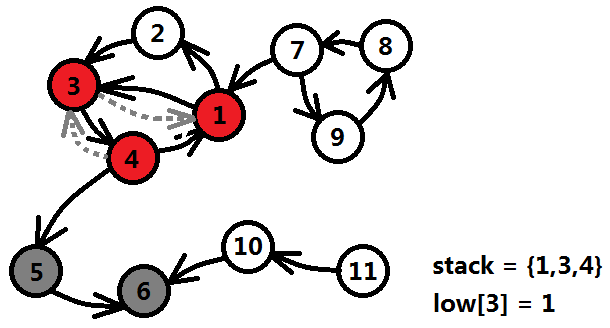
  1號結點遍歷剩餘的邊發現2號結點尚未遍歷，則擴充套件2號，並且將2號結點入棧，時間戳為6。
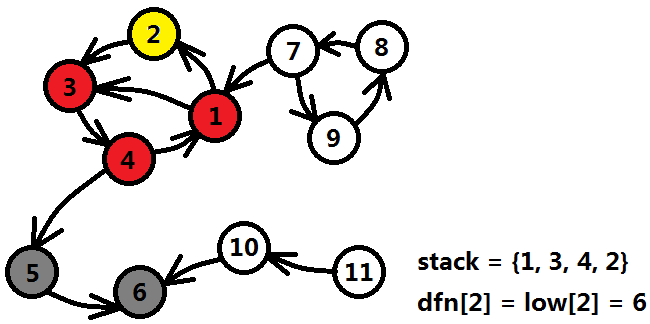
  2號結點遇到了和4號結點一樣的情況，還是用藍色箭頭表示它遇上了一個棧中的結點，即3號，3號還沒有置灰，說明3號一定能夠直接或者間接的訪問到2號的祖先，更新low[2]=min{low[2],dfn[3]}=2。
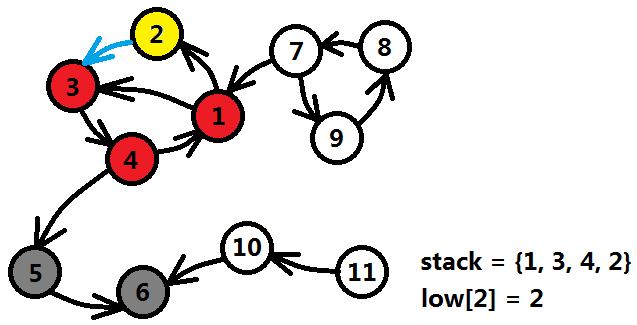
  2號結點回溯到1號結點，1號結點發現沒有任何剩餘邊可以遍歷後退出迴圈，然後判斷dfn[1]==low[1]，終極大BOSS終於出現了，將棧中的元素{1,3,4,2}全部出棧，並且標記這些點的強連通編號為3，結點置灰。
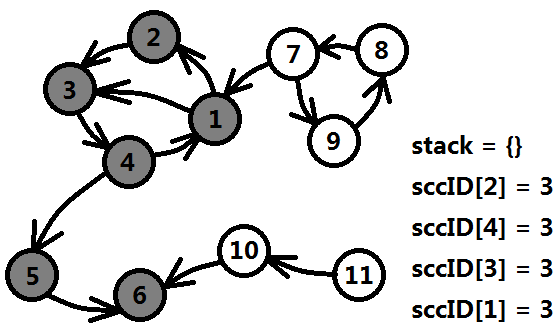
  這時我們發現，本次遞迴已經結束，但是還有白色結點尚未訪問。所以Tarjan演算法需要在外層套一層輪詢，判斷每個結點是否被訪問，將未被訪問的結點作為搜尋樹的樹根，標記已訪問，並且執行Tarjan演算法。 　　最後獻上: Tarjan演算法的C++實現

五、2-sat問題 　　【例題2】 給定一些邏輯關係式X　op　Y　=　Z。其中op的取值為(AND,OR,XOR),X,Y,Z的取值為[0,1]，其中X和Y為未知數，給定未知數和關係式的個數(N,M<100000)，求是否存在這樣一種解滿足所有關係式，存在輸出YES,否則NO。 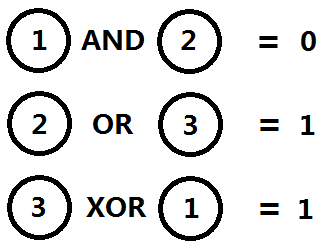圖五-1 　　如圖五-1所示，表示X[1]&X[2]=0；X[2]|X[3]=1；X[3]^X[1]=1；那麼我們能夠肉眼看出來，只要當X[1]=0；X[2]=1；X[3]=1;滿足三個方程都成立。那麼當未知數和方程茫茫多的時候，我們肉眼就無能為力了。只能靠計算機。
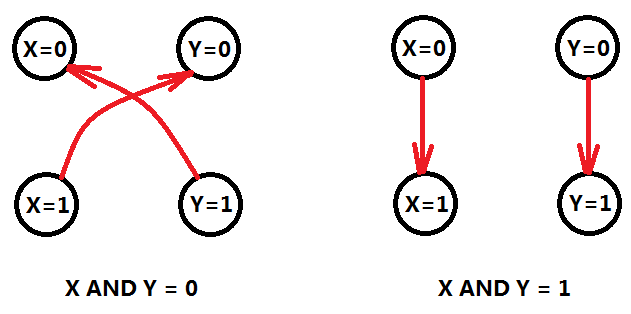
　　樸素演算法是列舉，因為每個數的取值只有兩種，所以可以列舉每個數是0還是1，然後判斷它所在的所有等式中是否滿足條件，這個列舉的開銷是非常大的，因為每個數都有兩種情況，所以總的時間複雜度勢必為O(2^N)。 　　對於這類問題，我們可以利用數形結合，將這個數字問題轉化成圖論問題。 　　1、數形結合 　　首先來看X AND Y，對於這樣一個邏輯表示式，我們可以得出這樣一個事實： 　　　　a)X　AND　Y=0，可以得出：如果X為1，則Y必定為0；同理，如果Y為1，則X必定為0； 　　　　b)X　AND　Y=1，可以得出：X和Y都為1；我們還可以這樣說：如果X為0，則X為1；同理，如果Y為0，則Y為1； 　　基於上面兩條，我們將每個變數拆成兩個點，一個點表示X=0的情況，一個點表示X=1的情況。 圖五-2
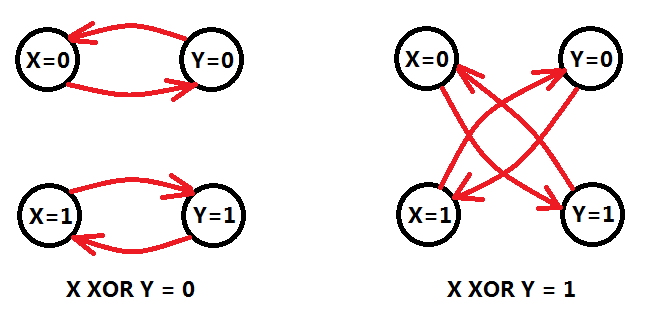
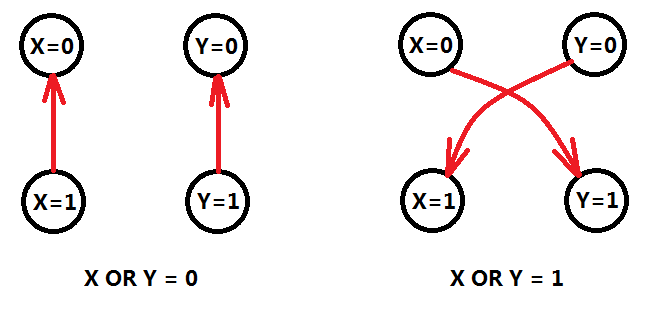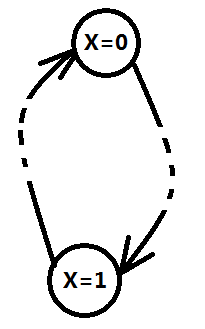
　　如圖五-2，對於X AND Y = 0的情況，如果X=1則Y=0，建立有向邊(X=1)=>(Y=0)，同理(Y=1)=>(X=0)。那麼X AND Y = 1的情況，也採用類似的方法建立有向邊。 然後我們發現OR和XOR也可以採用類似的方法，建立有向邊。 圖五-3 圖五-4 　　將上述每個等式按照這些規則建立有向邊，然後求一次強連通分量。然後一次線性掃描，判斷某個點X的兩種取值(X=0)和(X=1)如果在同一個強連通分量，則等式組無解，否則必定存在至少一組解。
　　正確性很容易理解，如圖五-5所示，還是從定義出發，X=0和X=1位於同一個強連通，則說明當X=0時，可以通過一些步驟推匯出X=1；並且當X=1時，又可以推匯出X=0；這顯然和事實不符。 圖五-5 　　2、蘊含式推導 　　最後給出OR關係式的更加嚴謹的數學推導。
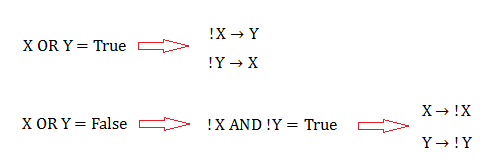
圖五-2-1 六、強連通分量相關題集整理

強連通分量相關
迷宮城堡 ProvingEquivalences
EquivalentSets
IntelligenceSystem Cactus
SummerHoliday
2-sat相關 Party
Wedding KatuPuzzle
PerfectElection PriestJohn'sBusiestDay Ikki'sStoryIV-Panda'sTrick GetLuffyOut GetLuffyOut* Buildingroads GoDeeper EliminateT heConflict BombGame DivideGroups MapLabeler
Let'sgohome PeacefulCommission