在圖論中，一個有向圖被成為是強連通的（strongly connected）當且僅當每一對不相同結點u和v間既存在從u到v的路徑也存在從v到u的路徑。有向圖的極大強連通子圖（這裡指點數極大）被稱為強連通分量（strongly connected component）。

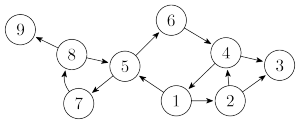
比如說這個有向圖中，點\(1,2,4,5,6,7,8\)和相應邊組成的子圖就是一個強連通分量，另外點\(3,9\)單獨構成強連通分量。

Tarjan演算法是由Robert Tarjan提出的用於尋找有向圖的強連通分量的演算法。它可以在\(O(|V|+|E|)\)的時間內得出結果。

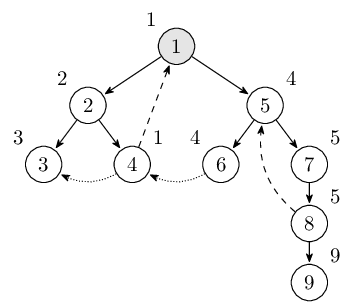
Tarjan演算法主要是利用DFS來尋找強連通分量的。在介紹該演算法之前，我們先來介紹一下搜尋樹。先前那個有向圖的搜尋樹是這樣的：

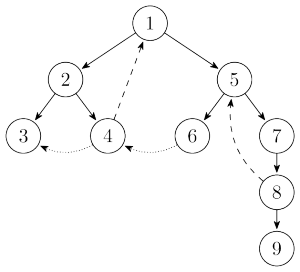
有向圖的搜尋樹主要有\(4\)種邊（這張圖只有\(3\)種），其中用實線畫出來的是樹邊（tree edge），每次搜尋找到一個還沒有訪問過的結點的時候就形成了一條樹邊。用長虛線畫出來的是反祖邊（back edge），也被叫做回邊。用短虛線畫出來的是橫叉邊（cross edge），它主要是在搜尋的時候遇到了一個已經訪問過的結點，但是這個結點並不是當前節點的祖先時形成的。除此之外，像從結點\(1\)到結點\(6\)這樣的邊叫做前向邊（forward edge），它是在搜尋的時候遇到子樹中的結點的時候形成的。

現在我們來看看在DFS的過程中強連通分量有什麼性質。

很重要的一點是如果結點u

Tarjan演算法主要是在DFS的過程中維護了一些資訊：DFN、LOW和一個棧。

• 棧裡的元素表示的是當前已經訪問過但是沒有被歸類到任一強連通分量的結點。
• \(DFN[u]\)表示結點u在DFS中第一次搜尋到的次序，通常被叫做時間戳。
• \(LOW[u]\)稍微有些複雜，它表示從u或者以u為根的子樹中的結點，再通過一條反祖邊或者橫叉邊可以到達的時間戳最小的結點v的時間戳，並且要求v有一些額外的性質：v還要能夠到達u。顯然通過反祖邊到達的結點v滿足LOW的性質，但是通過橫叉邊到達的卻不一定。

可以證明，結點u是某個強連通分量的根等價於\(DFN[u]\)和\(LOW[u]\)相等。簡單可以理解成當它們相等的時候就不可能從u通過子樹再經過其它時間戳比它小的結點回到u。

當通過u搜尋到一個新的節點v的時候可以有多種情況：

1. 結點u通過樹邊到達結點v。

   \(LOW[u]=\min(LOW[u],LOW[v])\)

2. 結點u通過反祖邊到達結點v，或者通過橫叉邊到達結點v並且滿足LOW定義中v的性質，

   \(LOW[u]=\min(LOW[u],DFN[v])\)

在Tarjan演算法進行 DFS的過程中，每離開一個結點，我們就判斷一下LOW是否小於DFN，如果是，那麼著個結點可以到達它先前的結點再通過那個結點回到它，肯定不是強連通分量的根。如果DFN和LOW相等，那麼就不斷退棧直到當前結點為止，這些結點就屬於一個強連通分量。

至於如何更新LOW，關鍵就在於第二種情況，當通過反祖邊或者橫叉邊走到一個結點的時候，只需要判斷這個結點是否在棧中，如果在就用它的LOW值更新當前節點的LOW值，否則就不更新。因為如果不在棧中這個結點就已經確定在某個強連通分量中了，不可能回到u。

現在我們對著先前的圖模擬一次。結點內的標號就是DFN值，結點邊上的標號是表示LOW值，當前所在的結點用灰色表示。

首先從第一個結點開始進行搜尋，最初LOW[1]=1。此時棧裡的結點是\(1\)。

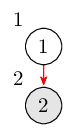
然後到達第二個結點，同時也初始化LOW[2]=2。此時棧裡的結點是\(1,2\)。

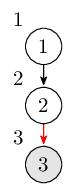
類似地，到達第三個結點，同時也初始化LOW[3]=3。此時棧裡的結點是\(1,2,3\)。

此時結點3沒有其餘邊可以繼續進行搜尋了，我們需要離開它了，因為發現DFN[3]=LOW[3]，所以結點3是一個強連通分量的根，出棧直到結點3為止，得到剛好只有一個結點3的強連通分量。此時棧裡的結點是\(1,2\)。

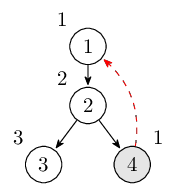
從結點3返回後到結點2，而後進入結點4，從結點4可以到達結點1，但是結點1已經訪問過了，並且是通過反祖邊，更新LOW[4]的值。此時棧裡的結點是\(1,2,4\)。

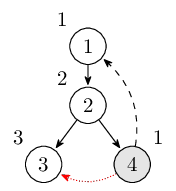
繼續從結點4還可以通過橫叉邊到達結點3，但是結點3並不在棧中（也就是結點3並沒有路徑到達結點4），不做任何改動。此時棧裡的結點是\(1,2,4\)。

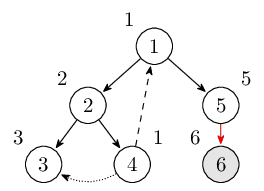
接著一直搜尋直到結點6。此時棧裡的結點是\(1,2,4,5,6\)。

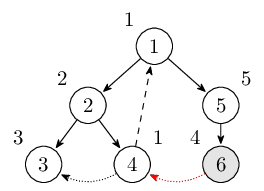
從結點6出發可以通過橫叉邊到達結點4，因為它已經訪問過而且還在棧中，更新LOW[6]。此時棧裡的結點是\(1,2,4,5,6\)。

接著回退到結點5，使用結點6的值更新LOW[5]。此時棧裡的結點是\(1,2,4,5,6\)。

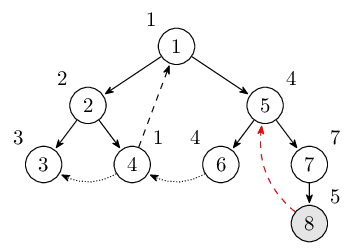
從結點5出發經過結點7後到達結點8。遇到反祖邊回到結點5更新LOW[8]。此時棧裡的結點是\(1,2,4,5,6,7,8\)。

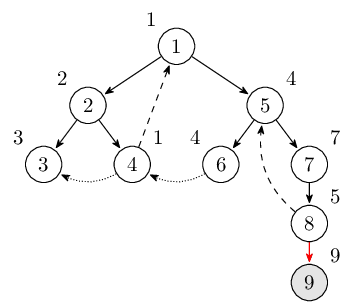
繼續到達結點9。此時棧裡的結點是\(1,2,4,5,6,7,8,9\)。

離開時發現DFN[9]=LOW[9]。找到強連通分量，出棧。此時棧裡的結點是\(1,2,4,5,6,7,8\)。

回到結點8，此時LOW[8]<DFN[8]，不做處理繼續回退。

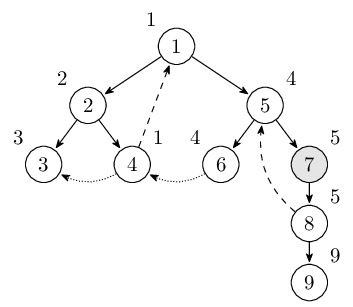
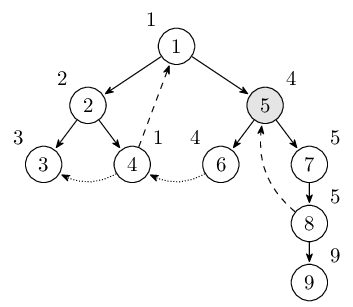
直到回到結點1的時候LOW[1]=DFN[1]。此時棧裡的結點是\(1,2,4,5,6,7,8\)。一直退棧直到遇見1，找到強連通分量\(1,2,4,5,6,7,8\)。

程式碼實現：

inline void tarjan(int u) {
    DFN[u]=LOW[u]=++Time;//Time表示時間戳
    stack[u]=1;//stack[u]表示結點u是否仍然在棧中
    stack[top++]=u;//top表示棧頂位置
    for (int k=head[u]; k; k=next[k])
    {
        int v=point[k];
        if (!DFN[v]) {//樹邊的情況
            tarjan(v);
            if (LOW[v]<LOW[u]) LOW[u]=LOW[v];
        } else if(stack[v] && DFN[v]<LOW[u]) LOW[u]=DFN[v];//橫叉邊或者反祖邊的情況
    }
    if (LOW[u]==DFN[u]) {
        ++cnt;//表示強連通分量的個數
        tmp=0;
        while (tmp!=u) {
            tmp=stack[--top];
            belong[tmp]=cnt;//belong[u]表示結點u屬於那一個強連通分量
            stack[tmp]=0;
        }
    }
}