夜深人靜寫演算法(十一)- 最小包圍球
阿新 • • 發佈:2018-12-05
 一、前言
1、空間點集的最小包圍球
【例題1】三維空間中N(N <= 1000000)個點的集合,需要求一個球體包圍所有的點,並且半徑最小。演算法要求給出這個球體的球心和半徑大小。
一、前言
1、空間點集的最小包圍球
【例題1】三維空間中N(N <= 1000000)個點的集合,需要求一個球體包圍所有的點,並且半徑最小。演算法要求給出這個球體的球心和半徑大小。
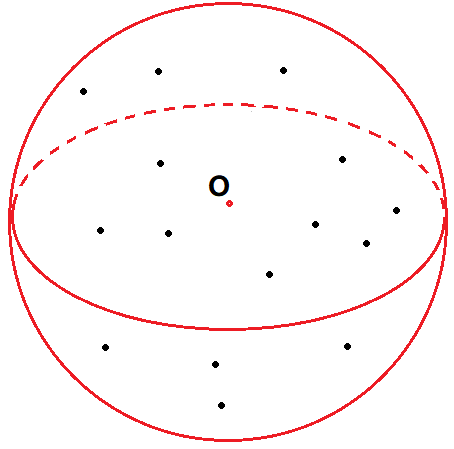
圖一-1-1 最小包圍球在計算幾何、碰撞檢測、人工智慧以及模式識別等領域都有著廣泛應用。計算機圖形學中,三維空間點集的最小包圍球相比三維凸包而言,可以更加快速且精確的進行碰撞檢測。而這些領域中點集的資料量往往是巨大的,所以快速有效的求解最小包圍球的演算法就顯得尤為重要。
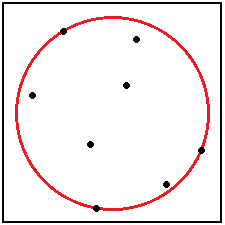
圖一-2-1 兩者看起來是類似的問題,然而當我們思考空間問題沒有頭緒的時候,往往可以採用降維的思想,將空間問題轉化成平面問題,然後再回到空間問題。那麼,接下來本文將循序漸進,將求解最小覆蓋圓的演算法從O(n^4)優化到O(n^3)、再優化到O(n^2)。最後推翻之前的一切引入一個O(n)的演算法。 介紹演算法之前,首先來看一個概念,也是本文的核心演算法,即隨機增量演算法。
 圖三-1-1
2、O(n^3)演算法
對以上思路進行一個優化,我們知道最小覆蓋圓必然至少經過兩個點(除非原點集一共只有一個點)。列舉任意兩個點作為最小覆蓋圓的一條弦,那麼圓心必然在兩點的中垂線上,如圖三-2-1。這個覆蓋圓有三種情況:
圖三-1-1
2、O(n^3)演算法
對以上思路進行一個優化,我們知道最小覆蓋圓必然至少經過兩個點(除非原點集一共只有一個點)。列舉任意兩個點作為最小覆蓋圓的一條弦,那麼圓心必然在兩點的中垂線上,如圖三-2-1。這個覆蓋圓有三種情況:
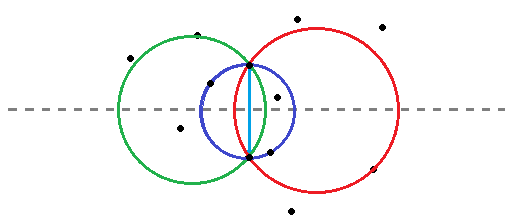 圖三-2-1
a、圓心為這兩點的中點(藍色圓);
b、圓心落在弦的左邊(綠色圓);
c、圓心落在弦的右邊(紅色圓);
圖三-2-1
a、圓心為這兩點的中點(藍色圓);
b、圓心落在弦的左邊(綠色圓);
c、圓心落在弦的右邊(紅色圓);
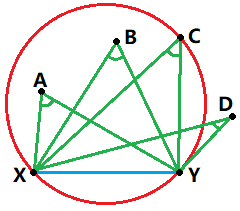 圖三-2-2
如圖三-2-2所示,藍色線段XY代表圓上的弦,其餘的點和絃上兩點XY構成夾角(如圖中的∠XAY、∠XBY、∠XCY、∠XDY),夾角的關係為:圓外角<圓周角<圓內角,所以要覆蓋所有的點,必然要讓這個夾角最小。那麼只要遍歷所有的點,找出夾角最小的這個點,三點確定一個圓。然後再判斷其餘的點是否在這個找到的圓內,列舉任意一條弦的複雜度O(n^2),尋找夾角最小的點和判定是否在圓內是分開的操作,複雜度分別為O(n),所以總時間複雜度O(n^3)。
3、O(n)演算法
最後介紹一個平均期望O(n)的演算法。
1)隨機增量法,打亂所有點的順序。
圖三-2-2
如圖三-2-2所示,藍色線段XY代表圓上的弦,其餘的點和絃上兩點XY構成夾角(如圖中的∠XAY、∠XBY、∠XCY、∠XDY),夾角的關係為:圓外角<圓周角<圓內角,所以要覆蓋所有的點,必然要讓這個夾角最小。那麼只要遍歷所有的點,找出夾角最小的這個點,三點確定一個圓。然後再判斷其餘的點是否在這個找到的圓內,列舉任意一條弦的複雜度O(n^2),尋找夾角最小的點和判定是否在圓內是分開的操作,複雜度分別為O(n),所以總時間複雜度O(n^3)。
3、O(n)演算法
最後介紹一個平均期望O(n)的演算法。
1)隨機增量法,打亂所有點的順序。
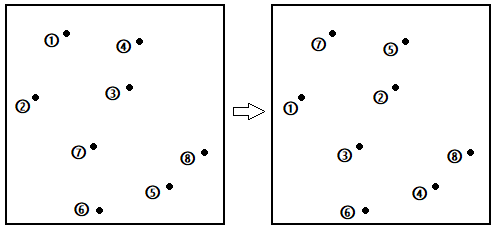 圖三-3-1
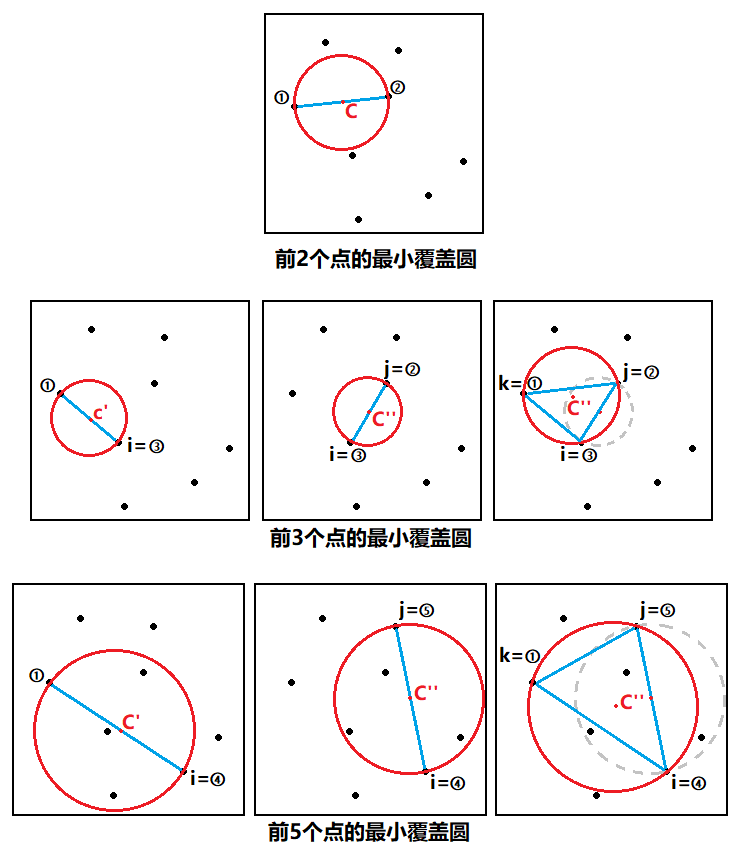
2)以第①個點和第②個點為直徑建立初始圓C,如圖三-3-2所示。然後依次判斷剩下n-2個點是否在這個圓內。
圖三-3-1
2)以第①個點和第②個點為直徑建立初始圓C,如圖三-3-2所示。然後依次判斷剩下n-2個點是否在這個圓內。
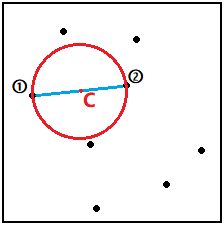 圖三-3-2
如果點p[i]在圓C內(3<=i<=n),則不做任何處理;否則p[i]必定在前i個點所在最小覆蓋圓的邊界上,求出這個圓後更新C。於是問題轉化成:求前i個點的最小覆蓋圓,並且點p[i]在圓上。
3)以第①個點和第i個點p[i]為直徑建立初始圓C'。然後依次判斷前i個點是否在這個圓內。
圖三-3-2
如果點p[i]在圓C內(3<=i<=n),則不做任何處理;否則p[i]必定在前i個點所在最小覆蓋圓的邊界上,求出這個圓後更新C。於是問題轉化成:求前i個點的最小覆蓋圓,並且點p[i]在圓上。
3)以第①個點和第i個點p[i]為直徑建立初始圓C'。然後依次判斷前i個點是否在這個圓內。
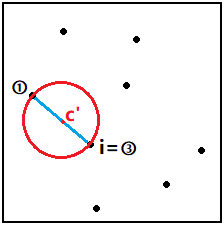 圖三-3-3
如果點p[j]在圓C'內(j < i),則不做任何處理;否則p[j]必定在前j個點所在最小覆蓋圓的邊界上,求出這個圓後更新C'。於是問題轉化成:求前j個點的最小覆蓋圓,並且點p[i]和點p[j]都在圓上。
4)以第i個點和第j個點為直徑建立初始圓C''。然後依次判斷前j個點是否在這個圓內。
圖三-3-3
如果點p[j]在圓C'內(j < i),則不做任何處理;否則p[j]必定在前j個點所在最小覆蓋圓的邊界上,求出這個圓後更新C'。於是問題轉化成:求前j個點的最小覆蓋圓,並且點p[i]和點p[j]都在圓上。
4)以第i個點和第j個點為直徑建立初始圓C''。然後依次判斷前j個點是否在這個圓內。
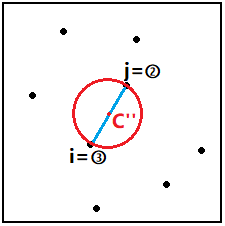 圖三-3-4
如果點p[k]在圓C''內(k < j),則不做任何處理;否則用點p[i]、p[j]、p[k]三點確定一個圓更新C'',繼續判斷剩下的點l (k < l < j)。
圖三-3-4
如果點p[k]在圓C''內(k < j),則不做任何處理;否則用點p[i]、p[j]、p[k]三點確定一個圓更新C'',繼續判斷剩下的點l (k < l < j)。
 圖三-3-5
5)然後用C''更新C',再用C'更新C。就這樣迭代求出包含前i個點的最小包圍圓C。最後來看一下前5個點的最小覆蓋圓。
圖三-3-5
5)然後用C''更新C',再用C'更新C。就這樣迭代求出包含前i個點的最小包圍圓C。最後來看一下前5個點的最小覆蓋圓。
 圖三-3-6
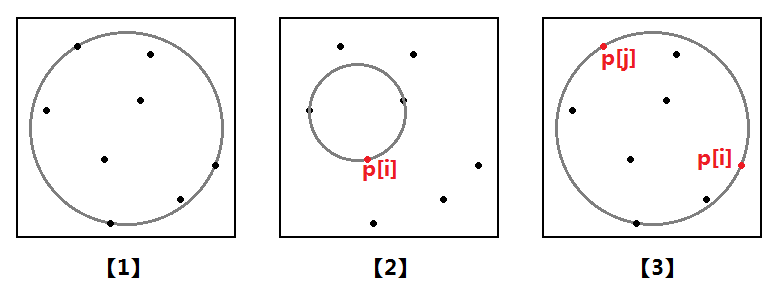
可能這樣講下來有點迷,那麼我們仔細分析一下上述演算法。首先該問題有幾個子問題,如圖三-3-7所示,分別為:
【1】前i個點的最小覆蓋圓;
【2】前i個點的最小覆蓋圓,且點p[i]在該圓邊界上;
【3】前j個點的最小覆蓋圓,且點p[i]和點p[j]在該圓邊界上;
圖三-3-6
可能這樣講下來有點迷,那麼我們仔細分析一下上述演算法。首先該問題有幾個子問題,如圖三-3-7所示,分別為:
【1】前i個點的最小覆蓋圓;
【2】前i個點的最小覆蓋圓,且點p[i]在該圓邊界上;
【3】前j個點的最小覆蓋圓,且點p[i]和點p[j]在該圓邊界上;
 圖三-3-7
圖三-3-7
這樣把狀態一劃分,問題就變得簡單許多了。自底向上的分析,【3】的情況我們已知圓上兩點,那麼只要再知道一個點就可以直接採用圓心(未知量)到圓邊界點(已知量)距離相等列方程求解二元一次方程組計算得到(即三點確定一個圓),所以列舉所有前j個點計算半徑最大的那個圓就是【3】問題的解。而【2】的情況是我們已知圓上一點,那麼再列舉一點就可以轉變成【3】的情況。同樣,【1】的情況是隻要列舉一點就可以轉變成【2】的情況,自底向上的遞迴求解即可。 最小覆蓋圓參考程式碼如下: 最小覆蓋圓 4、O(n)演算法時間複雜度分析 如果沒有一開始的洗牌演算法,考察該演算法將會有三個for迴圈,那麼最壞情況就是每次加入的點都在前i個點組成覆蓋圓的外面,所以演算法的最壞時間複雜度還是O(n^3)的。但是一旦順序打亂以後,情況就不同了。 有一條很重要的性質就是:第i個點在前i-1個點所組成的最小覆蓋圓外的概率為3/i。 證明如下:隨機生成i個點,求出它們的最小覆蓋圓,這個最小覆蓋圓必然是圓上的某3個點確定的(2個點的情況計算得到的概率更小所以不考慮)。那麼最後生成的那個點(第i個點)只要不是那3個點中其中一個,則必然落在圓內;反之在圓外。所以第i個點在前i-1個點組成的最小覆蓋圓外側的概率僅為3/i。 對於第i個點,只有3/i的概率是需要重新計算前i個點的最小覆蓋圓,其它情況都是pass,所以總的均攤複雜度是O(n)的。 四、最小包圍球 1、O(n)演算法 最後我們將上述問題擴充套件為三維(如果對最小覆蓋圓演算法還沒有完全理解請止步於此)。 演算法思路完全參照二維求最小覆蓋圓的情況: 1)隨機增量法,打亂所有點的順序。 2)【前i個點的最小包圍球】以第①個點和第②個點為直徑,兩點中點為球心,建立初始球C。然後依次判斷其它點是否在這個球體內,如果點p[i]在球C內(3<=i<=n),則不做任何處理;否則p[i]必定在前i個點所在最小包圍球的邊界上,求出這個球后更新C。於是問題轉化成:求前i個點的最小包圍球,並且點p[i]在球上。 3)【前i個點的最小包圍球,且經過點 p[i]】以第①個點和第i個點p[i]為直徑建立初始球C'。然後依次判斷前i個點是否在這個球內。如果點p[j]在球C'內(j < i),則不做任何處理;否則p[j]必定在前j個點所在最小包圍球的邊界上,求出這個球后更新C'。於是問題轉化成:求前j個點的最小包圍球,並且點p[i]和點p[j]都在球上。 4)【前j個點的最小包圍球,且經過點 p[i]和p[j]】以第①個點、第i個點p[i]、第j個點p[j]三點確定一個空間圓,以這個空間圓的圓心建立初始球C''。然後依次判斷前j個點是否在這個球內。如果點p[k]在球C''內(k < j),則不做任何處理;否則p[k]必定在前k個點所在最小包圍球的邊界上,求出這個球后更新C''。於是問題轉化成:求前k個點的最小包圍球,並且點p[i]、點p[j]、點p[k]都在球上。 5)【前k個點的最小包圍球,且經過點 p[i]、p[j]、p[k]】以點p[i]、點p[j]、點p[k]三點確定一個空間圓,以這個圓的圓心建立初始球C'''。然後依次判斷前k個點是否在這個球內。如果點p[l]在球C'''內(l < k),則不做任何處理;否則p[i]、p[j]、p[k]、p[l]四點確定一個球,求出所有這些球中半徑最大的更新C'''。最後用C'''更新C'',用C''更新C',再用C'更新C。得到前i個點的最小包圍球。 雖然演算法描述異常枯燥,但是2、3、4、5其實是類似的步驟,實際實現的時候還是很簡單的。 最小包圍圓參考程式碼如下: 最小包圍球 最後講一下第5步中三點確定球和四點確定球的計算方式。 2、空間三點外心 空間三點確定的最小包圍球的球心一定是三點外接圓圓心(如圖三-2-1中的O點,三角形ABC在球O的一個徑面上),首先O在平面ABC上,所以我們先要求出平面ABC的表示式。
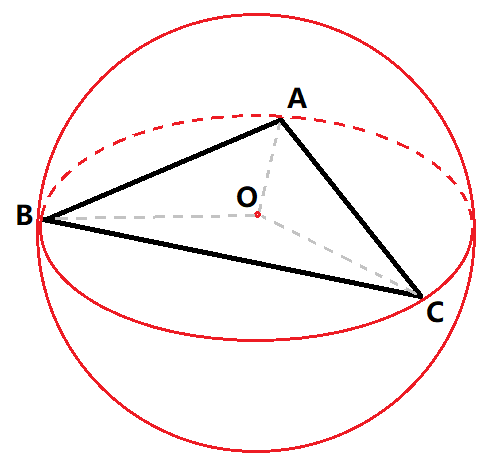 如圖三-2-1
如圖三-2-1
a) 點法式計算平面 平面方程用點法式表示為:
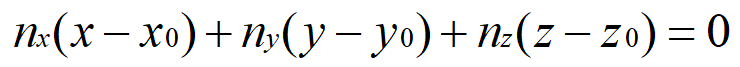 其中(nx,ny,nz)代表平面法向量,(x0,y0,z0)為平面上一點,那麼現在就是要求平面法向量n,我們利用三維向量的叉乘來實現。
其中(nx,ny,nz)代表平面法向量,(x0,y0,z0)為平面上一點,那麼現在就是要求平面法向量n,我們利用三維向量的叉乘來實現。
 如圖三-2-2
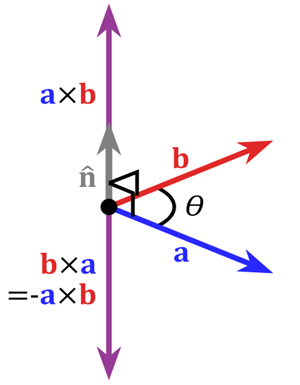
如圖三-2-2,右手法則,四個手指按逆時針方向握緊(從a握到b),大拇指指向方向表示向量a和向量b所在的平面的法向量方向,即a×b。則有:
如圖三-2-2
如圖三-2-2,右手法則,四個手指按逆時針方向握緊(從a握到b),大拇指指向方向表示向量a和向量b所在的平面的法向量方向,即a×b。則有:
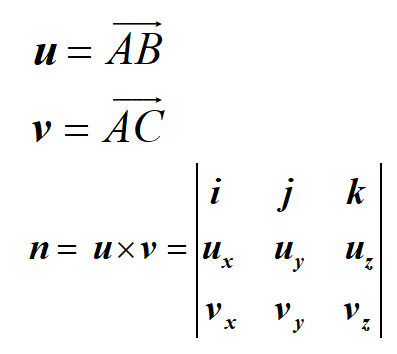 如圖三-2-3
利用對角線法則,可得:
如圖三-2-3
利用對角線法則,可得:
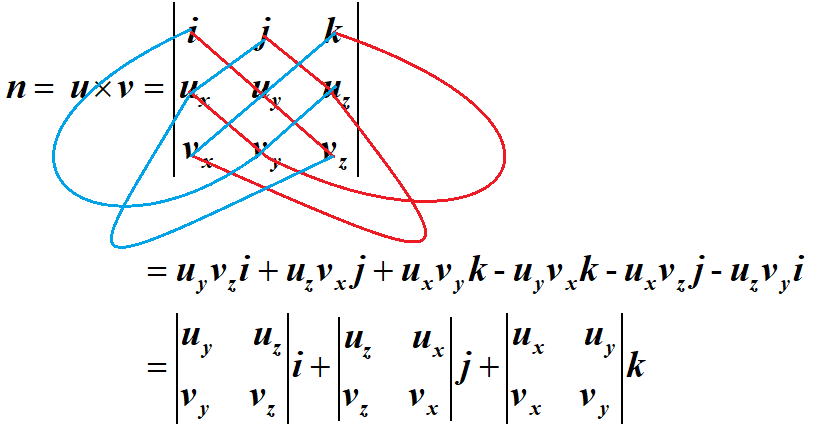
如圖三-2-4 最後用A點(或B、C點皆可)替代(x0, y0, z0),代入點法式方程,就計算得出了平面ABC的一般式(A、B、C、D為常數):
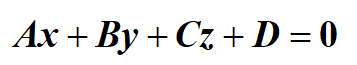
b) 距離法計算外心 令O為空間三角形ABC的外心,|OA|=|OB|=|OC|,拿|OA|=|OB|舉例,有:
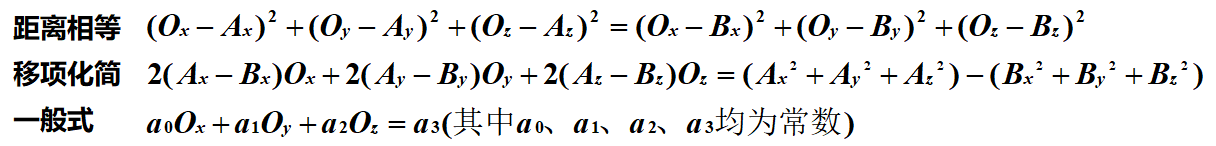
如圖三-2-5 然後聯合|OB|=|OC|以及點O在平面ABC上得到三個方程三個未知數,利用高斯消元求解(Ox,Oy,Oz)(以前寫的一個高斯消元的演算法簡介: 高斯消元 )。
 如圖三-2-6
3、空間四點球心
首先,我們要排除任意三點共線和四點共面的情況,對於最小包圍球求解過程中不會出現這樣的情況(請讀者自行思考)。所以我們只需要考慮四點不共面的情況。不共面的四點必然能夠確定一個球,假設球心為O,則必然滿足O到球面上的四點A、B、C、D距離相等。
如圖三-2-6
3、空間四點球心
首先,我們要排除任意三點共線和四點共面的情況,對於最小包圍球求解過程中不會出現這樣的情況(請讀者自行思考)。所以我們只需要考慮四點不共面的情況。不共面的四點必然能夠確定一個球,假設球心為O,則必然滿足O到球面上的四點A、B、C、D距離相等。
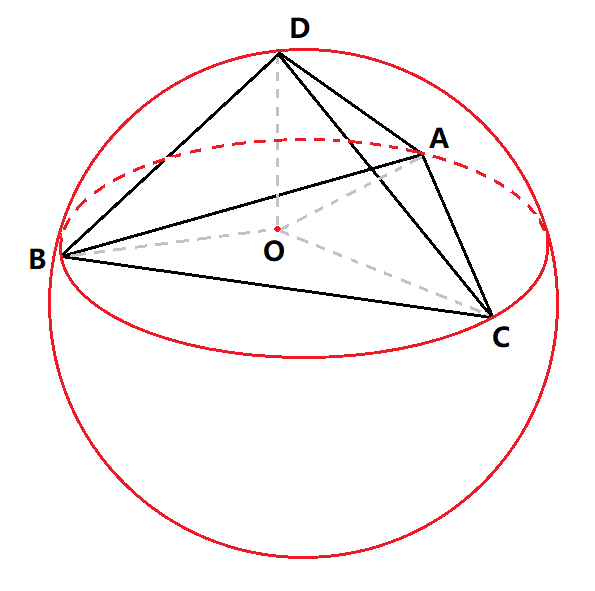 如圖三-3-1
還是利用距離的兩兩相等,得到三個三元一次的方程,同樣利用高斯消元求解(Ox,Oy,Oz)即可:
如圖三-3-1
還是利用距離的兩兩相等,得到三個三元一次的方程,同樣利用高斯消元求解(Ox,Oy,Oz)即可:
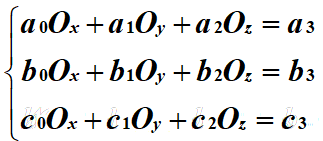 如圖三-3-2
五、最小包圍球相關題集整理
如圖三-3-2
五、最小包圍球相關題集整理
最小覆蓋圓 ZJU 1450 Minimal Circle HDU 3007 Buried memory HDU 3932 Groundhog Build Home BZOJ 2823 訊號塔
最小包圍球 PKU 2069 Super Star HDU 2226 Stars
