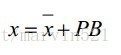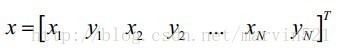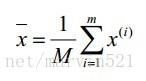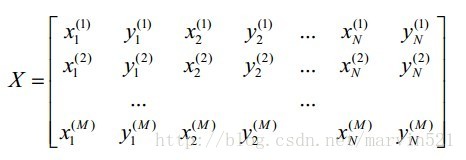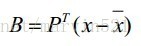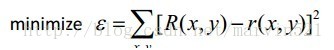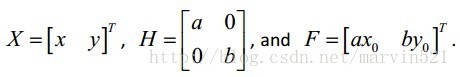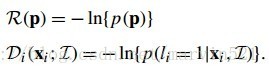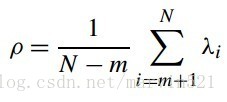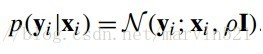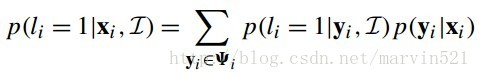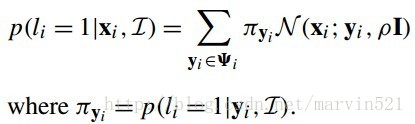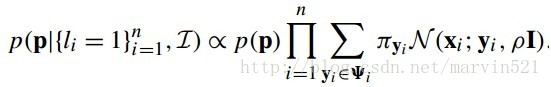人臉識別之人臉對齊(四)--CLM演算法及概率圖模型改進
原文:
http://blog.csdn.net/marvin521/article/details/11489453
04、概率圖模型應用例項
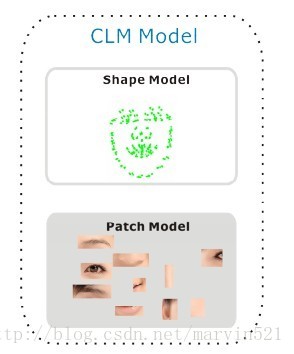
最近一篇文章《Deformable Model Fitting by Regularized Landmark Mean-Shift》中的人臉點檢測演算法在速度和精度折中上達到了一個相對不錯的水平,這篇技術報告就來闡述下這個演算法的工作原理以及相關的鋪墊演算法。再說這篇文章之前,先說下傳統的基於CLM(Constrained local model)人臉點檢測演算法的不足之處,ASM也屬於CLM的一種,CLM顧名思義就是有約束的區域性模型,它通過初始化平均臉的位置,然後讓每個平均臉上的特徵點在其鄰域位置上進行搜尋匹配來完成人臉點檢測。整個過程分兩個階段:模型構建階段和點擬合階段。模型構建階段又可以細分兩個不同模型的構建:形狀模型構建和Patch模型構建,如(圖一)所示。形狀模型構建就是對人臉模型形狀進行建模,說白了就是一個ASM的點分佈函式(PDM),它描述了形狀變化遵循的準則。而Patch模型則是對每個特徵點周圍鄰域進行建模,也就說建立一個特徵點匹配準則,怎麼判斷特徵點是最佳匹配。
(圖一) CLM模型:形狀模型和Patch模型
下面就來詳細說下CLM演算法流程:
一、模型構建之形狀模型構建(延續ASM的形狀模型函式),如(公式一)所示:
(公式一)
(公式一)中X-bar表示平均臉,P是形狀變化的主成分組成的矩陣,它是一個關鍵的引數,下面就來看看它是如何得到的。假設我們有M張圖片,每張圖片有N個特徵點, 每個特徵點的座標假設為(xi,yi),一張影象上的N個特徵點的座標組成的向量用
(公式二)
然後每張臉組成的向量都減去這個平均臉向量,就得到一個均值為0的形狀變化矩陣X,如下表示:
一定要注意X此時是一個零均值的形狀變化矩陣,因為每個行向量都減去了平均臉向量,也就是相對於平均臉的偏差,對XX’進行主成分分析,得到形狀變化的決定性成分,即特徵向量Pj以及相對應的特徵值λj,選擇前K個特徵向量以列排放的方式組成形狀變化矩陣P,這些特徵向量其實就是所有樣本變換的基,可以表述樣本中的任意變化。有了形狀變化矩陣P,(公式一)中的B就可以通過(公式三)得出:
(公式三)
(公式三)中求出的B其實是形狀變化的權重向量,決定哪些特徵點起著關鍵作用。到這裡就完成模型構建,當給定一個權重B時,我們就可以用(公式一)重建出一個形狀,這個權重B在以後點擬合階段起著關鍵作用。
二、模型構建之Patch模型構建
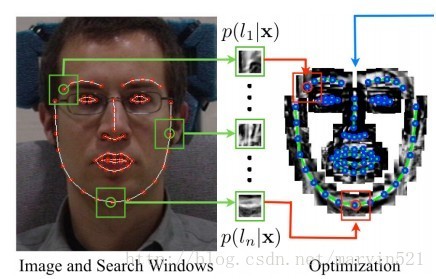
在構建好形狀模型之後,我們就可以在檢測到的人臉上初始化一個人臉形狀模型,接下來的工作就是讓每個點在其鄰域範圍內尋找最佳匹配點。傳統的ASM模型就是沿著邊緣的方向進行塊匹配,點匹配等各種低階匹配,匹配高錯誤率導致ASM的效能不是很好。後續各種改進版本也就出來了,大部分做法都是對候選匹配特徵點鄰域內的塊進行建模,我們統稱他們為有約束的區域性模型:CLM。這裡先以基於SVM的匹配作為例子來說,因為這些都是鋪墊知識,引出改進的演算法。當我們初始化每個特徵點後,用訓練好的SVM對每個特徵點周圍進行打分,就像濾波器一樣,得到一個打分響應圖(response map),標識為R(X,Y),如(圖二)所示:
(圖二) 特徵點(左)其鄰域響應圖(右)
接下來就是對響應圖擬合一個二次函式,假設R(X,Y)是在鄰域範圍內(x0,y0)處得到最大值,我們對這個位置擬合一個函式,使得位置和最大值R(X,Y)一一對應。擬合函式如(公式四)所示:
(公式四) 擬合最大響應位置二次函式
(公式四)中的a,b,c是我們要求的擬合二次函式的引數,求解方法就是使擬合函式r(x,y)和R(X,Y)之間的誤差最小,即完成一個最小二乘法計算,如(公式五)所示:
(公式五) 求取(公式四)的最小二乘法
通過(公式五)完成最小二乘法運算後得到(公式四)的引數a,b,c,有了引數a,b,c,那麼r(x,y)其實就是一個關於特徵點位置的目標代價函式,然後再加上一個形變約束代價函式就構成了特徵點查詢的目標函式,每次優化這個目標函式得到一個新的特徵點位置,然後在迭代更新,直到收斂到最大值,就完成了人臉點擬合。目標函式如(公式六)所示:
(公式六) 目標函式
在(公式六)的目標函式中第二項就是形狀約束,b是上面說的形變成分的權重,而lambda則是形變成分(主成分分析中的空間軸)對應的幅度(主成分分析的特徵值)。對於整個目標函式,你可以這樣理解,第一項是擬合位置作為新特徵點位置的代價,而這個位置的代價再減去平均形狀的變化,這樣就形成了位置和形狀兩種約束的制約,如果一個在一個歧義的位置得到的r(x,y)分很高,但是離平均臉很遠,那麼f(x)值也會很小,那就不是最優值。我們比較關心的是目標函式中的兩項約束是否是一一對應,等比例增長的。這點不用擔心,如果把(公式六)展開用矩陣的形式寫出來的話,可以變成(公式七)的樣子:
(公式七) 目標函式展開
其中
可以看出(公式七)是個關於特徵點位置X的二次凸函式,有全域性最優解。每次求出最優解,然後再計算鄰域響應圖,在求解直到收斂時就完成了特徵點的擬合查詢工作。
這個演算法理論還是可以,但有幾點不足:第一、從SVM裡得到的響應圖是否真實可靠?這點其實也正是要改進的地方。第二、每次迭代都要優化一個二次函式計算量也蠻大,這會拖慢速度,無法實時。第三、形變約束是否有爭議,能否讓你信服?而且形狀模型根本沒考慮到現實情況中的縮放,旋轉和平移。
帶著這三個問題,我們進入文章一開頭就提到的那篇文章的演算法,我們簡稱它為DMF_ MeanShift, DMF_MeanShift使用的點分佈模型(形狀模型)如(公式八)所示:
(公式八)點分佈模型
(公式八)中的要求引數為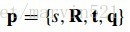
(公式九)
這裡要注意一下,R(P)表示形變約束,對應CLM(公式六)中的第二項,D表示匹配代價,對應CLM(公式六)中的第一項。這兩項在DMF_MeanShift中都要發生變化,不再使用CLM中的約束規則,而使用概率分佈的形式來表述,全部在概率圖模型的框架中完成推理求解,下面來看看是如何把(公式九)中的兩項約束轉換成概率約束的。
對於(公式九)中的求取形狀模型引數的目標函式,在概率模型中可以描述成一個當所有特徵點都匹配最優時模型引數的最大似然。意思就是說在訓練樣本中,給定所有樣本點匹配最優時的最大似然估計。當給定影象塊時,每個檢測器之間是相互獨立的(這個條件獨立有爭議,我現在還沒有徹底推倒出來),那麼這個似然函式可以寫成(公式十)的形式:
(公式十)
在(公式十)中,左邊表示給定匹配點和影象塊時,引數的似然函式,右邊則是條件獨立分解。其中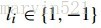
(公式十一)
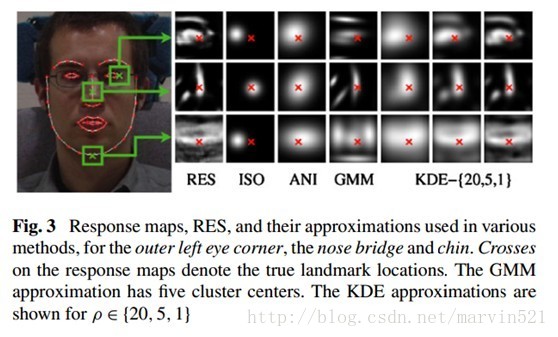
(公式十一)中的兩項就和CLM中的兩項約束對應上了,而且轉換到了概率空間,接下來的步驟就是對這兩項的分佈進行近似估計。估計的方法很多,而且很複雜,這裡為了方便理解,先貼出幾個估計方法的對比效果圖,如(圖三)所示:
(圖三)
在(圖三)中RES表示真實響應圖,而ISO,ANI,GMM和KDE分別表示各向同性高斯估計、各向異性高斯估計、混合高斯估計和核密度估計,從(圖三)中可以看出基於核密度估計得逼近分佈和真實響應圖最接近。由於前三個近似逼近方法效果不好,而且推導過程複雜,這裡就不再說了,只簡單說下效果最好的KDE逼近方法。
由於在(公式一)中的形變矩陣P扔掉了一些很小的成分,因此重建的形狀點並不是百分百正確,有一定的誤差,我們可以這個誤差看成觀察噪聲,它服從同方差各向同性高斯分佈,如(公式十二)所示:
(公式十二)
其中ρ表示噪聲的協方差,可以通過(公式十三)求出(Moghaddam and Pentland1997):
(公式十三)
其實就是主成分分析中特徵值的算術平均,通過(公式十二)我們也可以得到給定Xi時yi的條件概率,如(公式十四)所示:
(公式十四)
(公式十四)的推倒是通過混合高斯分佈推倒出來的,這裡也不再推倒。假設特徵點候選區域為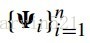
(公式十五)
綜合(公式十四)和(公式十五),我們得到一個非參形式的響應圖近似估計,如(公式十六)所示:
(公式十六)
把(公式十六)這個匹配代價約束帶入(公式十)中,我們得到最一個關於引數P的似然概率分佈函式,如(公式十七)所示:
(公式十七)
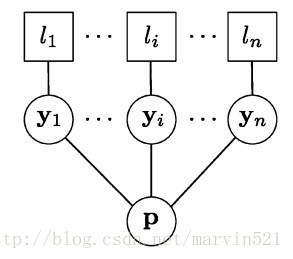
只要求解此最大似然函式就可以求出引數P,也就是求取使得關於引數P的邊緣概率最大時對應的引數P,這是一個無向圖模型,如果你不能抽象出圖模型,可以參看(圖四)所示:
(圖四)
(圖四)中Li表示觀察,y表示隱藏變數,P表示引數。這個關於P的邊緣概率可以通過概率圖模型的中的BP演算法求解,有興趣的可以翻看參考文獻[6]的Appendix。這裡採用另外一種求解方法:EM演算法。因為真實位置標籤y我們不知道,是個隱變數,而且引數P也不知道,很自然的就想到了EM演算法。EM演算法的推倒也比較複雜,這裡就直接貼圖了,反正最後的結論才是我們想要的,如(圖五)所示。
(圖五)
(圖五)中的等式(33)對應本文的(公式十七)。最後得到的等式(36)就是我們想要的梯度,有了梯度就可以更新引數P,而且也可以通過(公式十八)來更新候選特徵點匹配的位置:
(公式十八)
(公式十八)的得出是在參考文獻[6]的各向同性高斯逼近方法中推倒出來的,用的是泰勒展開方法,這裡的推倒在後續有時間再補充。這樣通過更新特徵點匹配位置,有了新位置然後計算deltaP,然後更新引數P,重複上述過程直到引數P收斂為止,就完成了特徵點匹配檢測。整個過程有點像Mean-Shift演算法,所以演算法名中出現Mean-Shift。這個演算法的好處就是融合進了各種形變引數,並且使得引數可以迭代更新,更新速度也挺快。
本篇文章只能算是介紹下概率圖圖模型的一個應用,瞭解人臉特徵點檢測詳細原理需要閱讀參考文獻[6],歡迎提供關於各向同性高斯估計、各向異性高斯估計、混合高斯估計和核密度估計的相關資料和討論。
參考文獻:
[1] Gaussian mean-shift is an EM algo-rithm.Carreira-Perpinan, M. (2007)
[2] On the number of modes of a Gaussianmixture. Carreira-Perpinan, M., & Williams, C. (2003)
[3] Active shape models—‘smart snakes’.Cootes, T., & Taylor, C. (1992)
[4] Constrained Local Model for FaceAlignment. Xiaoguang Yan(2011)
[5] Face Alignment through SubspaceConstrained Mean-Shifts. Jason M. Saragih(2009)
[6] Deformable Model Fitting by RegularizedLandmark Mean-Shift. Jason M. Saragih(2011)
[7] Support vector tracking. Avidan, S.(2004)