人臉識別之人臉對齊(六)--ERT演算法
1.概述
文章名稱:One Millisecond Face Alignment with an Ensemble of Regression Trees
文章來源:2014CVPR
文章作者:Vahid Kazemi ,Josephine Sullivan
簡要介紹:One Millisecond Face Alignment with an Ensemble of Regression Trees演算法(以下簡稱GBDT)是一種基於迴歸樹的人臉對齊演算法,這種方法通過建立一個級聯的殘差迴歸樹(GBDT)來使人臉形狀從當前形狀一步一步迴歸到真實形狀。每一個GBDT的每一個葉子節點上都儲存著一個殘差迴歸量,當輸入落到一個節點上時,就將殘差加到改輸入上,起到迴歸的目的,最終將所有殘差疊加在一起,就完成了人臉對齊的目的。
在逐步詳細介紹GBDT之前,按照慣例,先介紹人臉對齊的基本概念和原理。
2.人臉對齊(Face Alignment)基本概念及原理
人臉對齊中的幾個關鍵詞:
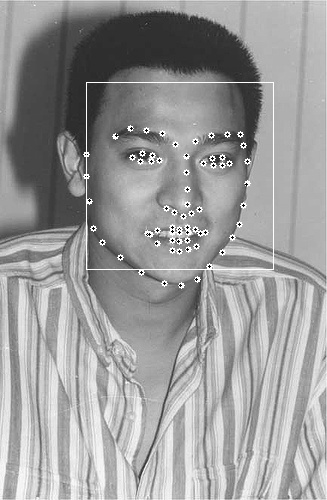
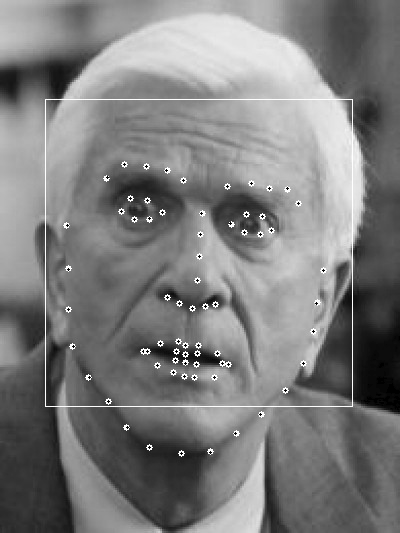
形狀(shape):形狀就是人臉上的有特徵的位置,如下圖所示,每張圖中所有黃點構成的圖形就是該人臉的形狀。
特徵點(landmark):形狀由特徵點組成,圖中的每一個黃點就是一個特徵點。

人臉對齊的最終目的就是在已知的人臉方框(一般由人臉檢測確定人臉的位置)上定位其準確地形狀。
人臉對齊的演算法主要分為兩大類:基於優化的方法(Optimization-based method)和基於迴歸的方法(Regression-based method)。
本文的方法屬於基於迴歸的方法。
3.從“樹”的概念開始
樹的思想在機器學習演算法中可謂是鼎鼎大名,非常常用的決策樹、二叉樹等,以及由樹構成的隨機森林等演算法,都在各種領域被廣泛使用,甚至延伸出了諸如“隨機蕨”等類樹的結構。樹不僅多種多樣,其應用也絕不僅僅侷限於分類,例如本文就將樹的思想應用在迴歸的領域,而非常流行的CART分類迴歸樹也是其中一種,甚至還有采用樹的結構來提取特徵的方法(3000FPS)。
如果大家理解隨機森林,那麼對本文的GBDT可能會更好理解一點。簡單來說隨機森林就是將很多棵決策樹聯合在一起,其中每一棵樹的訓練採用的是隨機數量的樣本和隨機的特徵,其實也是整合學習的思想的表現之一。
而本文的GBDT,相比與隨機森林,其實本質上差別不是很大,主要差別在於:
1)每一棵樹之間的關係是序列的,並非是並行的關係,也就是說後一棵樹的建立在前一棵樹的基礎之上。
2)每一棵樹的葉子節點上存的是殘差,這也是GBDT的特點之一,也只有通過葉子節點上儲存的殘差,才能使形狀不斷地迴歸,從而回歸到真實形狀。
下面直接介紹這種方法。
4.人臉對齊中的一棵GBDT
假設我要開始構建一棵GBDT,注意,這裡的一棵GBDT的概念不是指一棵樹,而是指很多棵樹,很多棵樹構成一個GBDT,所以說GBDT的地位類似與隨機森林,都是由樹整合構成的。
構建一棵GBDT要實現的目的是:通過這棵樹,將人臉的初始形狀迴歸到其真實形狀上去(這是測試時的目的,訓練時,也就是構建樹時我們是知道其真實形狀的,那麼目的自然就是用GBDT來表示初始形狀和真實形狀的關係)。
假設我們一共有N幅影象,將它們作為訓練樣本,我們知道這N幅影象的每一個真實形狀。首先我們要獲得一個迴歸的初始形狀,假設我們用所有影象的平均形狀來作為這個初始形狀(初始形狀就是迴歸的起點,之後在測試時無論給出怎樣一幅影象,我們都通過這個初始形狀來進行預測和迴歸)。在原論文中,在訓練時,作者並非只使用了初始形狀,而是隨機挑選另一個真實形狀來作為某一幅影象的初始形狀,這種做法我們先不討論,首先討論如何構建一棵GBDT。
現在開始構建GBDT的第一棵樹。
有了初始形狀,這裡就會發現一個問題,假如使用平均形狀來作為每一幅影象的初始形狀,那麼對所有影象來說,初始輸入都是相同的,這如何分裂樹呢?是的,對所有影象來說,初始形狀相同,但我們分裂樹時,採用的輸入並非是當前形狀,而是依據當前形狀從該圖片中提取出的特徵。對於每一幅影象來說,初始形狀雖然相同,但每一幅圖片都不同,因此提取出的特徵也就不同,論文中是使用的畫素差作為特徵,下一節會詳細講這種特徵的提取方式。我們依據特徵來進行節點的分裂操作,直至到達樹的葉子節點。
當我們把N張圖片都輸入這第一棵樹,自然每一張圖片最終都會落入其中的一個葉子節點,比如第1張圖片落入了第3個葉子節點,第2張圖片落入了第1個葉子節點,第3張圖片落入了第三個葉子節點等等。這樣,每一個葉子節點中都會有圖片落入,當然也可能沒有,這無所謂。這時,我們就要計算殘差,計算每一個圖片的當前形狀和真實形狀的差值,之後,在同一個葉子節點中的所有圖片的差值作平均,就是該葉子節點應當儲存的殘差。當所有葉子節點都儲存了殘差後,第一棵樹也就構造完畢了。
在構造第二棵樹之前,我們要把每張圖片的當前形狀做一個更新,也就是要將當前形狀更新成:當前形狀+殘差。對應到第一棵樹,即是初始形狀加上殘差,這樣每一張圖片的當前形狀就從初始形狀變成了初始形狀加殘差,距離真實形狀又更近了一步。
之後再用同樣的方法構建第二棵樹,依據特徵進行節點分裂,直到葉子節點。在葉子節點中計算每一張圖片當前形狀和真實形狀的差,然後取平均,將這個平均值儲存在該葉子節點中,作為殘差。之後更新每一張圖片的當前形狀,即將葉子節點中儲存的殘差加上其當前形狀,作為新的當前形狀,然後就可以建立第三棵樹了。
直至建立的樹足夠多,可以最後的當前形狀表示真實形狀,那麼這一個GBDT也就建立完成了。
還有一個問題沒有解決,那就是GBDT中的每一棵樹是怎樣分裂的,下面詳細敘述分裂的方法。
5.樹的接點分裂和畫素差特徵
對於一棵GBDT(很多棵子樹構成)而言,我們要建立一個特徵池,這個特徵池裡是我們隨機挑選的一些點的座標,然後對於每一幅影象,這些點都對應著不同的畫素值,因此,在樹的節點分裂時,我們首先會在這合格特徵池中隨機挑選兩個點,然後計算每一張圖片在這兩個點處的畫素值,然後計算每一張圖片的這兩個點處的畫素值的畫素差,之後隨機產生一個分裂閾值,根據這個閾值進行判斷,如果一幅影象的畫素差小於這個閾值,就往左分裂,否則往右分裂,將所有圖片都這樣判斷一次,就將所有圖片分成了兩部分,一部分在左,一部分在右。我們重複上面這個過程若干次,看看哪一次分裂的好(判斷是否分裂的好的依據是方差,如果分在左邊的樣本的方差小,這說明它們是一類,分的就好),就把這個分裂的好的選擇儲存下來,即儲存下這兩個點的座標值和分裂閾值。這樣一個節點的分裂就完成了。然後每一個節點的分裂都按照這個步驟進行,直到分裂到葉子節點。
6.作者的實驗結果
原論文作者一共建立了10棵GBDT,每一個GBDT中包含500棵樹,10棵GBDT的意思就是,每一棵GBDT都是相互獨立的,一共有10個相互獨立的特徵池。作者的每一個特徵池中有400個點,在同一棵GBDT中,每次節點分裂,都從這400個點中挑選出20對點並隨機產生20個閾值,然後進行分裂,看看哪一對點分裂的結果方差最小,就將其作為分裂的依據。
下面幾個圖是實驗結果