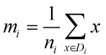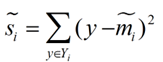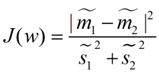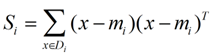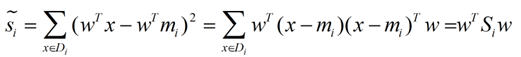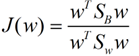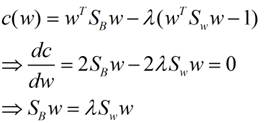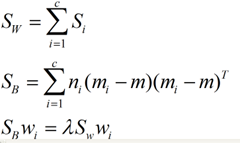背景：為什麼需要特徵抽取？

    基於的向量空間模型有個缺點，即向量空間中的每個關鍵詞唯一地代表一個概念或語義單詞，也就是說它不能處理同義詞和多義詞，然而實際情況是：一個詞往往有多個不同的含義，多個不同的詞可以代表一個概念。在這種情況下，基於的向量空間模型不能很好的解決這種問題。  

  特徵抽取方法則可以看作從測量空間到特徵空間的一種對映或變換,一般是通過構造一個特徵評分函式,把測量空間的資料投影到特徵空間,得到在特徵空間的值,然後根據特徵空間中的值抽取最高的若干個特徵。

    常用的特徵抽取方法主要有線性判別分析（LDA）、主成分分析（PCA）、潛在語義索引（LSI）、非負矩陣分解，因子分析，單詞聚類，規則提取

1、LDA（線性判別分析） 既可以用於降維，也可以用於多文字的多分類。

LDA是有監督的方式，它先對訓練資料進行降維，然後找出一個線性判別函式。

LDA的全稱是Linear Discriminant Analysis（線性判別分析），是一種supervised learning。有些資料上也稱為是Fisher’s Linear Discriminant，因為它被Ronald Fisher發明自1936年，Discriminant這次詞我個人的理解是，一個模型，不需要去通過概率的方法來訓練、預測資料，比如說各種貝葉斯方法，就需要獲取資料的先驗、後驗概率等等。LDA是在目前機器學習、資料探勘領域經典且熱門的一個演算法，據我所知，百度的商務搜尋部裡面就用了不少這方面的演算法。

    LDA的原理是，將帶上標籤的資料（點），通過投影的方法，投影到維度更低的空間中，使得投影后的點，會形成按類別區分，一簇一簇的情況，相同類別的點，將會在投影后的空間中更接近。要說明白LDA，首先得弄明白線性分類器：因為LDA是一種線性分類器。對於K-分類的一個分類問題，會有K個線性函式：

     當滿足條件：對於所有的j，都有Yk > Yj,的時候，我們就說x屬於類別k。對於每一個分類，都有一個公式去算一個分值，在所有的公式得到的分值中，找一個最大的，就是所屬的分類了。

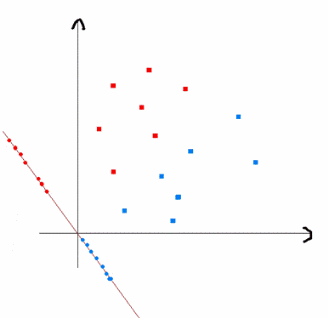
    上式實際上就是一種投影，是將一個高維的點投影到一條高維的直線上，LDA最求的目標是，給出一個標註了類別的資料集，投影到了一條直線之後，能夠使得點儘量的按類別區分開，當k=2即二分類問題的時候，如下圖所示：

     紅色的方形的點為0類的原始點、藍色的方形點為1類的原始點，經過原點的那條線就是投影的直線，從圖上可以清楚的看到，紅色的點和藍色的點被原點明顯的分開了，這個資料只是隨便畫的，如果在高維的情況下，看起來會更好一點。下面我來推導一下二分類LDA問題的公式：

     假設用來區分二分類的直線（投影函式)為：

    LDA分類的一個目標是使得不同類別之間的距離越遠越好，同一類別之中的距離越近越好，所以我們需要定義幾個關鍵的值。

    類別i的原始中心點為：（Di表示屬於類別i的點)

    類別i投影后的中心點為：

    衡量類別i投影后，類別點之間的分散程度（方差）為：

    最終我們可以得到一個下面的公式，表示LDA投影到w後的損失函式：

   我們分類的目標是，使得類別內的點距離越近越好（集中），類別間的點越遠越好。分母表示每一個類別內的方差之和，方差越大表示一個類別內的點越分散，分子為兩個類別各自的中心點的距離的平方，我們最大化J(w)就可以求出最優的w了。想要求出最優的w，可以使用拉格朗日乘子法，但是現在我們得到的J(w)裡面，w是不能被單獨提出來的，我們就得想辦法將w單獨提出來。

   我們定義一個投影前的各類別分散程度的矩陣，這個矩陣看起來有一點麻煩，其實意思是，如果某一個分類的輸入點集Di裡面的點距離這個分類的中心店mi越近，則Si裡面元素的值就越小，如果分類的點都緊緊地圍繞著mi，則Si裡面的元素值越更接近0.

   帶入Si，將J(w)分母化為：

   同樣的將J(w)分子化為：

   這樣損失函式可以化成下面的形式：

   這樣就可以用最喜歡的拉格朗日乘子法了，但是還有一個問題，如果分子、分母是都可以取任意值的，那就會使得有無窮解，我們將分母限制為長度為1（這是用拉格朗日乘子法一個很重要的技巧，在下面將說的PCA裡面也會用到，如果忘記了，請複習一下高數），並作為拉格朗日乘子法的限制條件，帶入得到：

   這樣的式子就是一個求特徵值的問題了。

   對於N(N>2)分類的問題，我就直接寫出下面的結論了：

   這同樣是一個求特徵值的問題，我們求出的第i大的特徵向量，就是對應的Wi了。

   這裡想多談談特徵值，特徵值在純數學、量子力學、固體力學、計算機等等領域都有廣泛的應用，特徵值表示的是矩陣的性質，當我們取到矩陣的前N個最大的特徵值的時候，我們可以說提取到的矩陣主要的成分。在機器學習領域，不少的地方都要用到特徵值的計算，比如說影象識別、pagerank、LDA、PCA等等。

下面我們利用LDA進行一個分類的問題：假設一個產品有兩個引數來衡量它是否合格，

我們假設兩個引數分別為：

所以我們可以根據上圖表格把樣本分為兩類，一類是合格的，一類是不合格的，所以我們可以建立兩個資料集類：

cls1_data =

    2.9500    6.6300

    2.5300    7.7900

    3.5700    5.6500

3.1600    5.4700

cls2_data =

    2.5800    4.4600

    2.1600    6.2200

    3.2700    3.5200

其中cls1_data為合格樣本，cls2_data為不合格的樣本，我們根據公式（1），（2）可以算出合格的樣本的期望值，不合格類樣本的合格的值，以及總樣本期望：

E_cls1 =

3.0525    6.3850

E_cls2 =

2.6700    4.7333

E_all =

2.8886    5.6771

我們可以做出現在各個樣本點的位置：

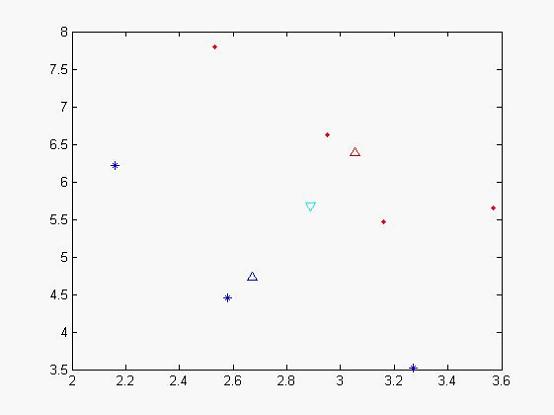
圖一

其中藍色‘*’的點代表不合格的樣本，而紅色實點代表合格的樣本，天藍色的倒三角是代表總期望，藍色三角形代表不合格樣本的期望，紅色三角形代表合格樣本的期望。從x，y軸的座標方向上可以看出，合格和不合格樣本區分度不佳。

我們在可以根據表示式（3），（4）可以計算出類間離散度矩陣和類內離散度矩陣：

Sb =

    0.0358    0.1547

0.1547    0.6681

Sw =

    0.5909   -1.3338

   -1.3338    3.5596

我們可以根據公式（7），（8）算出特徵值以及對應的特徵向量：

L =

    0.0000         0

         0    2.8837

對角線上為特徵值，第一個特徵值太小被計算機約為0了

與他對應的特徵向量為

V =

   -0.9742   -0.9230

0.2256   -0.3848

根據取最大特徵值對應的特徵向量：（-0.9230,-0.3848)，該向量即為我們要求的子空間，我們可以把原來樣本投影到該向量後 所得到新的空間（2維投影到1維，應該為一個數字）

new_cls1_data =

   -5.2741

   -5.3328

   -5.4693

   -5.0216

為合格樣本投影后的樣本值

new_cls2_data =

   -4.0976

   -4.3872

   -4.3727

為不合格樣本投影后的樣本值，我們發現投影后，分類效果比較明顯，類和類之間聚合度很高，我們再次作圖以便更直觀看分類效果

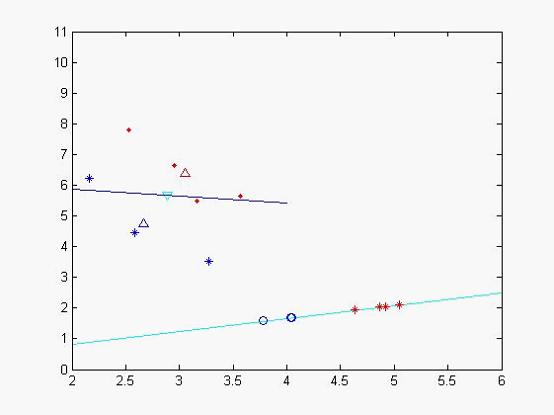
圖二

藍色的線為特徵值較小所對應的特徵向量，天藍色的為特徵值較大的特徵向量，其中藍色的圈點為不合格樣本在該特徵向量投影下來的位置，二紅色的‘*’符號的合格樣本投影后的資料集，從中個可以看出分類效果比較好（當然由於x，y軸單位的問題投影不那麼直觀）。

我們再利用所得到的特徵向量，來對其他樣本進行判斷看看它所屬的型別，我們取樣本點

（2.81，5.46），

我們把它投影到特徵向量後得到：result = -4.6947 所以它應該屬於不合格樣本。