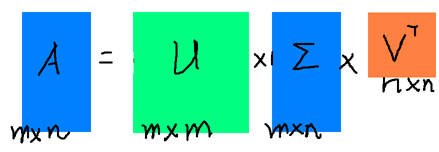http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html

一、奇異值與特徵值基礎知識：

    特徵值分解和奇異值分解在機器學習領域都是屬於滿地可見的方法。兩者有著很緊密的關係，我在接下來會談到，特徵值分解和奇異值分解的目的都是一樣，就是提取出一個矩陣最重要的特徵。先談談特徵值分解吧：

   1）特徵值：

    如果說一個向量v是方陣A的特徵向量，將一定可以表示成下面的形式：

    這時候λ就被稱為特徵向量v對應的特徵值，一個矩陣的一組特徵向量是一組正交向量。特徵值分解是將一個矩陣分解成下面的形式：

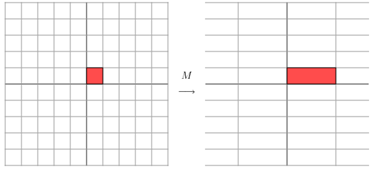
    其中Q是這個矩陣A的特徵向量組成的矩陣，Σ是一個對角陣，每一個對角線上的元素就是一個特徵值。我這裡引用了一些參考文獻中的內容來說明一下。首先，要明確的是，一個矩陣其實就是一個線性變換，因為一個矩陣乘以一個向量後得到的向量，其實就相當於將這個向量進行了線性變換。比如說下面的一個矩陣：

       它其實對應的線性變換是下面的形式：

    因為這個矩陣M乘以一個向量(x,y)的結果是：

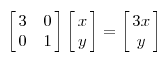    上面的矩陣是對稱的，所以這個變換是一個對x，y軸的方向一個拉伸變換（每一個對角線上的元素將會對一個維度進行拉伸變換，當值>1時，是拉長，當值<1時時縮短），當矩陣不是對稱的時候，假如說矩陣是下面的樣子：

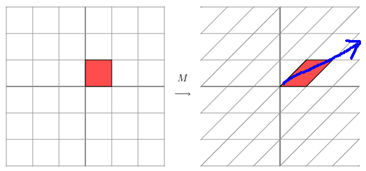
    它所描述的變換是下面的樣子：

    這其實是在平面上對一個軸進行的拉伸變換（如藍色的箭頭所示），在圖中，藍色的箭頭是一個最主要的變化方向（變化方向可能有不止一個），如果我們想要描述好一個變換，那我們就描述好這個變換主要的變化方向就好了。反過頭來看看之前特徵值分解的式子，分解得到的Σ矩陣是一個對角陣，裡面的特徵值是由大到小排列的，這些特徵值所對應的特徵向量就是描述這個矩陣變化方向（從主要的變化到次要的變化排列）

    當矩陣是高維的情況下，那麼這個矩陣就是高維空間下的一個線性變換，這個線性變化可能沒法通過圖片來表示，但是可以想象，這個變換也同樣有很多的變換方向，我們通過特徵值分解得到的前N個特徵向量，那麼就對應了這個矩陣最主要的N個變化方向。我們利用這前N個變化方向，就可以近似這個矩陣（變換）。也就是之前說的：提取這個矩陣最重要的特徵。總結一下，特徵值分解可以得到特徵值與特徵向量，特徵值表示的是這個特徵到底有多重要，而特徵向量表示這個特徵是什麼，可以將每一個特徵向量理解為一個線性的子空間，我們可以利用這些線性的子空間幹很多的事情。不過，特徵值分解也有很多的侷限，比如說變換的矩陣必須是方陣。

   （說了這麼多特徵值變換，不知道有沒有說清楚，請各位多提提意見。）

   2）奇異值：

    下面談談奇異值分解。特徵值分解是一個提取矩陣特徵很不錯的方法，但是它只是對方陣而言的，在現實的世界中，我們看到的大部分矩陣都不是方陣，比如說有N個學生，每個學生有M科成績，這樣形成的一個N * M的矩陣就不可能是方陣，我們怎樣才能描述這樣普通的矩陣呢的重要特徵呢？奇異值分解可以用來幹這個事情，奇異值分解是一個能適用於任意的矩陣的一種分解的方法：

    假設A是一個N * M的矩陣，那麼得到的U是一個N * N的方陣（裡面的向量是正交的，U裡面的向量稱為左奇異向量），Σ是一個N * M的矩陣（除了對角線的元素都是0，對角線上的元素稱為奇異值），V’(V的轉置)是一個N * N的矩陣，裡面的向量也是正交的，V裡面的向量稱為右奇異向量），從圖片來反映幾個相乘的矩陣的大小可得下面的圖片

    那麼奇異值和特徵值是怎麼對應起來的呢？首先，我們將一個矩陣A的轉置 * A，將會得到一個方陣，我們用這個方陣求特徵值可以得到：    這裡得到的v，就是我們上面的右奇異向量。此外我們還可以得到：

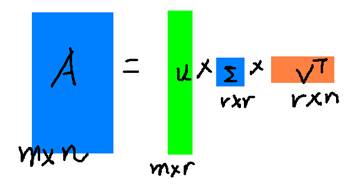
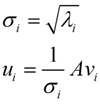    這裡的σ就是上面說的奇異值，u就是上面說的左奇異向量。奇異值σ跟特徵值類似，在矩陣Σ中也是從大到小排列，而且σ的減少特別的快，在很多情況下，前10%甚至1%的奇異值的和就佔了全部的奇異值之和的99%以上了。也就是說，我們也可以用前r大的奇異值來近似描述矩陣，這裡定義一下部分奇異值分解：

    r是一個遠小於m、n的數，這樣矩陣的乘法看起來像是下面的樣子：

    右邊的三個矩陣相乘的結果將會是一個接近於A的矩陣，在這兒，r越接近於n，則相乘的結果越接近於A。而這三個矩陣的面積之和（在儲存觀點來說，矩陣面積越小，儲存量就越小）要遠遠小於原始的矩陣A，我們如果想要壓縮空間來表示原矩陣A，我們存下這裡的三個矩陣：U、Σ、V就好了。

二、奇異值的計算：

    奇異值的計算是一個難題，是一個O(N^3)的演算法。在單機的情況下當然是沒問題的，matlab在一秒鐘內就可以算出1000 * 1000的矩陣的所有奇異值，但是當矩陣的規模增長的時候，計算的複雜度呈3次方增長，就需要平行計算參與了。Google的吳軍老師在數學之美系列談到SVD的時候，說起Google實現了SVD的並行化演算法，說這是對人類的一個貢獻，但是也沒有給出具體的計算規模，也沒有給出太多有價值的資訊。

    其實SVD還是可以用並行的方式去實現的，在解大規模的矩陣的時候，一般使用迭代的方法，當矩陣的規模很大（比如說上億）的時候，迭代的次數也可能會上億次，如果使用Map-Reduce框架去解，則每次Map-Reduce完成的時候，都會涉及到寫檔案、讀檔案的操作。個人猜測Google雲端計算體系中除了Map-Reduce以外應該還有類似於MPI的計算模型，也就是節點之間是保持通訊，資料是常駐在記憶體中的，這種計算模型比Map-Reduce在解決迭代次數非常多的時候，要快了很多倍。

    Lanczos迭代就是一種解對稱方陣部分特徵值的方法（之前談到了，解A’* A得到的對稱方陣的特徵值就是解A的右奇異向量），是將一個對稱的方程化為一個三對角矩陣再進行求解。按網上的一些文獻來看，Google應該是用這種方法去做的奇異值分解的。請見Wikipedia上面的一些引用的論文，如果理解了那些論文，也“幾乎”可以做出一個SVD了。

    由於奇異值的計算是一個很枯燥，純數學的過程，而且前人的研究成果（論文中）幾乎已經把整個程式的流程圖給出來了。更多的關於奇異值計算的部分，將在後面的參考文獻中給出，這裡不再深入，我還是focus在奇異值的應用中去。