排序演算法是演算法研究中最基礎的問題，本文針對排序演算法，介紹幾種排序演算法的基本方法、時間複雜度及Java實現等內容。

原址性 ：如果輸入陣列中僅有常數個元素需要在排序的過程中儲存在陣列之外，那麼排序演算法就是原址的。

　　　　　　　　常用排序演算法的執行時間比較

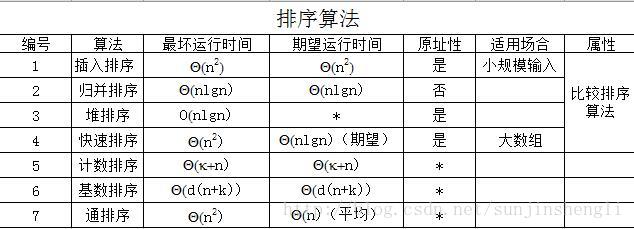
上表中，ｎ表示要排序資料項數量。對於計數排序，資料項均在集合｛０,１，．．．，ｋ｝內。對於基數排序，每個資料項都是ｄ位數字的整數，每位數字可能取ｋ個值。對於桶排序，假定關鍵字是半開區間［０，１）內服從均勻分佈的ｎ個實數。

一、插入排序

插入排序的思想就類似於我們玩牌，拿到手的是一把亂牌。我們從左到右排序。從第二張開始，我們與第一張比較，小的話就插到第一張前面。到後面某一張牌，我們會依次和前面的牌進行比較，直到比該牌小的位置，放到它的後面。
示例程式碼

public static void sortInsert(int[] n){
        //int count = 0;
        for(int i = 1; i < n.length; i++) {
            int key = n[i];
            int j = i - 1;
            while(j >= 0 && n[j] > key){
                n[j+1] = n[j];
                j--;
            }
            n[j+1
 
] = key;
            System.out.print(i + ":");
            for(int num: n)
                System.out.print(num + " ");
            System.out.println();
        }
    }

生成一個隨機陣列並進行插入排序，執行結果如下：
執行結果

E:\code\jv\alg0rithmOjava\排序>java InsertSort
35 58 24 75 77 17 73 64 66 88
1:35 58 24 75 77 17 73 64 66 88
2:24
 
 35 58 75 77 17 73 64 66 88
3:24 35 58 75 77 17 73 64 66 88
4:24 35 58 75 77 17 73 64 66 88
5:17 24 35 58 75 77 73 64 66 88
6:17 24 35 58 73 75 77 64 66 88
7:17 24 35 58 64 73 75 77 66 88
8:17 24 35 58 64 66 73 75 77 88
9:17 24 35 58 64 66 73 75 77 88
17 24 35 58 64 66 73 75 77 88

二、堆排序

堆排序通過“堆”資料結構進行排序，其時間複雜度是O(nlgn)，並具有空間原址性。結合了插入排序和歸併排序的優點。

1. 堆

（二叉）堆是一個數組，可以近似的看成一個完全二叉樹，樹上的每一個節點對應陣列中的一個元素。堆heap的陣列Array包括兩個屬性，一個是陣列的長度A.length，一個是堆的大小heap.size，並有 0 <= heap.size <= A.length。也就是說，陣列中的資料不一定都是堆的有效資料。
最大堆 ： 二叉堆又可以分為兩種形式：最大堆和最小堆。最大堆的父節點的資料要比子節點的都大，最小堆則是都要小。堆排序演算法中用的是最大堆，構造優先佇列一般用最小堆。
堆的高度 ： 一個堆節點的高度就是某節點到葉節點最長的簡單路徑的邊數。而堆的高度則對應根節點的高度。就是O(lgn).

2. 建堆

通過該示例，我們可以看出，對左右子樹都是最大堆的根節點維護最大堆的方法。
所以將一個普通的堆維護成最大堆的方法，就是從底到根依次維護一次。不過不難發現，最底層的節點是沒有子節點的，自然滿足最大堆。也就是應該從開始有子節點的節點處開始倒序遍歷維護節點。根據完全二叉樹的性質，這個節點就是 heap.size / 2.

實現程式碼

public void builtMaxHeapify(){

        for(int i = heapSize/2; i >= 0; i--) {
            MaxHeapify(i);
        }
    }

    public void exchange(int i, int j) {
        heapArray[i] = heapArray[i] + heapArray[j];
        heapArray[j] = heapArray[i] - heapArray[j];
        heapArray[i] = heapArray[i] - heapArray[j];
    }

    public void MaxHeapify(int i) {
        int largest = i;
        int l = (i + 1) << 1;
        int r = l + 1;
        if( l <= heapSize && heapArray[l-1] > heapArray[i])
            largest = l-1;
        else 
            largest = i;
        if( r <= heapSize && heapArray[r -1] > heapArray[largest])
            largest = r-1;
        if(largest != i){
            heapArray[i] = heapArray[i] + heapArray[largest];
            heapArray[largest] = heapArray[i] - heapArray[largest];
            heapArray[i] = heapArray[i] - heapArray[largest];
            MaxHeapify(largest);
        }
    }
}

執行結果

>java Test
18 26 66 75 1 53 47 80 47 71
80 75 66 47 71 53 47 26 18 1
1 75 66 47 71 53 47 26 18 80
75 71 66 47 1 53 47 26 18
18 71 66 47 1 53 47 26 75
71 47 66 26 1 53 47 18
18 47 66 26 1 53 47 71
66 47 53 26 1 18 47
47 47 53 26 1 18 66
53 47 47 26 1 18
18 47 47 26 1 53
47 26 47 18 1
1 26 47 18 47
47 26 1 18
18 26 1 47
26 18 1
1 18 26
18 1
1 18
1
1 18 26 47 47 53 66 71 75 80