原理和C++實現的演示程式(附原始碼)
http://blog.csdn.net/mahabharata_/article/details/71856907
大二的時候,曾受老師所託,用C++而不是OpenGL去寫B樣條曲線的教學程式。時隔一年,發現原始碼找不見了,所以重新寫了一遍,也完善了部分功能,順便發一篇部落格分享一下。
這裡給出的資源有:兩個打包程式、最新版本的原始碼。
下載連結:(使用時請註明出處哦~~ )
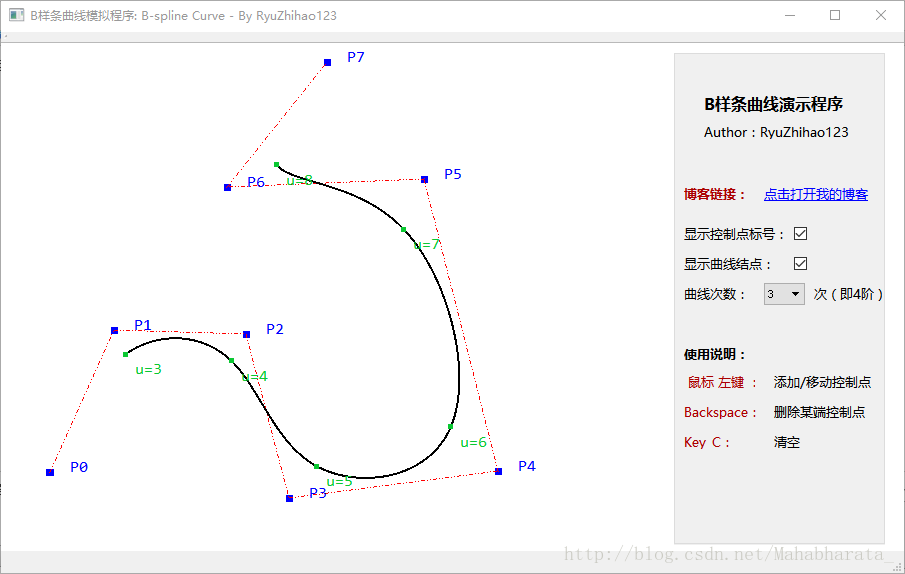
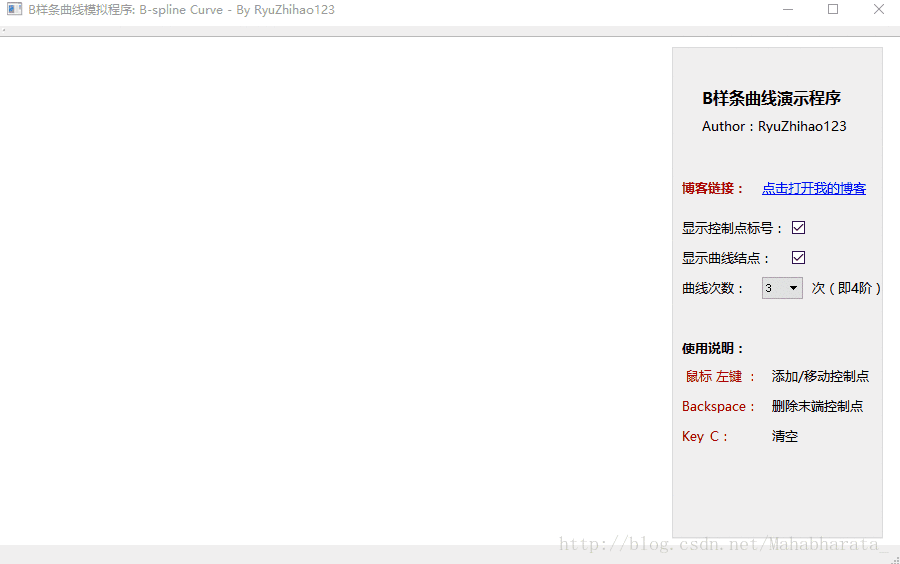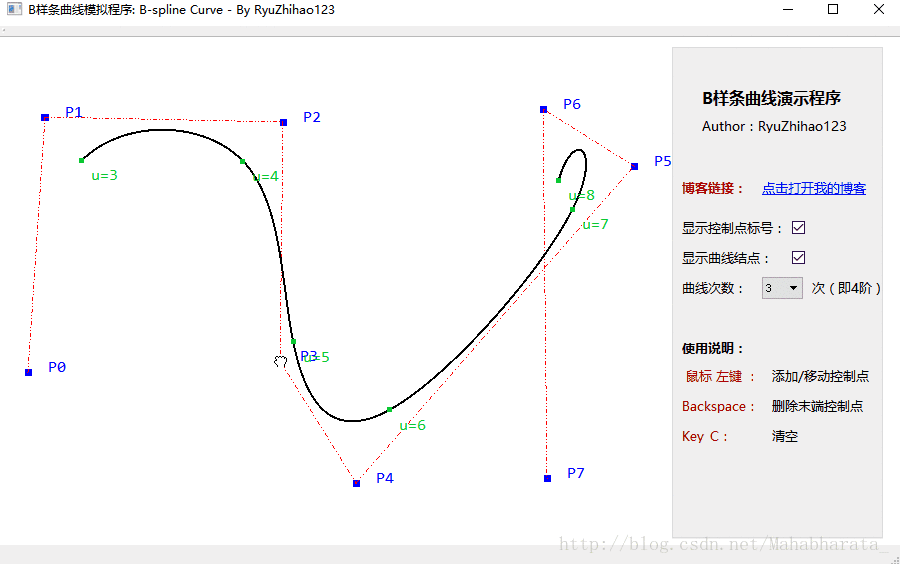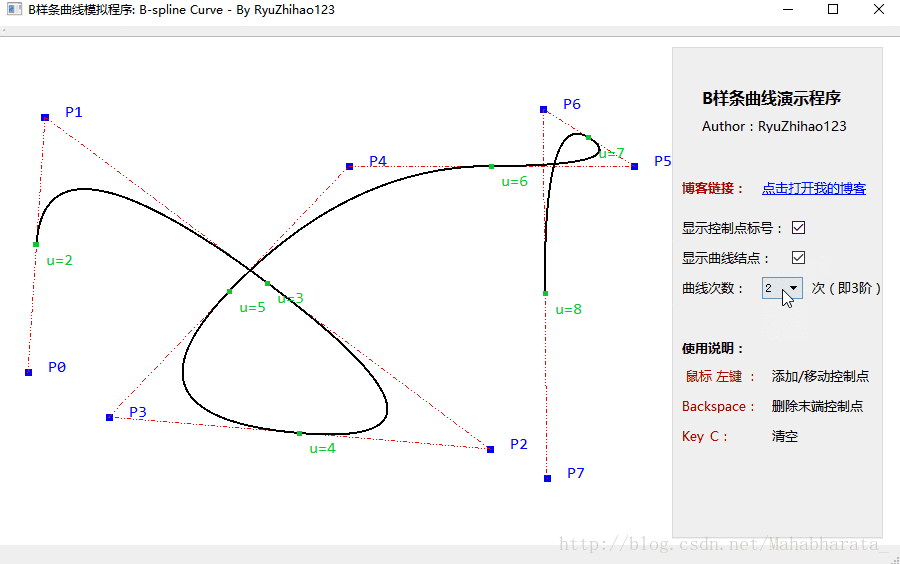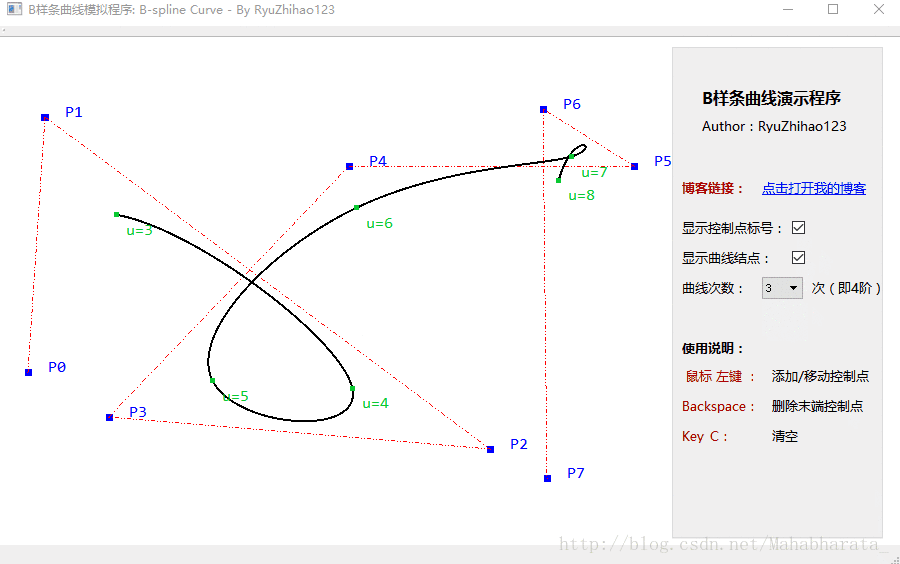
程式的截圖如下:
說明: 兩個版本都是使用純Qt實現的,沒有使用OpenGL所以非常方便閱讀。如需要使用win32、MFC等框架編寫,也只需在此基礎上做簡單的修改。
功能:
1. 滑鼠左鍵可以新增新控制點,也可以選中並拖動已有的控制點。
2. 支援1次、2次、3次的B-Spline曲線(即2階、3階、4階)
3. 可以選擇是否顯示曲線上關鍵結點的位置和標號,以及控制點的標號。
4. Backspace刪除末端控制點,C鍵清屏。
B樣條曲線的相關知識:
定義:給定n+1個控制點{P0、P1、......、Pn},每個控制點都有對應的一個基函式Ni,p(u),其中u為自變數,i為第i個結點,p為曲線的次數(次數=階數-1),則可以用下式來定義B樣條曲線:

(定義域: p≤ u ≤ n+1,事實上定義域的上限取多少無所謂)
根據定義,可以發現B樣條曲線上的每一個點其實是:所有控制點的一個加權平均。這裡的“權”由基函式Ni,p(u)確定。隨著u從下限p逐漸增長,控制點對應的基函式的取值也會隨之變化,從而產生曲線上新的點。
關於基函式Ni,p(u),可以由Cox-de Boor公式得出。這裡給出三個簡單的基函式的示例:
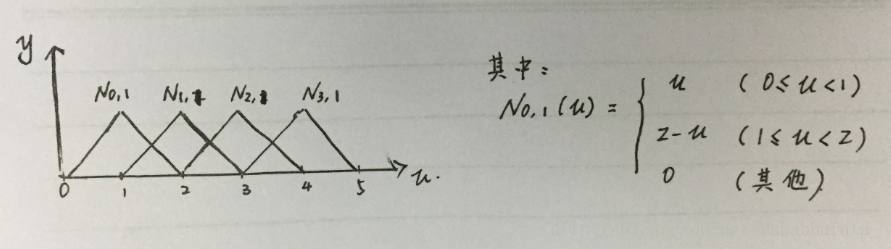
(1)當曲線次數p=1時,基函式Ni,1(u)為:
(2)當曲線次數p=2時,基函式Ni,2(u)為:
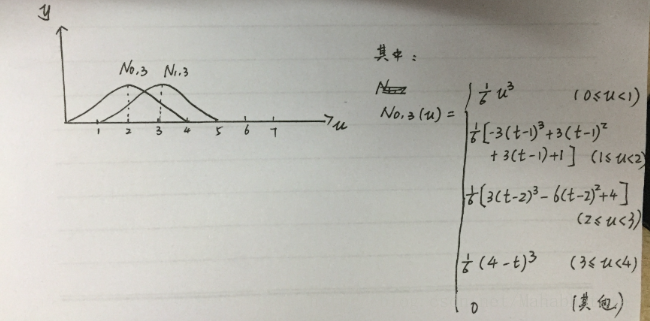
(3)當曲線次數p=3時,基函式Ni,3(u)為: