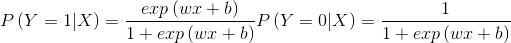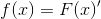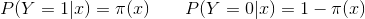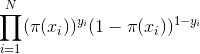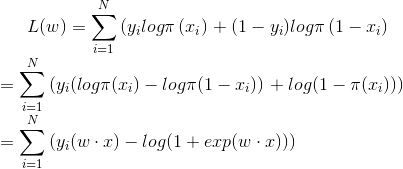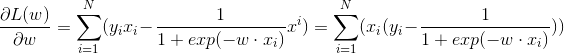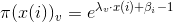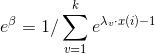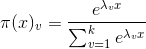邏輯斯蒂迴歸原理篇
1.邏輯斯蒂迴歸模型
LR模型主要用於分類模型,細心的人不難發現LR模型線上性迴歸模型上加了一個sigmoid轉換。為了更加深入地瞭解這個模型,我們可能要思考以下幾個問題
(1)sigmoid從何而來,篇幅比較大,下面會單獨討論
(2)sigmoid轉換的優勢
- 求梯度方便
- 資料統一分佈在0-1之間,從下面的LR分佈也可以看出
(3)這種轉換需要注意的地方,LR分佈可以此種轉換的特徵
2.邏輯斯蒂迴歸分佈
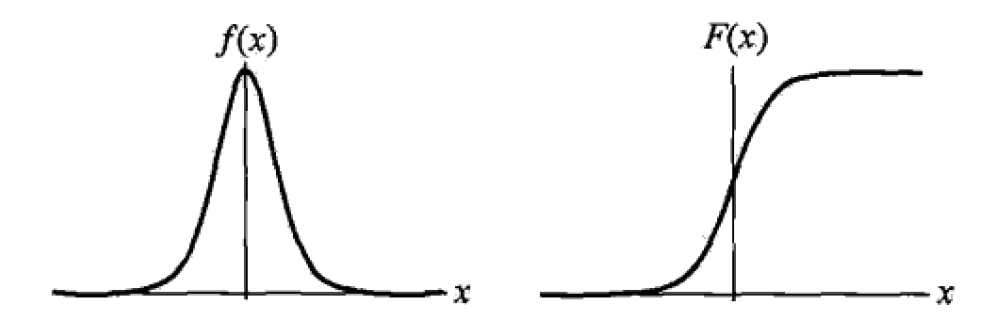
分佈函式
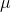
密度函式
邏輯斯蒂迴歸分佈的密度函式和分佈函式
不難看出,F(x)曲線在中心附近增長速度比較快,在兩端增長速度較慢。形狀引數
3.模型引數估計
應用極大似然估計法估計模型
(1)設
(2)似然函式
(3)對數似然函式
(4)梯度下降
最後括號中表達式就是訓練時的誤差,從而我們可以通過batch等方法進行隨機梯度下降
4.揭祕sigmoid
定義表示式
A(u,v):如果u == v,則A(u,v) = 1 ,否則為0
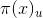
滿足條件
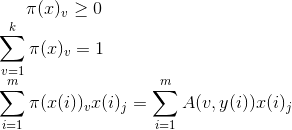
第三個條件可以簡單的從頻率學派和貝葉斯學派理解
優化目標(拉格朗日)
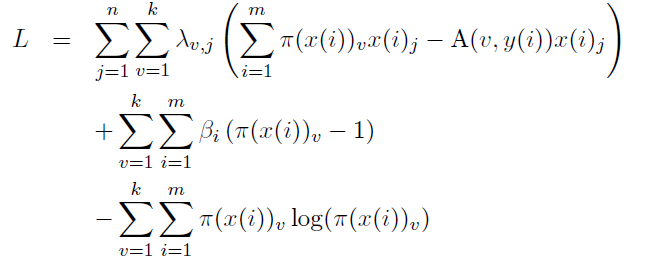
求梯度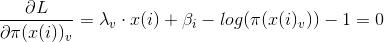
最終可以得到
對於分類問題,我們最終要確保每個類別概率之和為1
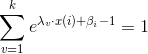
因此
通過化簡可得
5.在二分類問題中,為什麼棄用傳統的線性迴歸模型,改用邏輯斯蒂迴歸?
線性迴歸用於二分類時,首先想到下面這種形式,p是屬於類別的概率:
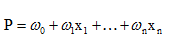
但是這時存在的問題是:
1)等式兩邊的取值範圍不同,右邊是負無窮到正無窮,左邊是[0,1],這個分類模型的存在問題
2)實際中的很多問題,都是當x很小或很大時,對於因變數P的影響很小,當x達到中間某個閾值時,影響很大。即實際中很多問題,概率P與自變數並不是直線關係。
所以,上面這分類模型需要修整,怎麼修正呢?統計學家們找到的一種方法是通過logit變換對因變數加以變換,具體如下:
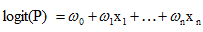
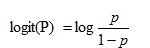
從而,
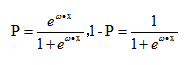
這裡的P完全解決了上面的兩個問題。
6.從最根本的廣義線性模型角度,匯出經典邏輯迴歸
1)指數家族
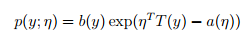
當固定T時,這個分佈屬於指數家族中的哪種分佈就由a和b兩個函式決定。下面這種是伯努利分佈,對應於邏輯迴歸問題
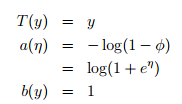
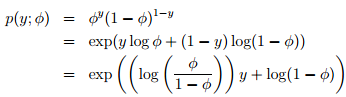
注:從上面可知
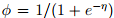
下面這種是高斯分佈,對應於經典線性迴歸問題
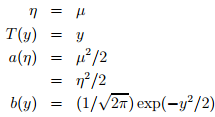
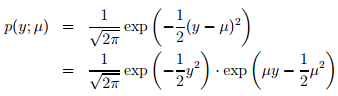
2)GLM(廣義線性模型)
指數家族的問題可以通過廣義線性模型來解決。如何構建GLM呢?在給定x和引數後,y的條件概率p(y|x,θ) 需要滿足下面三個假設:
assum1) y | x; θ ∼ ExponentialFamily(η).
assum2) h(x) = E[y|x]. 即給定x,目標是預測T(y)的期望,通常問題中T(y)=y
assum3) η = θTx,即η和x之間是線性的
3)經典邏輯迴歸
邏輯迴歸:以二分類為例,預測值y是二值的{1,0},假設給定x和引數,y的概率分佈服從伯努利分佈(對應構建GLM的第一條假設)。由上面高斯分佈和指數家族分佈的對應關係可知,,根據構建GLM的第2、3條假設可model表示成:
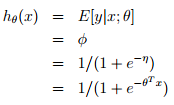
可以從GLM這種角度理解為什麼logistic regression的公式是這個形式~
7.實戰體驗
二分類問題,分類邊界實乃重中之重。訓練樣本是否均衡、樣本權重都會對邊界有影響
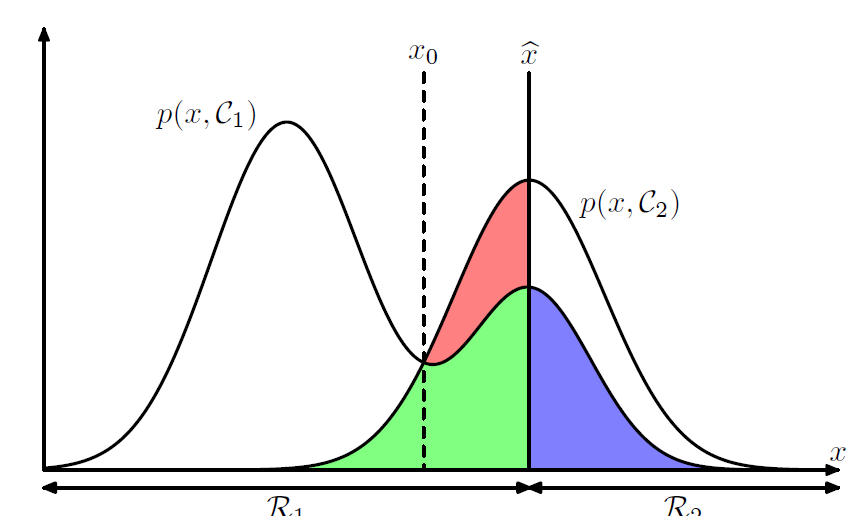
C1、C2為類別,圖片引用於PRML
瞭解下Fisher判別函式對理解分類問題本質會有很大幫助
8.多項邏輯斯蒂迴歸
假設離散型隨機變數Y的取值集合是{1,2…,K},那麼多項邏輯斯蒂迴歸模型是
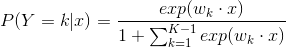
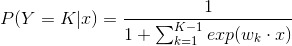
類似於CNN分類最後一層softmax
9.Tip
- 訓練速度快
- 資料量比較少的時候容易過擬合,這與使用極大似然估計(本質上為均值)是有關的
- 特徵One-hot
- 設計組合特徵
- 進行多分類的時候,思考下不同label之間是否有關係,從而覺得到底使用多個二分類還是一個多分類