1）基本概念

我們先從最基本的一些概念入手。

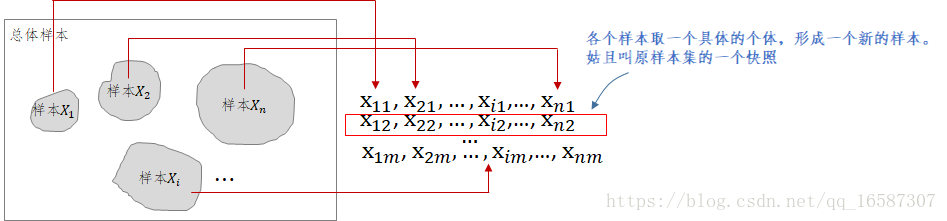
如下圖，腦子裡要浮現出總體樣本，還有一系列隨機選取的樣本。只要是樣本，腦子裡就要浮現出它的集合屬性，它不是單個個體，而是一堆隨機個體集合。樣本是總體樣本中隨機抽取一系列個體組成的集合，它是總體樣本的一部分。

應該把樣本和總體樣本一樣進行抽象化理解，因此樣本也存在期望和方差。

這裡有一個重要的假設，就是隨機選取的樣本與總體樣本同分布，它的意思就是說他們的統計特性是完全一樣的，即他們的期望值一樣，他們的方差值也是一樣的：

另外，由於每個樣本的選取是隨機的，因此可以假設不相關(意味著協方差為0，即)，根據方差性質就有:

另外，還需要知道方差另外一個性質：

為常數。

還有一個，別忘了方差的基本公式：

以上的公式都很容易百度得到，也非常容易理解。這裡不贅述。

2）無偏估計

接下來，我們來理解下什麼叫無偏估計。

定義：設統計量是總體中未知引數的估計量，若，則稱為的無偏估計量；否則稱為有偏估計量。

上面這個定義的意思就是說如果你拿到了一堆樣本觀測值，然後想通過這一堆觀測值去估計某個統計量，一般就是想估計總體的期望或方差，如果你選擇的方法所估計出來的統計量的平均值與總體樣本的統計量相等，那麼我們稱這種方法下的估計量是無偏估計，否則，就稱這種方法下的估計量為有偏估計量。

按照這麼理解，那麼有偏無偏是針對你選擇估計的方法所說的，它並不是針對具體某一次估計出來的估計量結果。如果方法不對，即使你恰好在某一次計算出來一個值和總體樣本統計量值相同，也並不代表你選的這個方法是無偏的。為什麼呢？這是因為單次

3）樣本均值的無偏估計

接下來探討一下下面的定義：

定義：樣本均值是總體樣本均值的無偏估計。

注意：這裡樣本均值不是指某個樣本的均值。

這裡需要看上面這張圖，這裡的均指的是特定某次樣本集合的快照（上圖紅色框）,顯然這個快照也是一個樣本，只不過這個樣本它的樣本大小固定為n，這與抽象的樣本不一樣（一般我們想象抽象的樣本，比如，是無限大的）。

明顯，

第一個樣本(快照)均值是長這樣子的：

第二個樣本(快照)均值是長這樣子的：

....依此類推...

表示第次隨機從從本獲取一個個體。

試驗一直進行下去，你就會有一些列估計出來的樣本(快照)均值，實際上這也稱為了一個樣本，我們稱為均值的樣本，既然是樣本，它就也有統計量。我們這裡重點關注這個均值樣本的期望。因為按照估計量的有偏無偏定義，如果，那麼按照這個方法估計的均值就是無偏的。仔細思考，估計量有偏無偏它是針對你所選定的某個估計方法所形成的估計量樣本空間來討論的，討論單次試驗形成的估計量是沒有太大意義的，只有針對形成的估計量樣本空間才有意義。

下面驗證上面的方法形成的估計是無偏的。

這麼一來，就和教科書和網上的資料結果上都對上了，教科書上的公式在下面列出（符號用代替）：

有了前面的分析，上面的教科書公式就很好理解了，注意，裡頭的是原始樣本，也是樣本!!!  公式推導過程中，表示了原始的樣本快照求和後再除以n形成的估計量樣本，所以是可以對其再進行求期望的。

討論完估計量樣本的均值，我們別忘了，既然它是個樣本，那麼可以計算的方差（後面會用到）:

所以，樣本（快照）均值的均值還是總體均值，但是，樣本（快照)均值的方差卻不是原來的方差了，它變成原來方差的1/n。這也容易理解，方差變小了是由於樣本不是原來的樣本了，現在的樣本是均值化後的新樣本，既然均值化了，那麼比起原來的老樣本，它的離散程度顯然是應當變小的。

4）樣本方差的無偏估計

定義：樣本方差是總體樣本方差的無偏估計。

也就是需要證明下面的結論：

首先，腦子裡要非常清楚，你截至目前，僅僅知道以下內容：

其中前面5個來自1），最後2個來自3)。

至於為什麼是，而不是，需要看下面的證明。

那麼為什麼會導致這麼個奇怪的結果，不是而是  ？

仔細看上面的公式，如果，那麼就應該是了，但是殘酷的事實是（除非本身就等於0），導致的罪魁禍首是。這就有告訴我們，雖然將方差縮小了n倍，但是仍然還有殘存，除非本身就等於0，才會有，但這就意味著所有樣本的個體處處等於。

還有一種情況，如果你事先就知道，那麼就是的無偏估計，這個時候就是了。