“只要不是特別大的記憶體開銷，時間複雜度比較重要。因為改進時間複雜度對演算法的要求更高。”
——吳斌（NVidia，Graphics Architect）

同樣是查詢，如果是順序查詢需要O（n）的時間；如果輸入的是排序的陣列則只需要O（logn）的時間；如果事先已經構造好了雜湊表，那查詢在O（1）時間就能完成。我們只有對常見的資料結構和演算法都瞭然於胸，才能在需要的時候選擇合適的資料結構和演算法來解決問題。

面試題29：陣列中出現次數超過一半的數字

題目：陣列中有一個數字出現的次數超過陣列長度的一半，請找出這個數字。例如輸入一個長度為9的陣列{1,2,3,2,2,2,5,4,2}。由於數字2在陣列中出現了5次，超過陣列長度的一半，因此輸出2。

看到這道題很多應聘者就會想要是這個陣列是排序的陣列就好了。如果是排好序的陣列，那麼我們就能很容易統計出每個數字出現的次數。題目給出的陣列沒有說是排序的，因此我們需要先給它排序。排序的時間複雜度是O（nlogn）。最直觀的演算法通常不是面試官滿意的演算法，接下來我們試著找出更快的演算法。

解法一：基於Partition函式的O（n）演算法

如果我們考慮到陣列的特性：陣列中有一個數字出現的次數超過了陣列長度的一半。如果把這個陣列『排序』，那麼排序之後位於陣列中間的數字一定就是那個出現次數超過陣列長度一半的數字。也就是說，這個數字就是統計學上的『中位數』，即長度為n的陣列中第n/2大的數字。我們有成熟的O（n）的演算法得到陣列中任意第k大的數字。

快速排序的實現

在這一段很迷惑，是因為需要好好考慮下如何實現在 O(n) 的演算法複雜度中找到任意第 k 大的數。『快速排序』第一趟排序之後，我們的到了一箇中間索引（我們暫且稱為 index），那麼排在中間 index 前面的值都比 array[index] 小；同樣的排序在中間 index 後面的元素都比 array[index] 大。第一趟的時間複雜度為O(n/2)。排序完之後，我們獲得了兩個子序列，同樣根據上述的邏輯進行排序，假設當 k < index 時，那麼我們就繼續排序第二段比 index 小的部分。這一次的時間複雜度為O(n/4)。以此類推，當我們把 index 定位到 k

	void QuickSort(int[] data, int length, int start, int end) {
		if (start == end) {
			return;
		}
		int index = Partition(data, length, start, end);
		if (index > start) {
			QuickSort(data, length, start, index - 1);
		}
		if (index < end) {
			QuickSort(data, length, index + 1, end);
		}
	}

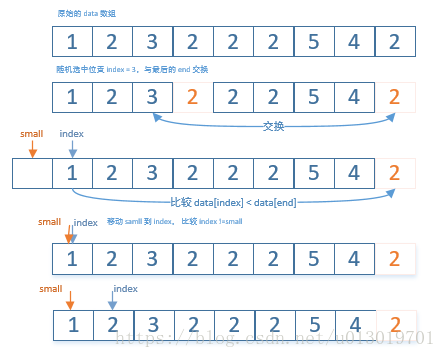
實現快速排序演算法的『關鍵』在於先在陣列中選擇一個數字（選中的數字，和返回的數字通常是不一樣的），接下來把陣列中的數字分為兩部分，比選擇的數字小的數字移到陣列的左邊，比選擇的數字大的數字移到陣列的右邊。這個函式可以如下實現：

	int Partition(int[] data, int length, int start, int end) {
		if (data == null || length <= 0 || start < 0 || end > length) {
			throw new RuntimeException("錯誤的引數");
		}
		// 從  start 到 end 之間，隨機選取一個整數
		int index = new Random().nextInt(end - start) + start;
		swap(data, index, end);
		int small = start - 1;
		for (index = start; index < end; ++index) {
			if (data[index] < data[end]) {
				++small;
				if (small != index) {
					swap(data, index, small);
				}
			}
		}
		++small;
		swap(data, small, end);
		return small;
	}

	void swap(int[] array, int i, int j) {
		int tmp = array[i];
		array[i] = array[j];
		array[j] = tmp;
	}

上面程式碼的實現思路如下：

1. 使用 Random 函式隨機生成一個 index，得到一個隨機的『中間參考值』，將該值換到函式的末尾。
2. 從頭到尾遍歷陣列，將陣列中，所有小於中間參考值的元素排在陣列的前面，small 記錄已經確定小於中間參考的下標
3. 返回 small 並且，換回末尾的中間參考值。
4. 一趟排序下來，在 small 索引前面的元素，都比 data[index] 小。

還有一種快速排序的實現是分別的從左往右查詢小於『中間參考值』的元素，和右往左查詢大於『中間參考值』的元素，進行交換，同樣可以達到快速排序的目的。參考的程式碼如下：

   /**
	 * <b>快速排序</b>
	 * <p>在陣列中找一個元素(節點)，比它小的放在節點的左邊，比它大的放在節點右邊。不斷執行這個操作….</p>
	 *
	 * @param array
	 * @return
	 */
	static String quickSort(int[] array) {
		if (array.length <= 0) {
			return null;
		}
		quickSort(array, 0, array.length - 1);
		return Arrays.toString(array);
	}

	/**
	 * 快速排序使用遞迴可以很好的實現，程式碼的邏輯結構如下。
	 * <p>1. 隨機的獲取一個用於比較的<b>中間值</b>，通常區中間的元素 <br>
	 * 2. 從前往後和從後往前分別查詢比<b>中間值</b>大的元素和小的元素，進行交換<br>
	 * 3. 直到確定不存在，交換元素，則<b>中間值</b>元素的兩邊就能確比</p>
	 *
	 * @param array
	 * @param left
	 * @param right
	 */
	static void quickSort(int[] array, int left, int right) {
		int i = left;
		int j = right;
		//支點: 可以取任意值（但通常選取位置中間）相對來說交換次數會比較小
		int pivot = array[(left + right) / 2];

		//左右兩端進行掃描，只要兩端還沒有交替，就一直掃描
		while (i <= j) {
			//尋找直到比支點大的數
			while (pivot > array[i])
				i++;

			//尋找直到比支點小的數
			while (pivot < array[j])
				j--;

			//此時已經分別找到了比支點小的數(右邊)、比支點大的數(左邊)，它們進行交換
			if (i <= j) {
				int temp = array[i];
				array[i] = array[j];
				array[j] = temp;
				i++;
				j--;
			}
		}
		//上面一個while保證了第一趟排序支點的左邊比支點小，支點的右邊比支點大了。

		//“左邊”再做排序，直到左邊剩下一個數(遞迴出口)
		if (left < j)
			quickSort(array, left, j);

		//“右邊”再做排序，直到右邊剩下一個數(遞迴出口)
		if (i < right)
			quickSort(array, i, right);
	}

雖然實現兩種實現方式不同，但是總體思路是一致的。

小提示：如果面試題是要求在排序的陣列（或者部分排序的陣列）中查詢一個數字或者統計某個數字出現的次數，我們都可以嘗試用『二分查詢』演算法。

迴歸到本題的思路

這種演算法是受『快速排序』演算法的啟發。在隨機快速排序演算法中，我們先在陣列中隨機選擇一個數字，然後調整陣列中數字的順序，使得比選中的數字小數字都排在它的左邊，比選中的數字大的數字都排在它的右邊。如果這個選中的數字的下標剛好是n/2，那麼這個數字就是陣列的中位數。如果它的下標大於n/2，那麼中位數應該位於它的左邊，我們可以接著在它的左邊部分的陣列中查詢。如果它的下標小於n/2，那麼中位數應該位於它的右邊，我們可以接著在它的右邊部分的陣列中查詢。這是一個典型的遞迴過程，可以用如下程式碼實現：

int moreThanHalfNum(int[] array, int length){
	if(ChechInvalidArray(array, length)){
		return 0;
	}
	int middle = length >> 1;
	int start = 0;
	int end = length - 1;
	int index = Partition(array, length, start, end);
	// 尋找中位數
	while(index != middle){
		// 如果得到 index 大於中間值，則往前半部分查詢
		if(index > middle){
			end = index - 1;
			index = Partition(array, length, start, end);
		}else{
			start = index + 1;
			index = Partition(array, length, start, end);
		}
	}
	int result = array[middle];
	if(!CheckMoreThanHalf(array, length, result)){
		return 0;
	}
	return result;
}

上面的程式碼中，CheckInvalidArray 用來判斷輸入的陣列是不是無效的。下面程式碼將，使用一個全域性變數來表示輸入無效的情況。

// 全域性變數判斷陣列是否無效
boolean arrayInvalid = false;

boolean CheckInvalidArray(int[] array, int length){
	arrayInvalid = false;
	if(array == null && length <= 0){
		arrayInvalid = true;
	}
	return arrayInvalid;
}

而對於如何驗證，中位數是否為次數最多的元素，我們可以對其進行一下次數的統計。 CheckMoreThanHalf 函式的實現，如下：

boolean CheckMoreThanHalf(int[] array, int length, int number){
	int times = 0;
	for (int i = 0; i < length; i++) {
		if(array[i] = number){
			times++;
		}
	}
	boolean isMoreThanHalf = true;
	if(times * 2 <= length){
		arrayInvalid = true;
		isMoreThanHalf = false;
	}
	return isMoreThanHalf;
}

解法二：根據陣列特點找出O（n）的演算法

接下來我們從另外一個角度來解決這個問題。陣列中有一個數字出現的次數超過陣列長度的一半，也就是說它出現的次數比其他所有數字出現次數的和還要多。因此我們可以考慮在遍歷陣列的時候儲存兩個值：一個是陣列中的一個數字，一個是次數。

• 當我們遍歷到下一個數字的時候，如果下一個數字和我們之前儲存的數字相同，則次數加1；
• 如果下一個數字和我們之前儲存的數字不同，則次數減1。
• 如果次數為零，我們需要儲存下一個數字，並把次數設為1。

由於我們要找的數字出現的次數比其他所有數字出現的次數之和還要多，那麼要找的數字肯定是最後一次把次數設為1時對應的數字。基於上面的思路寫下的程式碼：

 public Integer moreThanHalfNum(int[] array) {
	if (array == null)
		return null;
	Integer number = null;
	int count = 0;
	Integer resultInteger = null;
	for (int i = 0; i < array.length; i++) {
		if (number == null) {
			number = array[i];
			count++;
		} else {
			if (array[i] != number)
				if (count == 0) {
					number = array[i];
					count = 1;
				} else
					count--;
			else
				count++;
		}
		if (count == 1)
			resultInteger = number;
	}
	if (checkMoreThanHalf(array, resultInteger))
		return resultInteger;
	else
		return null;
}

其實思路，還有很多，如果不是為了考慮效率，且統計較小的話可以直接的通過 HashMap 進行統計，得出最大的值。

據說帥哥靚女都關注了↓↓↓