ACM模板——強連通分量(Tarjan)
一、講解一
強連通定義:在有向圖G<V,E>中,對於點集V'∈V, 點集中的任意兩點都可達,則稱V'為強連通。
孤立的一個點也是一個強連通分量。
在巢狀的多個環時 : {所有環上的點}為一個強連通分量( 最小環就是每個孤立點)注意一定是滿足條件的最大點集。
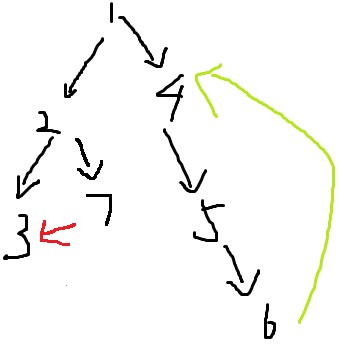
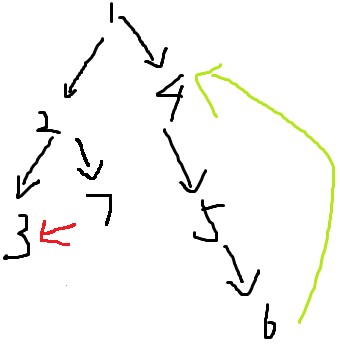
則上圖中強連通分量有 {1},{2},{3},{7},{4,5,6}。
tarjan的過程就是dfs過程:
對圖dfs一下,遍歷所有未遍歷過的點 ,會得到一個有向樹,顯然有向樹是沒有環的。(注意搜過的點不會再搜)
則能產生環的 只有(指向已經遍歷過的點)的邊。
如圖,只有紅色與綠色邊有可能產生環。
對於深搜過程,我們需要一個棧來儲存當前所在路徑上的所有點(棧中所有點一定是有父子關係的
再仔細觀察紅邊與綠邊,首先得到結論:紅邊不產生環,綠邊產生環
1、對於紅邊,連線的兩個點3、7沒有父子關係,這種邊稱為橫叉邊。橫叉邊一定不產生環。
2、對於綠邊,連線的兩個點6、4是父子關係,這種邊稱為後向邊。環一定由後向邊產生。
3、圖中除了黑色的樹枝邊,一定只有橫叉邊和後向邊。不存在其他種類的邊。
則以下考慮對於這兩種邊的處理和判斷,首先深搜會搜到這樣的圖:
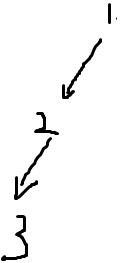
再次深搜:
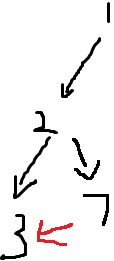
發現紅邊指向了已經遍歷過的點3 => 是上述的2種邊之一,而3不在棧中 => 3點與7點無父子關係。
=> 該邊為橫叉邊
=> 採取無視法
繼而7點退棧 產生連通分量{7}
繼而2點退棧 產生連通分量{2}
再次深搜:
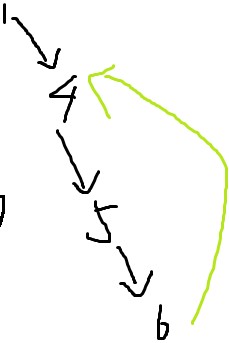
發現綠邊指向了已經遍歷過的點4 => 是上述的2種邊之一
而4在棧中 => 4點與6點是父子關係
=> 該邊為後向邊
=> 4->6 的路徑上的點都是環
int num[N], Top = 0; int u = Stack.top(); while(u!=4){ num[Top++] = u; Stack.pop(); u = Stack.top();} num[Top++] = u;
如此就能把Stack中 4->6 路徑上的點轉移到num數組裡。
顯然num陣列中的點是一個連通分量。
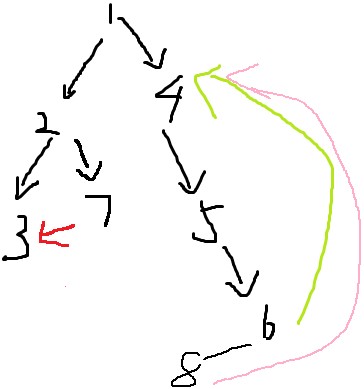
實際情況可能更復雜:
出現了大環套小環的情況,顯然我們認為最大環是一個強連通分量(即:{4,5,6,8} )。
二、講解二
全網最詳細tarjan演算法講解,我不敢說別的。反正其他tarjan演算法講解,我看了半天才看懂。我寫的這個,讀完一遍,發現原來tarjan這麼簡單!
tarjan演算法,一個關於圖的聯通性的神奇演算法。基於DFS(迪法師)演算法,深度優先搜尋一張有向圖。注意!是有向圖。根據樹,堆疊,打標記等種種神(che)奇(dan)方法來完成剖析一個圖的工作。而圖的聯通性,就是任督二脈通不通的問題。 瞭解tarjan演算法之前你需要知道: 強連通,強連通圖,強連通分量,解答樹(解答樹只是一種形式瞭解即可)
強連通(strongly connected): 在一個有向圖G裡,設兩個點 a b 發現,由a有一條路可以走到b,由b又有一條路可以走到a,我們就叫這兩個頂點(a,b)強連通。
強連通圖: 如果 在一個有向圖G中,每兩個點都強連通,我們就叫這個圖,強連通圖。
強連通分量strongly connected components):在一個有向圖G中,有一個子圖,這個子圖每2個點都滿足強連通,我們就叫這個子圖叫做 強連通分量 [分量::把一個向量分解成幾個方向的向量的和,那些方向上的向量就叫做該向量(未分解前的向量)的分量。
舉個簡單的栗子:
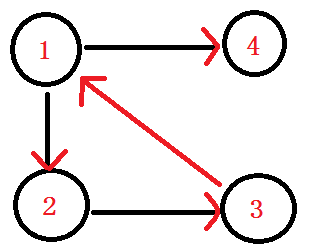
比如說這個圖,在這個圖中呢,點1與點2互相都有路徑到達對方,所以它們強連通。
而在這個有向圖中,點1 2 3組成的這個子圖,是整個有向圖中的強連通分量。
解答樹:就是一個可以來表達出遞迴列舉的方式的樹(圖),其實也可以說是遞迴圖。反正都是一個作用,一個展示從“什麼都沒有做”開始到“所有結求出來”逐步完成的“過程”!
tarjan演算法,之所以用DFS就是因為它將每一個強連通分量作為搜尋樹上的一個子樹。而這個圖,就是一個完整的搜尋樹。 為了使這顆搜尋樹在遇到強連通分量的節點的時候能順利進行,每個點都有兩個引數。 1、DFN[]作為這個點搜尋的次序編號(時間戳),簡單來說就是 第幾個被搜尋到的。// 每個點的時間戳都不一樣。 2、LOW[]作為每個點在這顆樹中的,最小的子樹的根,每次保證最小,like它的父親結點的時間戳這種感覺。如果它自己的LOW[]最小,那這個點就應該從新分配,變成這個強連通分量子樹的根節點。 Ps:每次找到一個新點,這個點 LOW[]=DFN[]。
而為了儲存整個強連通分量,這裡挑選的容器是,堆疊。每次一個新節點出現,就進站,如果這個點有 出度 就繼續往下找。直到找到底,每次返回上來都看一看子節點與這個節點的LOW值,誰小就取誰,保證最小的子樹根。如果找到DFN[]==LOW[]就說明這個節點是這個強連通分量的根節點(畢竟這個 LOW[]值是這個強連通分量裡最小的)最後找到強連通分量的節點後,就將這個棧裡,比此節點後進來的節點全部出棧,它們就組成一個全新的強連通分量。
先來一段虛擬碼壓壓驚:
tarjan(u){
DFN[u]=Low[u]=++Index // 為節點u設定次序編號和Low初值
Stack.push(u) // 將節點u壓入棧中
for each (u, v) in E // 列舉每一條邊
if (v is not visted) // 如果節點v未被訪問過
tarjan(v) // 繼續向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果節點u還在棧內
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果節點u是強連通分量的根
repeat v = S.pop // 將v退棧,為該強連通分量中一個頂點
print v
until (u== v)
}首先來一張有向圖。網上到處都是這個圖。我們就一點一點來模擬整個演算法。
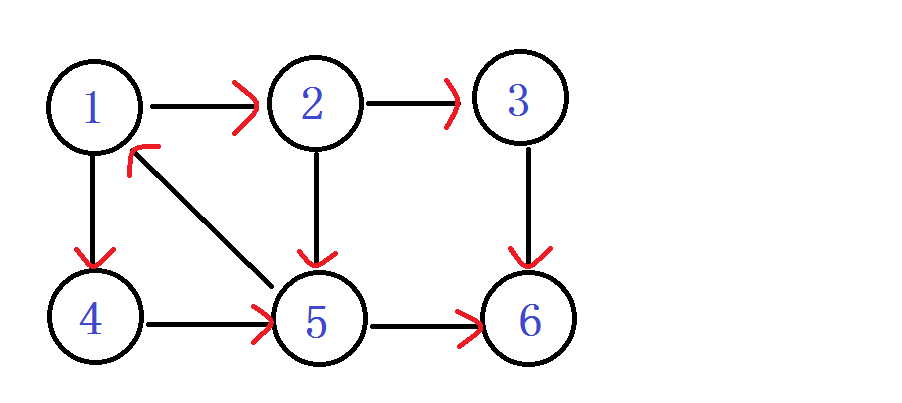
從1進入 DFN[1]=LOW[1]= ++index ----1 入棧 1 由1進入2 DFN[2]=LOW[2]= ++index ----2 入棧 1 2 之後由2進入3 DFN[3]=LOW[3]= ++index ----3 入棧 1 2 3 之後由3進入 6 DFN[6]=LOW[6]=++index ----4 入棧 1 2 3 6
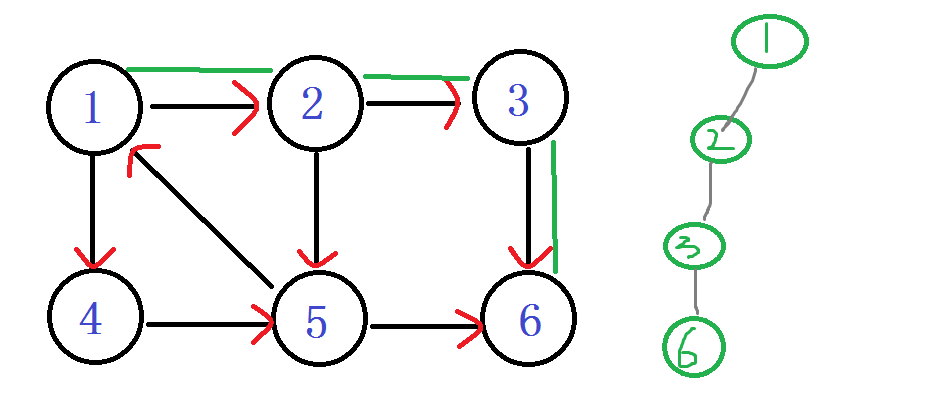
之後發現 嗯? 6無出度,之後判斷 DFN[6]== LOW[6] 說明6是個強連通分量的根節點:6及6以後的點 出棧。 棧: 1 2 3 之後退回 節點3 Low[3] = min(Low[3], Low[6]) LOW[3]還是 3 節點3 也沒有再能延伸的邊了,判斷 DFN[3]== LOW[3] 說明3是個強連通分量的根節點:3及3以後的點 出棧。 棧: 1 2 之後退回 節點2 嗯?!往下到節點5 DFN[5]=LOW[5]= ++index ----5 入棧 1 2 5
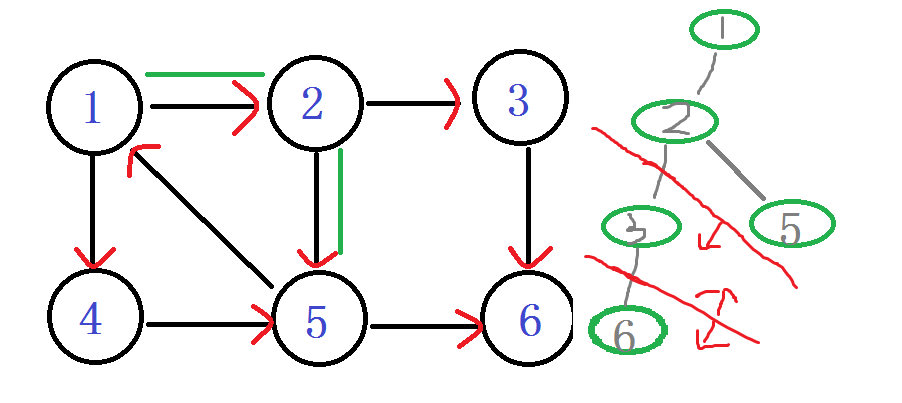
Ps:你會發現在有向圖旁邊的那個醜的(劃掉)搜尋樹 用紅線剪掉的子樹,那個就是強連通分量子樹。每次找到一個。直接一剪子下去,半個子樹就沒有了。
結點5 往下找,發現節點6 DFN[6]有值,被訪問過。就不管它。
繼續5 往下找,找到了節點1 他爸爸的爸爸。DFN[1]被訪問過並且還在棧中,說明1還在這個強連通分量中,值得發現。
Low[5] = min(Low[5], DFN[1])
確定關係,在這棵強連通分量樹中,5節點要比1節點出現的晚。所以5是1的子節點。
So LOW[5]= 1
由5繼續回到2 Low[2] = min(Low[2], Low[5])
LOW[2]=1;
由2繼續回到1 判斷 Low[1] = min(Low[1], Low[2])
LOW[1]還是 1
1還有邊沒有走過。發現節點4,訪問節點4
DFN[4]=LOW[4]=++index ----6
入棧 1 2 5 4
由節點4,走到5,發現5被訪問過了,5還在棧裡,
Low[4] = min(Low[4], DFN[5]) LOW[4]=5
說明4是5的一個子節點。
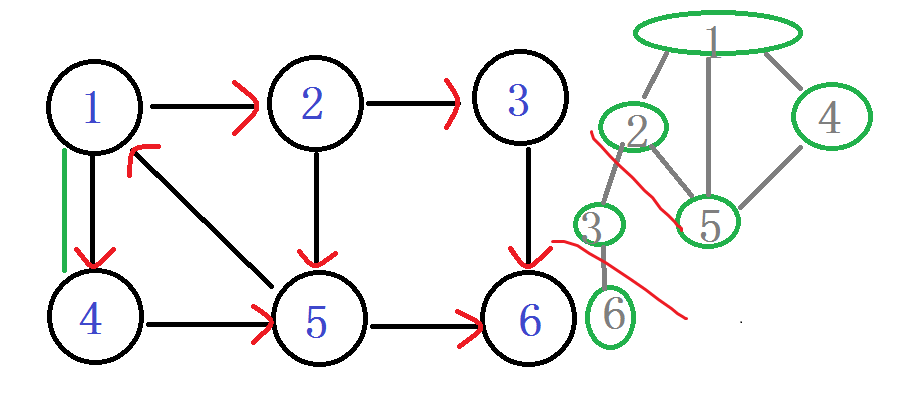
由4回到1
回到1,判斷 Low[1] = min(Low[1], Low[4])
LOW[1]還是 1 。
判斷 LOW[1] == DFN[1]
誒?!相等了 說明以1為根節點的強連通分量已經找完了。
將棧中1以及1之後進棧的所有點,都出棧。
棧 :(鬼都沒有了)
這個時候就完了嗎?!你以為就完了嗎?!
然而並沒有完,萬一你只走了一遍tarjan整個圖沒有找完怎麼辦呢?!
所以,tarjan的呼叫最好在迴圈裡解決。
like 如果這個點沒有被訪問過,那麼就從這個點開始tarjan一遍。
因為這樣好讓每個點都被訪問到。
來一道裸程式碼。
輸入:
一個圖有向圖。
輸出:
它每個強連通分量。
input:
6 8
1 3
1 2
2 4
3 4
3 5
4 6
4 1
5 6
Output:
6
5
3 4 2 1三、程式碼
#include<bits/stdc++.h>
#include<cmath>
#define mem(a,b) memset(a,b,sizeof a)
#define ssclr(ss) ss.clear(), ss.str("")
#define INF 0x3f3f3f3f
#define MOD 1000000007
using namespace std;
typedef long long ll;
const int maxm=1001, maxn=1001;
struct node
{
int v,next;
}edge[maxm<<1];
int dfn[maxn], low[maxn];
int Stack[maxn], head[maxn], vis[maxn], cnt, tot, idx;
void init()
{
mem(head,-1);
cnt=tot=idx=0;
}
void add(int x,int y)
{
edge[++cnt].next=head[x];
edge[cnt].v=y;
head[x]=cnt;
}
void tarjan(int x) // 代表第幾個點在處理,遞迴的是點
{
dfn[x]=low[x]=++tot; // 新進點的初始化
Stack[++idx]=x; // 進站
vis[x]=1; // 表示在棧裡
for(int i=head[x]; i!=-1; i=edge[i].next)
{
if(!dfn[edge[i].v]) // 如果沒訪問過
{
tarjan(edge[i].v); // 往下進行延伸,開始遞迴
low[x]=min(low[x],low[edge[i].v]); // 遞迴出來,比較誰是誰的兒子/父親,就是樹的對應關係,涉及到強連通分量子樹最小根的事情
}
else if(vis[edge[i].v]) // 如果訪問過,並且還在棧裡
{
low[x]=min(low[x],low[edge[i].v]); // 比較誰是誰的兒子/父親。就是連結對應關係
}
}
if(low[x]==dfn[x]) // 發現是整個強連通分量子樹裡的最小根
{
do
{
printf("%d ",Stack[idx]);
vis[Stack[idx--]]=0; // 必須要寫,否則的話,案例中的節點5應該是獨個強連通分量,就變成和節點3 4 2 1一起輸出了(由於節點6沒清空引起)
}
while(x!=Stack[idx+1]); // 出棧,並且輸出。
puts("");
}
}
int main()
{
init();
int n,m,x,y;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++) scanf("%d%d",&x,&y), add(x,y);
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i); // 當這個點沒有訪問過,就從此點開始。防止圖沒走完
return 0;
}解釋1 ==> low[x]=min(low[x],low[edge[i].v])
當vis成立時,發現下個點可能是最小根點v的存在,並且該點x也沒有其他邊了,更新low[x]=low[v],回溯時,傳遞更新x的父親節點為可能最小根的low[可能最小根v]。如果x還有其他邊,以及此時的可能最小根點v2比上次的v還要小,則覆蓋。
解釋2 ==> if(low[x]==dfn[x])
1、直到回溯到真正的最小根為止,輸出該環。 2、避免了該環的其他非最小根的點單飛出去。