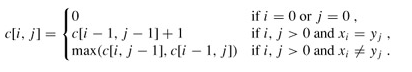看了幾分寫的相當好的部落格：

下面內容來轉載自上面文章

問題描述

什麼是最長公共子序列呢?好比一個數列 S，如果分別是兩個或多個已知數列的子序列，且是所有符合此條件序列中最長的，則S 稱為已知序列的最長公共子序列。

    舉個例子，如：有兩條隨機序列，如 1 3 4 5 5 ，and 2 4 5 5 7 6，則它們的最長公共子序列便是：4 5 5。

    注意最長公共子串（Longest CommonSubstring）和最長公共子序列（LongestCommon Subsequence, LCS）的區別：子串（Substring）是串的一個連續的部分，子序列（Subsequence）則是從不改變序列的順序，而從序列中去掉任意的元素而獲得的新序列；更簡略地說，前者（子串）的字元的位置必須連續，後者（子序列LCS）則不必。比如字串acdfg同akdfc的最長公共子串為df，而他們的最長公共子序列是adf。LCS可以使用動態規劃法解決。下文具體描述。

LCS問題的解決思路

窮舉法

 解最長公共子序列問題時最容易想到的演算法是窮舉搜尋法，即對X的每一個子序列，檢查它是否也是Y的子序列，從而確定它是否為X和Y的公共子序列，並且在檢查過程中選出最長的公共子序列。X和Y的所有子序列都檢查過後即可求出X和Y的最長公共子序列。X的一個子序列相應於下標序列{1, 2, …, m}的一個子序列，因此，X共有2m個不同子序列（Y亦如此，如為2^n），從而窮舉搜尋法需要指數時間（2^m * 2^n）。

動態規劃演算法

事實上，最長公共子序列問題也有最優子結構性質。

記：

Xi=﹤x1，⋯，xi﹥即X序列的前i個字元 (1≤i≤m)（字首）

Yj=﹤y1，⋯，yj﹥即Y序列的前j個字元 (1≤j≤n)（字首）

假定Z=﹤z1，⋯，zk﹥∈LCS(X , Y)。

    若xm=yn（最後一個字元相同），則不難用反證法證明：該字元必是X與Y的任一最長公共子序列Z（設長度為k）的最後一個字元，即有zk = xm = yn 且顯然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的字首Zk-1是Xm-1與Yn-1的最長公共子序列。此時，問題化歸成求Xm-1與Yn-1的LCS（LCS(X , Y)的長度等於LCS(Xm-1 , Yn-1)的長度加1）。

    若xm≠yn，則亦不難用反證法證明：要麼Z∈LCS(Xm-1, Y)，要麼Z∈LCS(X , Yn-1)。由於zk≠xm與zk≠yn其中至少有一個必成立，若zk≠xm則有Z∈LCS(Xm-1 , Y)，類似的，若zk≠yn 則有Z∈LCS(X , Yn-1)。此時，問題化歸成求Xm-1與Y的LCS及X與Yn-1的LCS。LCS(X , Y)的長度為：max{LCS(Xm-1 , Y)的長度, LCS(X , Yn-1)的長度}。

    由於上述當xm≠yn的情況中，求LCS(Xm-1 , Y)的長度與LCS(X , Yn-1)的長度，這兩個問題不是相互獨立的：兩者都需要求LCS(Xm-1，Yn-1)的長度。另外兩個序列的LCS中包含了兩個序列的字首的LCS，故問題具有最優子結構性質考慮用動態規劃法。

    也就是說，解決這個LCS問題，你要求三個方面的東西：1、LCS（Xm-1，Yn-1）+1；2、LCS（Xm-1，Y），LCS（X，Yn-1）；3、max{LCS（Xm-1，Y），LCS（X，Yn-1）}。

    行文至此，其實對這個LCS的動態規劃解法已敘述殆盡，不過，為了成書的某種必要性，下面，我試著再多加詳細闡述這個問題。

動態規劃演算法解LCS問題

1、最長公共子序列的結構

    最長公共子序列的結構有如下表示：

    設序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一個最長公共子序列Z=<z1, z2, …, zk>，則：

    若xm=yn，則zk=xm=yn且Zk-1是Xm-1和Yn-1的最長公共子序列；     若xm≠yn且zk≠xm ，則Z是Xm-1和Y的最長公共子序列；     若xm≠yn且zk≠yn ，則Z是X和Yn-1的最長公共子序列。

    其中Xm-1=<x1, x2, …, xm-1>，Yn-1=<y1, y2, …, yn-1>，Zk-1=<z1, z2, …, zk-1>。

2.子問題的遞迴結構

    由最長公共子序列問題的最優子結構性質可知，要找出X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最長公共子序列，可按以下方式遞迴地進行：當xm=yn時，找出Xm-1和Yn-1的最長公共子序列，然後在其尾部加上xm(=yn)即可得X和Y的一個最長公共子序列。當xm≠yn時，必須解兩個子問題，即找出Xm-1和Y的一個最長公共子序列及X和Yn-1的一個最長公共子序列。這兩個公共子序列中較長者即為X和Y的一個最長公共子序列。

    由此遞迴結構容易看到最長公共子序列問題具有子問題重疊性質。例如，在計算X和Y的最長公共子序列時，可能要計算出X和Yn-1及Xm-1和Y的最長公共子序列。而這兩個子問題都包含一個公共子問題，即計算Xm-1和Yn-1的最長公共子序列。

    與矩陣連乘積最優計算次序問題類似，我們來建立子問題的最優值的遞迴關係。用c[i,j]記錄序列Xi和Yj的最長公共子序列的長度。其中Xi=<x1, x2, …, xi>，Yj=<y1, y2, …, yj>。當i=0或j=0時，空序列是Xi和Yj的最長公共子序列，故c[i,j]=0。其他情況下，由定理可建立遞迴關係如下：

上面得出狀態轉換公式，也是下面填表和程式實現的依據。

在填充單元格時，需要考慮以下條件：

• 它左側的單元格
• 它上面的單元格
• 它左上側的單元格

這種方法的思路是：將從上向下、從左到右填充表格。（類似於非常經典的動態規劃——揹包問題的填表）

 請注意，我在圖中還添加了箭頭，指向當前單元格值的來源。

模板程式碼：

LCS長度

void lcsLength(string x,string y, vector< vector<int>> &c, vector< vector<char>> &b) {     int m = x.size();     int n = y.size();     c.resize(m+1);     b.resize(m+1);     for(int i = 0; i < c.size(); ++i)         c[i].resize(n+1);     for(int i = 0; i < b.size(); ++i)         b[i].resize(n+1);

    for(int i = 1; i <= m; ++i){         for(int j = 1; j <= n; ++j){             if(x[i-1] == y[j-1]){                 c[i][j] = c[i-1][j-1]+1;                 b[i][j] = 'c';             }else if(c[i-1][j] >= c[i][j-1]){                 c[i][j] = c[i-1][j];                 b[i][j] ='u';             }else{                 c[i][j] = c[i][j-1];                 b[i][j] = 'l';             }         }     } }

LCS的遞迴列印：

void print_lcs(vector< vector<char>> &b,string x, int i, int j) {     if(i == 0 || j == 0)         return;     if(b[i][j] == 'c'){         print_lcs(b,x,i-1,j-1);         cout << x[i-1];     }else if(b[i][j] == 'u')         print_lcs(b,x,i-1,j);     else         print_lcs(b,x,i,j-1); }

LCS的非遞迴列印（也可以用棧進行實現）：

char c[1010];         while(m > 0 && n > 0)//從終點按標記的方向反方向往回走         {             if(flag[m][n] == 1){ //這個方向來的元素包含在最長公共子序列中                 c[k++] = a[m - 1];                 m--; n--;             }             else if(flag[m][n] == 2)                 m--;             else if(flag[m][n] == 3)                 n--;         }         for(i = k-1;i >= 0;i--)             printf("%c",c[i]);         printf("\n");

LCS程式碼模板合成：

//LCS(longest common subsequence) 最長公共子序列演算法
//dacao
//2018/10/21

#include<iostream>
#include<vector>
#include<stack>
using namespace std;

void LCS_length(string x,string y,vector<vector<int> >&dp,vector<vector<char> > &flag)
{
	int m=x.length();
	int n=y.length();
	dp.resize(m+1);
	flag.resize(m+1);
	int i,j;
	for(i=0;i<dp.size();i++)
		dp[i].resize(n+1);
	for(i=0;i<flag.size();i++)
		flag[i].resize(n+1);
		
	for(i=1;i<=m;i++)
	{
		for(j=1;j<=n;j++)
		{
			if(x[i-1]==y[j-1])
			{
				dp[i][j]=dp[i-1][j-1]+1;
				flag[i][j]='c';
			}
			else if(dp[i-1][j] >= dp[i][j-1])
			{
				dp[i][j]=dp[i-1][j];
				flag[i][j]='u';//來源於上面 
			}
			else
			{
				dp[i][j]=dp[i][j-1];
				flag[i][j]='l';//來源於左邊 
			}
		}
	}
}

void dp_print_lcs(vector<vector<char> > &flag,string &x,int i,int j)
{
	if(i==0||j==0)
		return;
	if(flag[i][j]=='c')
	{
		dp_print_lcs(flag,x,i-1,j-1);
		cout<<x[i-1];
	}
	else if(flag[i][j]=='u')
		dp_print_lcs(flag,x,i-1,j);
	else
		dp_print_lcs(flag,x,i,j-1);
} 

void stack_print_lcs(vector<vector<char> > &flag,string &x,int i,int j)
{
	stack<char> ans;
	while(i>0&&j>0)//入棧 
	{
		if(flag[i][j]=='c')
		{
			ans.push(x[i-1]);
			i--;
			j--;
		}
		else if(flag[i][j]=='u')
			i--;
		else
			j--;
	}
	
	while(!ans.empty())
	{
		cout<<ans.top();
		ans.pop();
	} 
}

int main()
{
    string x = "ABCBDAB";
    string y = "BDCABA";
    vector< vector<int> > dp;
    vector< vector<char> > flag;

    LCS_length(x,y,dp,flag);
    //dp_print_lcs(flag,x,x.size(),y.size());
    stack_print_lcs(flag,x,x.size(),y.size());
    
    return 0;
}