資料倉庫與資料探勘之Apriori演算法例項
阿新 • • 發佈:2018-12-05
最近剛上了資料探勘這門課,老師講了兩個演算法,即Apriori演算法和FP-growth演算法,然後佈置了上機作業,挖掘一個有8萬行的記錄的retail.dat,需要從中找出強規則,即同時滿足最小支援度和最小置信度的規則。
Apriori演算法
在這裡給出一個實現找出所有頻繁模式集的c++程式碼,其中主要使用的儲存結構是二維陣列,有點簡陋,湊合著看看。
另外,這個版本是剛寫出來初始版本,自連線之後沒有修剪步驟,而是直接掃描資料庫,所以效率偏低。
#include<iostream> #include<fstream> #include<algorithm> #include<vector> #include<cctype> using namespace std; void Cin(vector<vector<int> > &arr,vector<int> &a)//讀入二維陣列 { //ifstream fin("test.txt"); ifstream fin("retail.dat"); int num; char p; vector<int> temp_line; while (fin.get(p)) { do { if (p == '\n') { arr.push_back(temp_line); temp_line.clear(); } } while (isspace((int)p) && fin.get(p)); if (!fin) break; fin.putback(p); //將讀取到的資料返回到輸入流中,供下面的fin>>num可以繼續讀取資料 fin >> num; a[num]++; temp_line.push_back(num); } fin.close(); } void ShowData(vector<vector<int> > arr)//輸出全部資料 { cout<<"總行數:"<<arr.size()<<endl; cout << "All the Data: " << endl; for (int i = 0; i < arr.size(); i++) { for(int j = 0; j < arr[i].size(); j++) cout << arr[i][j] << " "; cout << endl; } } int Firitem(vector<int> &v) { //ifstream infile("test.txt"); ifstream infile("retail.dat"); int temp=0; while(infile>>temp){ v.push_back(temp); } sort(v.begin(),v.end()); v.erase(unique(v.begin(), v.end()), v.end()); infile.close(); return v.back(); } void ShowFir(vector<int> a,int Min_sup)//輸出一項集 { int Co=0; cout<<"-------1項集--------"<<endl; for(int i=0;i<a.size();i++) { if(a[i]>=Min_sup) { Co++; cout<<"{ "<<i<<" }: "<<a[i]<<endl; } } cout<<"1項集個數:"<<Co<<endl; } void Com(vector<vector<int> > &Ck,vector<int> a,int Min_sup) { vector<int> t; for(int i=0;i<a.size();i++) { t.clear(); if(a[i]>=Min_sup) { t.push_back(i); } else continue; Ck.push_back(t); } } void Link(vector<vector<int> > &Ck) { vector<int> t1; vector<vector<int> > t2; if(Ck[0].size()==1)//生成二項集 { for(int i=0;i<Ck.size()-1;i++) { for(int j=i+1;j<Ck.size();j++) { t1.push_back(Ck[i][0]); t1.push_back(Ck[j][0]); t1.push_back(0); t2.push_back(t1); t1.clear(); } } } //生成多項集 else { int t; for(int i=0;i<Ck.size()-1;i++) { for(int j=i+1;j<Ck.size();j++) { for(t=0;t<Ck[0].size()-1;t++) { if(Ck[i][t]==Ck[j][t]) { t1.push_back(Ck[i][t]); } else break; } if(t==Ck[0].size()-1) { t1.push_back(Ck[i][Ck[0].size()-1]); t1.push_back(Ck[j][Ck[0].size()-1]); t1.push_back(0); t2.push_back(t1); t1.clear(); } else{ t1.clear(); } } } } Ck=t2; } void TraData(vector<vector<int> > arr,vector<vector<int> > &Ck)//遍歷 { for(int i=0;i<arr.size();i++) { int m=0; while(m<Ck.size()) { int n=0; for(int j=0;j<arr[i].size();j++) { if(Ck[m][n]<arr[i][j]) break; else if(arr[i][j]==Ck[m][n]) { n++; if(n==Ck[m].size()-1) { Ck[m][n]++; break; } } } m++; } } } void ShowItem(vector<vector<int> > Ck,int Min_sup) { int Co=0; cout<<"-------"<<Ck[0].size()-1<<"項集--------"<<endl; for(int i=0;i<Ck.size();i++) { if(Ck[i].back()>=Min_sup) { Co++; cout<<"{ "; for(int j=0;j<Ck[i].size()-1;j++) { cout<<Ck[i][j]<<" "; } cout<<"}: "<<Ck[i].back()<<endl; } } cout<<Ck[0].size()-1<<"項集個數: "<<Co<<endl; } void Delete(vector<vector<int> > &Ck,int Min_sup) { vector<int> t1; vector<vector<int> > t2; for(int i=0;i<Ck.size();i++) { if(Ck[i].back()>=Min_sup) { for(int j=0;j<Ck[i].size()-1;j++) { t1.push_back(Ck[i][j]); } } else continue; t2.push_back(t1); t1.clear(); } Ck=t2; } int main() { vector<vector<int> > arr;//儲存Data集的二維陣列 vector<int> Fir; vector<vector<int> > Ck;//候選項集 int Min_sup; int Firlen; Firlen=Firitem(Fir); vector<int> a(Firlen); cout<<"輸入最小支援度Min_sup:"; cin>>Min_sup; Cin(arr,a); //讀取dat檔案至陣列中 Com(Ck,a,Min_sup); //ShowData(arr);//輸出全部資料 ShowFir(a,Min_sup);//輸出一項集 while(Ck.size()>1) { Link(Ck);//自連線,生成候選項集 TraData(arr,Ck); ShowItem(Ck,Min_sup); Delete(Ck,Min_sup); } cout<<"資料探勘完畢"<<endl; return 0; }
這個版本測試時用的最小支援度是2000,這個支援度比較大,所以輸出結果還是較快的。不過如果最小支援度設為1000以下的話,那麼執行速度就差了很多。
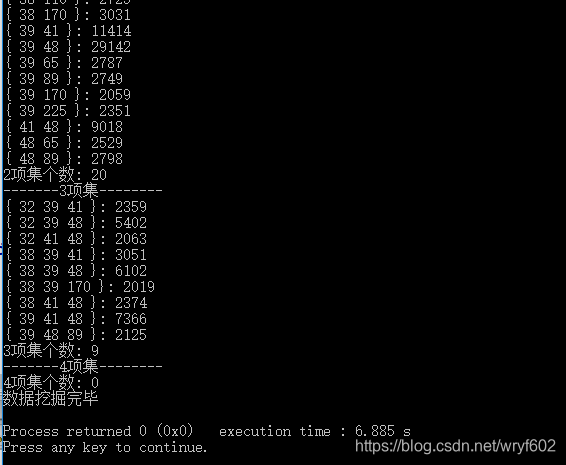
改進之後增加了修剪步驟的演算法執行速度在最小支援度較低時執行速度明顯加快,但是還是耗時較長。
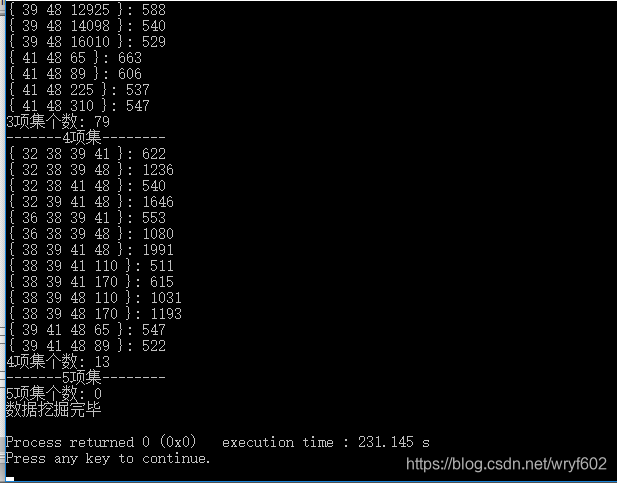
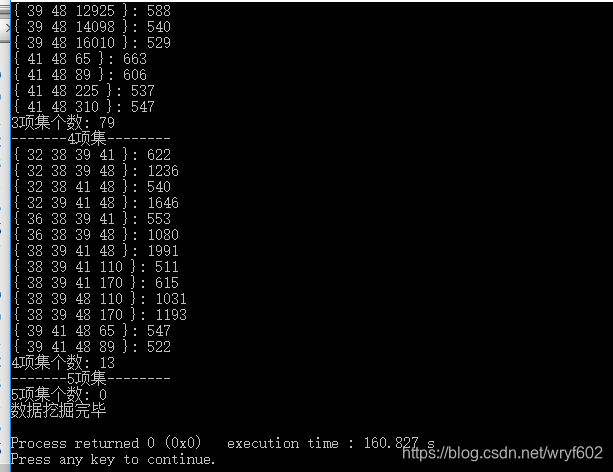
可以看到,在最小支援度在500時,改進後的演算法提升了一分多鐘,因此修剪對於Apriori演算法來說是很重要的一步。
12.02更新
這兩天本來打算補完修剪部分,就去研究一下FP-growth演算法的。結果發現樹的知識還不會,準備先把資料結構的樹部分的OJ題刷完再寫。於是這兩天一直在優化Apriori演算法,終於在參考了韓家偉教授的《資料探勘:概念與技術》一書後,明白了可以用雜湊函式來處理2項集,效率一下子就提上來了。在這裡給出書中的描述。

由於雜湊函式,也就是雜湊函式其實我也不會,百度看了大半天,大概懂了一點,在這裡用二項集的例子嘗試著解釋一下。
在優化前的程式碼中,二項集的處理是每掃描一行資料庫,便需要將二項集中的每一項拿出來比較,假設二項集中有n組項,即一行資料庫就需要掃描n次,效率十分低下。
而對於一項集,則用了計數排序的思想,即在第一次掃描讀取全體資料集時,每讀取一個數temp,便在相應的H[temp]++,如此實現了一項集的快速計數。
如果二項集也能採取類似的方法,那麼執行效率無疑會比現在高出很多。所以雜湊函式就是這麼個東西,我們能夠用一個關鍵字key來表示一組數,這裡用的應該是叫桶雜湊的方法。
首先我們需要創建出一個Hash陣列,其大小由你使用的雜湊演算法決定,然後在掃描生成一項集的同時,對資料集的每一行中的項組成所有的二項集,然後使用雜湊函式hash(x,y)建立散列表,同時進行相應的桶計數。全部掃描完成後,我們便得到了一個存有全體資料集的一個Hash陣列(原諒我只會陣列)。
在我們自連線得到了候選二項集C2後,掃描每一個項{i,j},判斷Hash[hash(i,j)]是否大於你的最小支援度閾值Min_sup,由此可以通過掃描一次候選二項集C2快速的得到一個頻繁二項集L2。
接下來我們看一個簡單的例子
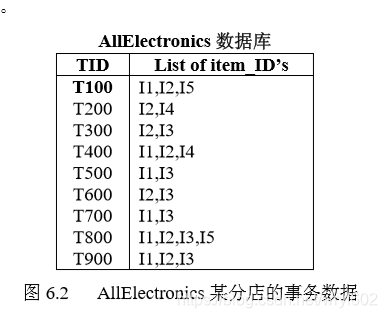
圖6.2中代表一個數據集,我們可以使用函式hash(x,y)=(x10+y)%7建立Hash陣列,顯然其大小size為7。
先看第一行,I1,I2,I5,可以組成三個二項集{I1,I2},{I1,I5},{I2,I5},我們使用函式將其存入Hash陣列中,key=hash(1,2)=(110+2)mod 7=5,H[key]++;hash(1,5)=1,Hash[1]++;hash(2,5)=4,Hash[4]++;即每一個二項集都對應著Hash中的一個key,接下來每一行都可以用該方法存入。
其中{I1,I4},{I3,I5}因為hash(1,4)=hash(3,5)=0,則他們被稱為同義詞,如果我們不進行任何處理的話,在計數中Hash[0]對應的數包含這兩個項。在這裡我們可以使用開放地址法(線性探測法),再雜湊法,鏈地址法解決這種“地址衝突”,由於我也是剛剛快速看完雜湊函式,所以具體的知識都不太瞭解,有興趣的可以自行去查詢相關資料,這裡就不說如何將他們分別存放了。
經過上面這一步,我們在第一次掃描資料集的時候,就同時得到了一個存著資料集中全部二項集的Hash陣列。假設圖6.2中項的最小支援度閾值為2,首先可得到候選二項集為{I1,I2},{I1,I3},{I1,I4},…,{I3,I5},{I4,I5},接著就是掃描全體資料集得出每一個二項集的支援度計數,但是我們已經有了一個存著全部二項集的雜湊陣列,因此我們只需要在Hash找到相應的支援度就可以了。如{I1,I2}的支援度為Hash[hash(1,2)],如果該數值大於2,即存入頻繁二項集L2中。
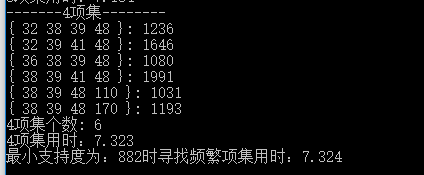
改進後的演算法1%支援度掃描時間由20多秒減少到了7秒,進步了不少。不過存在的問題還是比較多,各個地方差缺補漏的,越寫越亂,可讀性極差。
