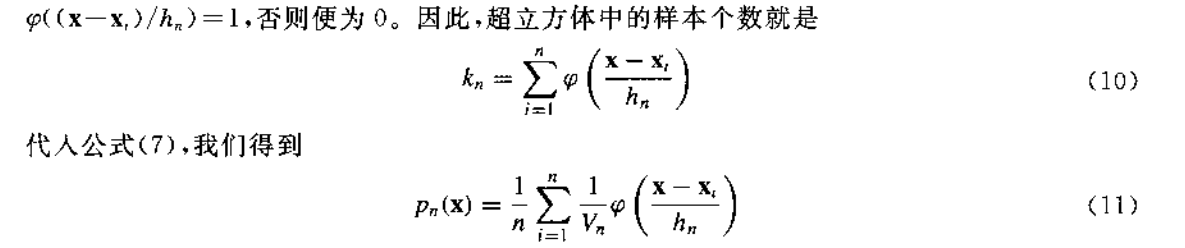
## 1.簡介 Parzen窗估計屬於**非引數估計**。所謂非引數估計是指，已知樣本所屬的類別，但未知總體概率密度函式的形式，要求我們直接推斷概率密度函式本身。 > 對於不瞭解的可以看一下https://zhuanlan.zhihu.com/p/88562356 **下面僅對《模式分類》（第二版）的內容進行簡單探討和程式碼實現** ## 2.窗函式   我們不去過多探討什麼是窗函式，只需簡單理解這種估計的思想即可。 假設一種情況，你正在屋裡看模式分類，結果天降正義掉下來一盆乒乓球，掉的哪裡都是，你覺得這是天意，如果很多乒乓球都掉在了一個位置，那麼那個位置下一次必掉屠龍寶刀，你想通過估計屋子裡乒乓球密度，找出這個位置，那麼如何估計呢？ 假設你的屋裡正好鋪了地磚，每塊地磚的大小都相同。你此時靈機一動，我只需要**統計每塊地磚上的乒乓球個數**，有最多乒乓球的地磚就是屠龍寶刀的位置。 這似乎聽起來很簡單，的確，就是這麼簡單。我們回頭看一下公式（9），**其中$ \varphi \left( \mathbf{u} \right)$其實就是判斷某個乒乓球是否在某個地磚上的一個函式**，這裡的$\mathbf{u}$是 **乒乓球相對地磚中心的位置**。 這裡$\mathbf{u}$是$\mathbf{x}-\mathbf{x}_{\mathbf{i}}$，$\mathbf{x_i}$是地磚中心的位置，而$\mathbf{x}$是乒乓球的位置。  那麼公式（9）就顯而易見了，如上圖所示，你屋子裡一塊地磚的邊長為${h}$，紅色乒乓球在地磚內，藍色乒乓球沒有在地磚內，判斷的條件顯然就是向量$\mathbf{x}-\mathbf{x}_{\mathbf{i}}$的每個元素是否小於$\frac{1}{2}h$，我們可以直接對$\mathbf{x}-\mathbf{x}_{\mathbf{i}}$乘以$\frac{1}{h}$，這樣我們的窗函式就可以寫成公式（9）的樣子，只需要看引數$\mathbf{u}=\frac{\mathbf{x}-\mathbf{x}_{\mathbf{i}}}{h}$的每個元素是否小於$\frac{1}{2}$即可。 然後呢？ 到這裡工作差不多就結束了，我們看哪塊地磚上乒乓球最多就行。 對於某塊中心在$\mathbf{x_i}$的地磚，地磚上的乒乓球個數$k$就是公式（10） 有了每塊地磚上的乒乓球個數，概率密度的估計就很簡單了。 $$ p\left( \mathbf{x} \right) =\frac{k}{nV}\quad V=h^d $$ 一共$n$個球，有$k$個球落在某個地磚上，地磚的面積為$V=h^2$（別忘了地磚是二維空間），那$p(\mathbf{x})$就出來了。 到這裡，公式（11）也不需要我說什麼了吧 - 這裡所寫的窗函式表示超立方體，而不是超球體，判斷條件也不是點到中心的距離小於2/h，而是點座標的每個元素都小於2/h。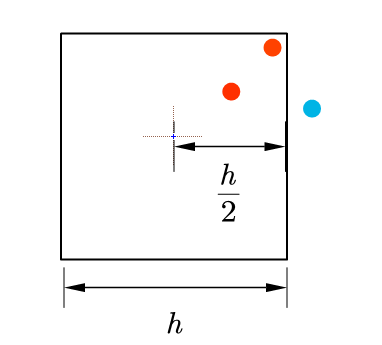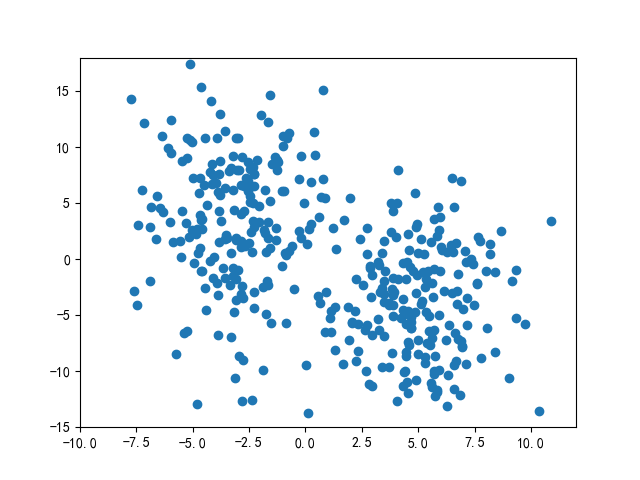 ## 3.大地磚和小地磚 假設**400**個乒乓球在你房間的大致分為兩堆，它們的分佈可近似為 $$ \left( x_1\sim N\left(-3,4 \right) ,y_1\sim N\left(4,36 \right) \right) \\ \left( x_2\sim N\left( 5, 4 \right),y_2\sim N\left(-4,25 \right) \right) \\ $$ 乒乓球位置如下圖所示  你為了更好的估計乒乓球的密度，用魔法不斷更改著地磚的大小，如下圖所示，地磚的邊長分別為8、5、2，黃點為座標為(1,4)的地磚所包含的乒乓球，紅點為地磚中心。我們可以看到隨著$h$的不斷變化，每個地磚所包含的乒乓球數量是不同的。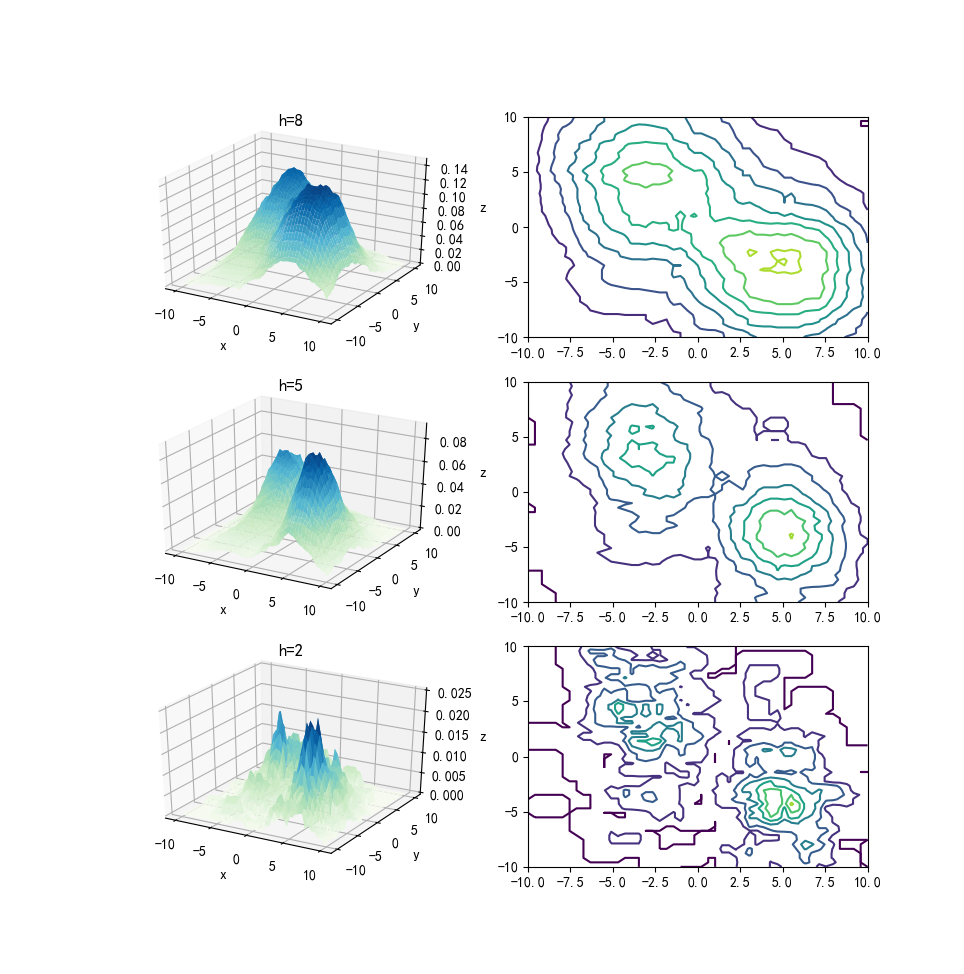  下面我們可以看到三種不同大小的地磚估計出來的概率密度，如下圖所示：  所以說。。咳咳，這裡直接放原話。  ## 4.一盆球和無限球 假設我們不再是400個球，我們有。。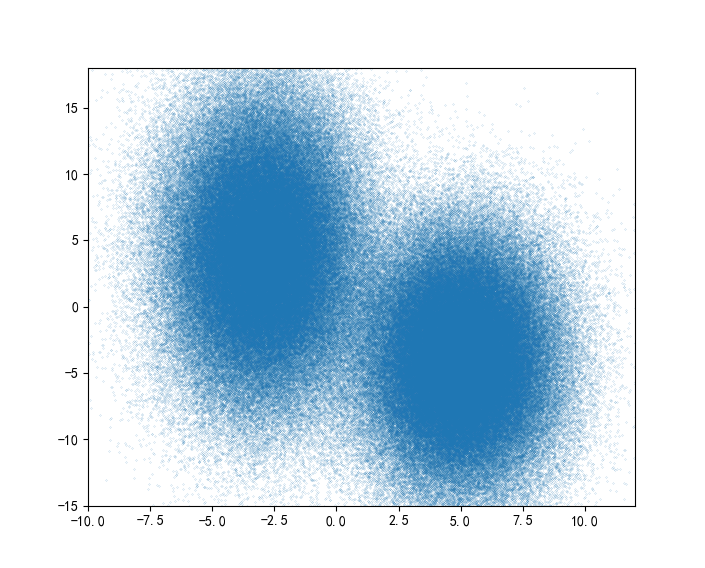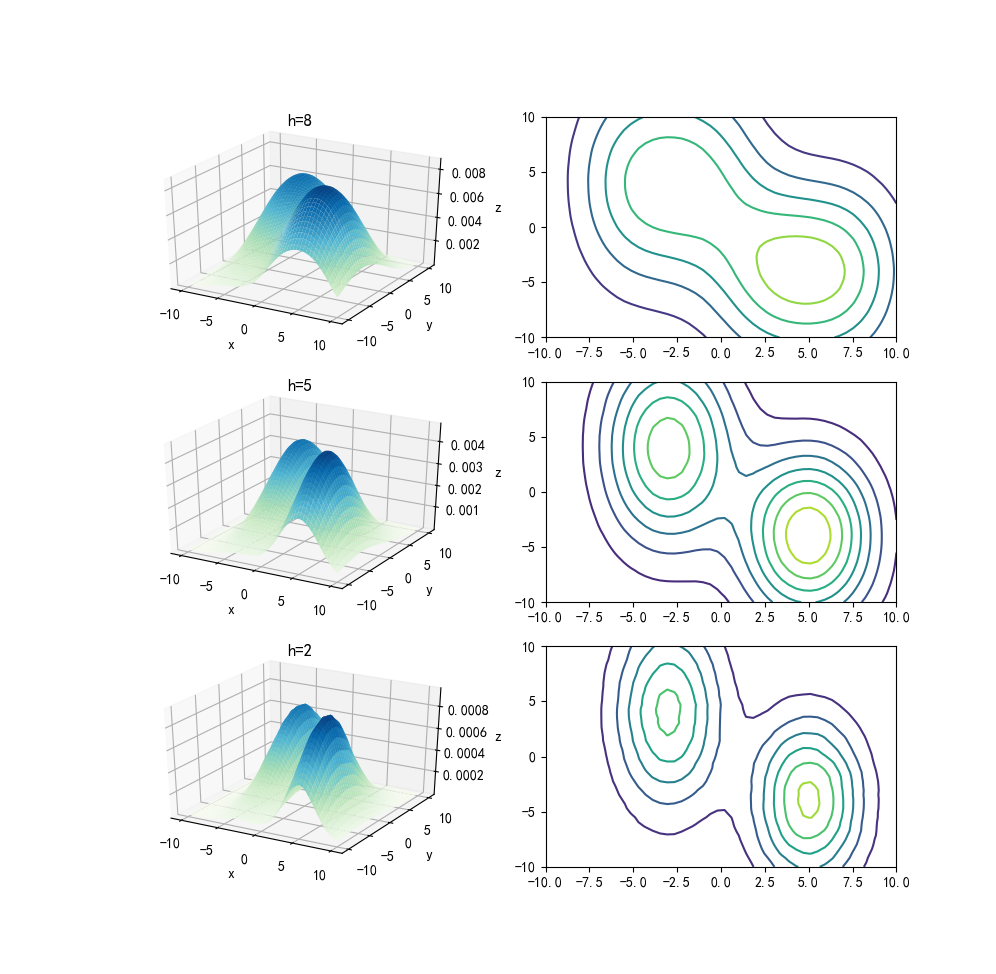400000個球，怎麼樣，真·天降正義，首先乒乓球的分佈是這樣的：  我們再次用邊長為8、5、2的地磚對乒乓球進行概率密度估計，如下圖所示  說白了其實都差不多，顯而易見的事情，這裡再放出一個原話 **當n趨近於無窮大時，$p_n(x)$將收斂於光滑的$p(x)$曲線** ## 程式碼附錄 jupyter格式 環境：python 3.7 ```python #%% # 生成資料 import matplotlib.pyplot as plt %matplotlib auto import numpy as np n = 200000 datax = np.hstack([np.random.randn(n)*2-3, np.random.randn(n)*2+5]) datay = np.hstack([np.random.randn(n)* 6+4, np.random.randn (n)*5-4]) xi = np.array([1,4]) xv,yv = datax,datay pos = np.vstack([datax,datay]) ``` ```python #%% # 散點圖 plt.figure(1) plot_pos = 131 for h in [8,5,2]: plt.subplot(plot_pos) plot_pos += 1 Vn = h ** 2 u = (pos - xi.reshape(-1,1))/h # u = (x - xi)/h ix,iy = pos[:,(abs(u)<=0.5).all(axis=0)] plt.xlim([-10,12]) plt.ylim([-15,18]) plt.title("h="+str(h)) plt.scatter(xv,yv,s=0.01) plt.scatter(ix,iy) plt.scatter(xi[0],xi[1],c='r') plt.show() ``` ```python #%% # 三維概率密度圖 和 等高線圖 def px(x): u = (pos - x.reshape(-1,1))/ h # u = (x - xi)/h ix,iy = pos[:,(abs(u)<=0.5).all(axis=0)] k = len(ix) return k / (Vn * n) w = 50 gx = gy = np.linspace(-10,10,w) gxv,gyv = np.meshgrid(gx,gy) fgxv = gxv.ravel() fgyv = gyv.ravel() plt.figure(3) plot_pos = 321 for i in [8,5,2]: h = i fpx = np.array([px(x) for x in np.vstack([fgxv,fgyv]).T]) fpx = fpx.reshape(w,w) ax = plt.subplot(plot_pos,projection='3d') plot_pos += 1 ax.plot_surface(gxv,gyv,fpx,cmap='GnBu') ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('h='+str(h)) ax = plt.subplot(plot_pos) plot_pos += 1 ax.contour(gxv,gyv,fpx) plt.sho