視訊編解碼學習詳解:變換,量化與熵編碼
阿新 • • 發佈:2019-02-15
第6章 變換編碼
1. 變換編碼
- 變換編碼的目的
- 去除空間訊號的相關性
- 將空間訊號的能力集中到頻域的一小部分低頻係數上
- 能量小的係數可通過量化去除,而不會嚴重影響重構影象的質量
- 塊變換和全域性變換
- 塊變換:離散餘弦變換(Discrete Cosine Transform,DCT),4x4,8x8,16x16
- 全域性變換:小波變換(Wavelet)
- 變換的能量集中特性
- DCT編碼
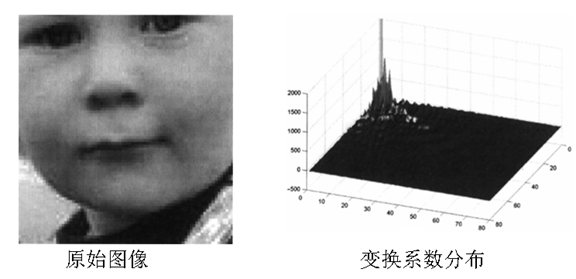
2. 變換型別
- K-L變換
- 傅立葉變換
- 餘弦變換
- 小波變換
3. KL變換
- 最優變換
- 基函式根據具體影象而確定
- 沒有快速演算法
- 實際中很少使用
- 複雜度極高



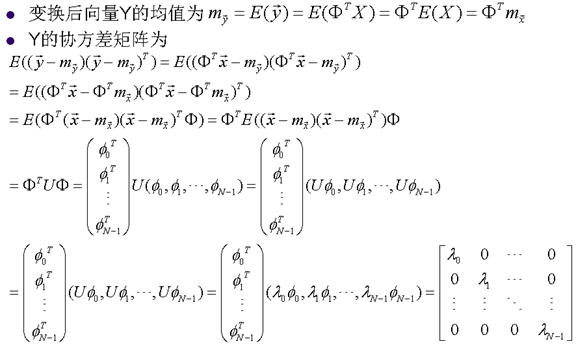

- K-L變換非常複雜度很高,不實用
- 需要計算協方差矩陣U
- 需要計算特徵向量
- 需要傳送 到解碼器
4. 離散傅立葉變換

5. 離散傅立葉變換性質


6. 離散餘弦變換
- 比K-L變換,傅立葉變換的複雜度更低
- 變換效能僅次於K-L變換
- 有快速演算法可以加快變換速度
- 可以用整數變換進一步降低複雜度
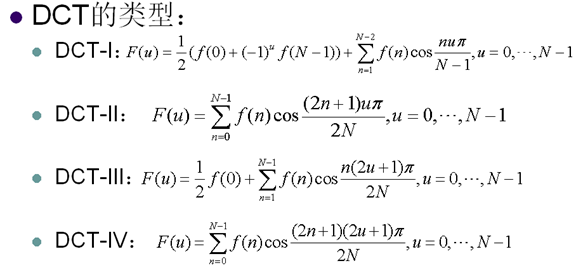



7. DCT與DFT的關係

8. 離散餘弦變換的重要性質
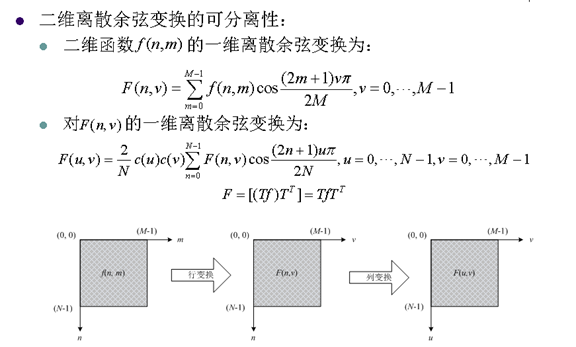

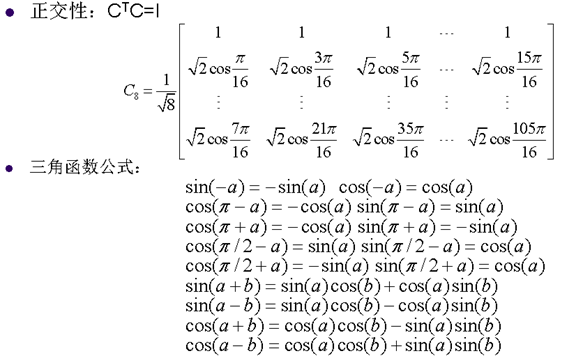
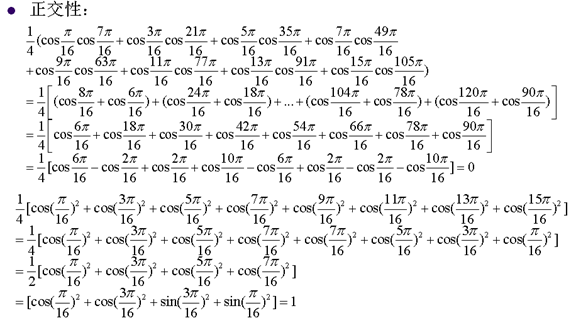
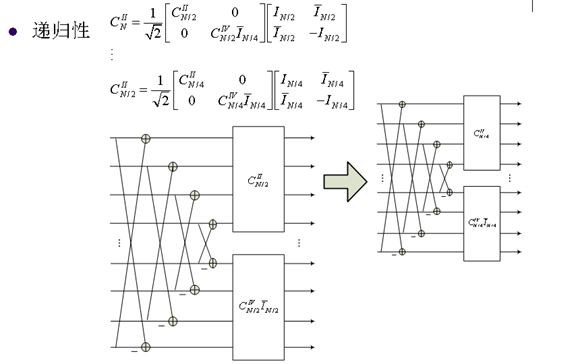
9. 快速DCT變換

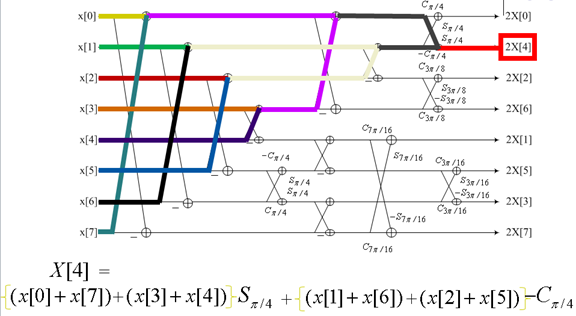
下圖是一個動態展示:

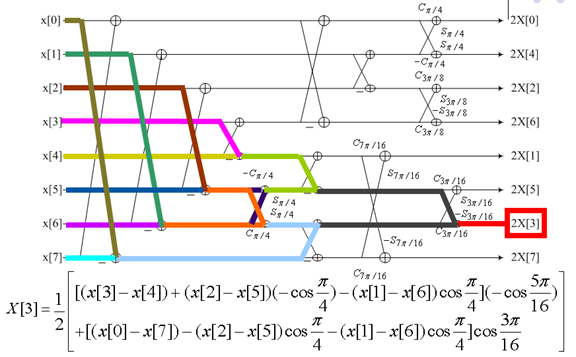
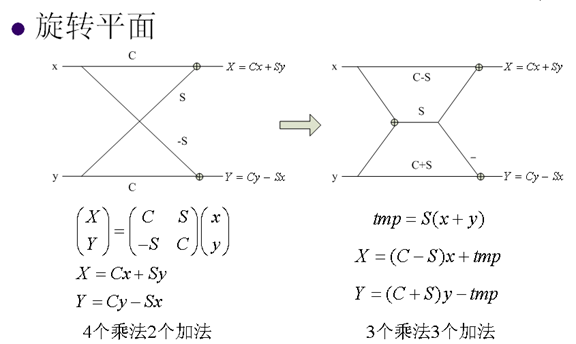
10. 整數離散餘弦變換
- 離散餘弦變換為浮點操作
- 需要64位精度
- 浮點計算複雜度高
- 變換精度高
- 整數變換:離散餘弦變換的整數近似
- 需要更少的位寬
- 整數計算複雜度低
- 好的整數變換的變換精度接近浮點變換
- 浮點近似方法

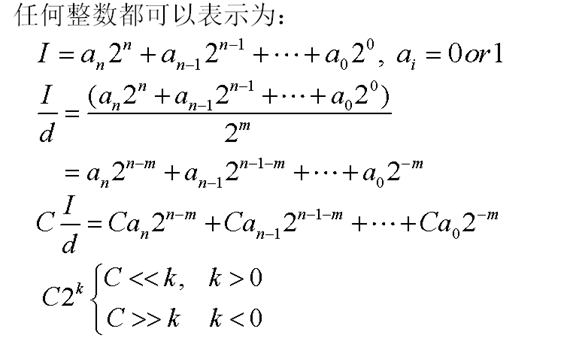

11. H.264的4x4整數變換



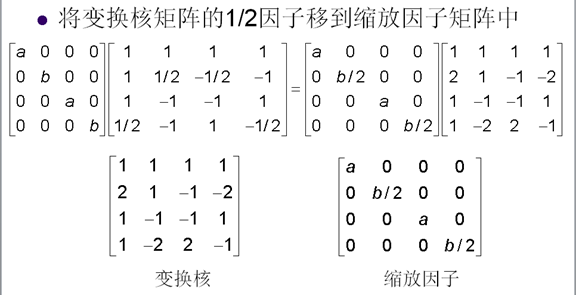
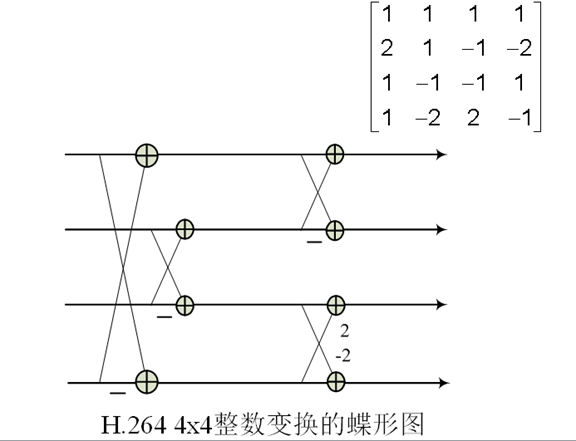



12. 小波變換
- 新的變換方法
- 避免由於塊編碼帶來的塊效應
- 更適合視訊空間可分級編碼
第7章 量化
1. 量化Quantization
- 用更小的集合表示更大的集合的過程
- 對訊號源的有限近似
- 有損過程
- 應用
- A/D轉換
- 壓縮
- 量化方法
- 標量(Scalar)量化
- 向量(Vector)量化
2. 量化的基本思想
- 對映一個輸入間隔到一個整數
- 減少信源編碼的bit
- 一般情況重構值與輸入值不同
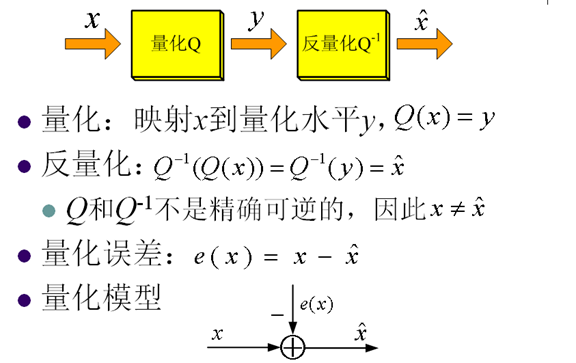
3. 量化模型
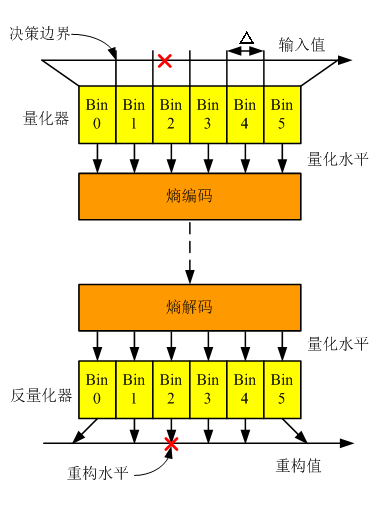
4. 量化的率失真優化
- 量化器設計問題
- 量化水平的個數,即Bin的個數
- 決策邊界:Bin的邊界
- 重構水平
- 量化器設計是對率失真的優化
- 為了減少位元速率的大小,需要減少Bin的個數
- Bin的個數減少導致重構的誤差增大,失真也就隨著增大

5. 失真測量

6. 量化器設計
- 量化器設計的兩個方面
- 給定量化水平數目M,找到決策邊界xi和重構水平使MSE最小
- 給定失真限制D,找到量化水平數目M,決策邊界xi和重構水平yi使MSE<=D

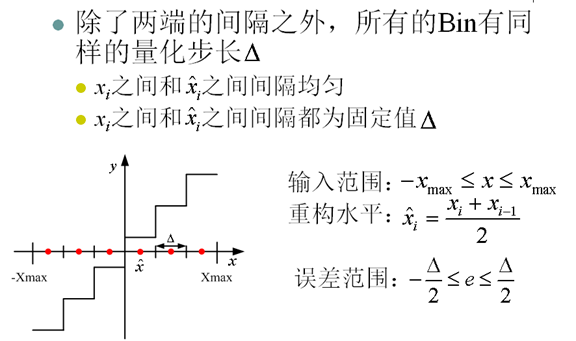
7. 均勻量化(Uniform Quantization)
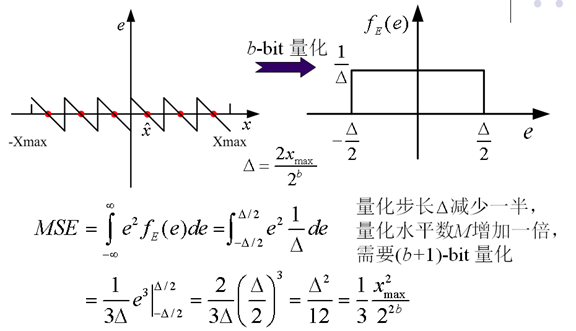
8. 量化與峰值信噪比


9. 中升量化器(Midrise Quantizer)

10. 中平量化器(Midtread Quantizer)
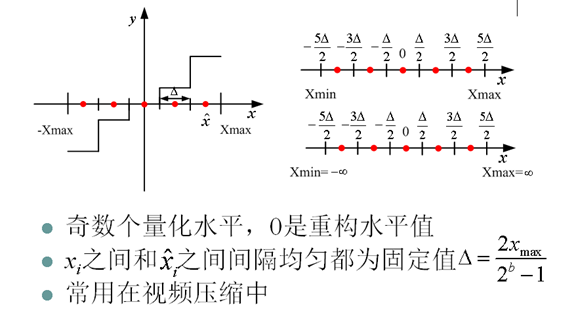
11. 死區量化器(Deadzone Quantizer)
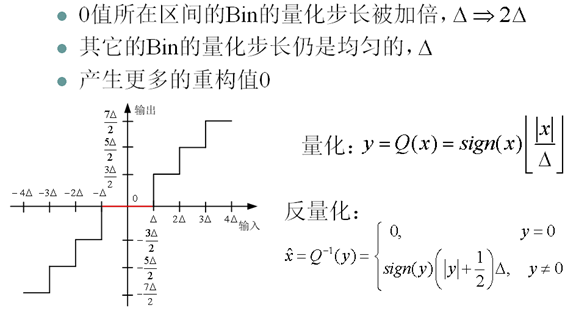
12.非均勻量化(Non-uniform Quantization)
- 如果信源不是均勻分佈的,採用均勻量化不是最優的
- 對於非均勻量化,為了減少MSE,當概率密度函式fX(x)高時,使Bin的量化步長減小,當概率密度函式fX(x)低時, 使Bin的量化步長增加。

13. 最優的標量量化
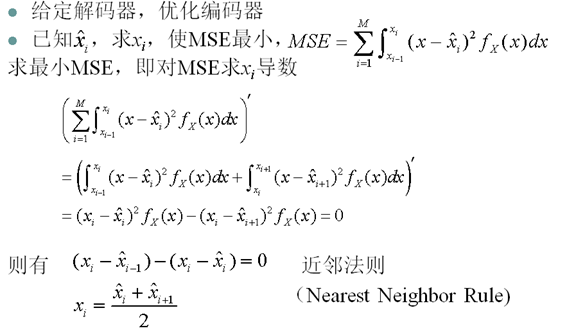

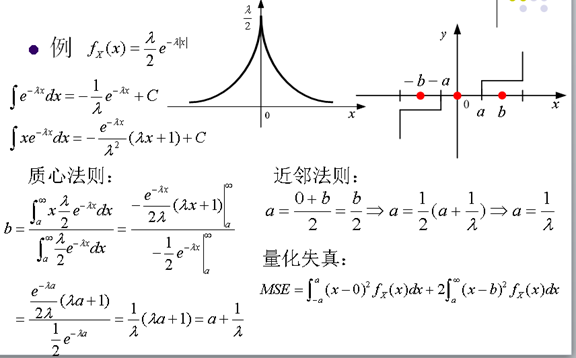
14. 量化編碼
- 定長編碼量化水平
- 使用等長的碼字編碼每個量化水平,碼字長為:
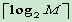
- 使用等長的碼字編碼每個量化水平,碼字長為:
- 熵編碼量化水平
- 根據量化水平的概率分佈情況,用變長的碼字編碼每個量化水平
- 平均碼字長
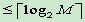
- 比定長編碼量化水平效率高
- 廣泛應用在影象和視訊編碼中
15. 向量量化
- 標量量化:對資料一個一個的進行量化,稱為標量量化。
- 向量量化:將資料分組,每組K個數據構成K維向量,再以向量為處理單元進行量化。
- 向量量化是標量量化的多維擴充套件
- 標量量化是向量量化的特殊情況
- 向量量化工作過程
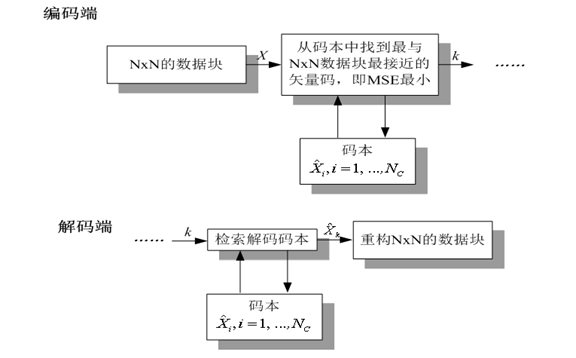

- 二維向量量化
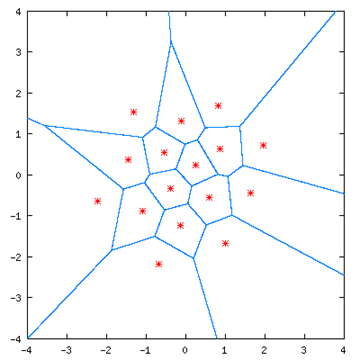
- 向量量化優點
- 只傳碼字的下標,編碼效率高
- 在相同位元速率下,比標量量化失真小
- 在相同失真下,比標量量化位元速率低
- 向量量化缺點:複雜度隨著維數的增加呈指數增加
第8章 熵編碼
1. 熵編碼
- 熵(Entropy):信源的平均資訊量,更精確的描述為表示信源所有符號包含資訊的平均位元數
- 信源編碼要儘可能的減少信源的冗餘,使之接近熵
- 用更少的位元傳遞更多的信源資訊
- 熵編碼:資料壓縮中根據信源訊息的概率模型使訊息的熵最小化
- 無失真壓縮
- 變長編碼
2. 熵
- 資訊量:
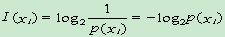
單位:位元
- 熵:
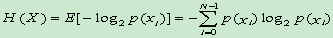
單位:位元/符號


3. 定長編碼

4. 變長編碼
- 變長編碼:用不同的位元數表示每一個符號
- 為頻繁發生的符號分配短碼字
- 為很少發生的符號分配長碼字
- 比定長編碼有更高的效率
- 常用的變長編碼
- Huffman編碼
- 算術編碼
5. Huffman編碼
- 字首碼:任何碼字不是其它碼字的字首
- 如果011為一個有效碼字,則0,1,01,11必不是有效碼字
- 不會引起解碼歧義
- Huffman:
- 二叉樹
- 樹節點:表示符號或符號組合
- 分支:兩個分支一個表示"0",另一個表示"1"
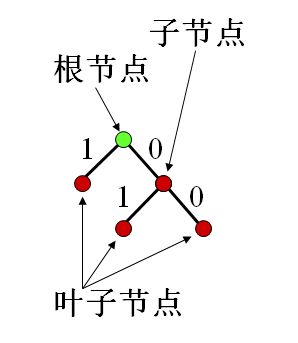
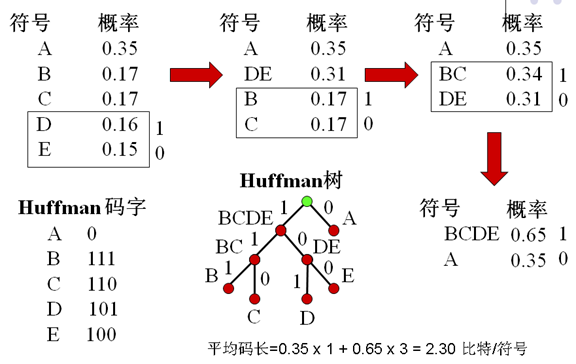
- Huffman的不唯一性
- 每次分支有兩種選擇:0,1

- 相同的概率產生不同的組合
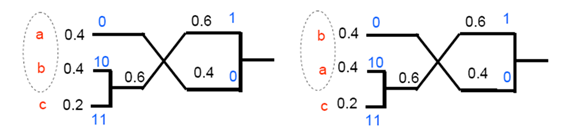
- 每次分支有兩種選擇:0,1
- 缺點:
- 資料的概率變化難於實時統計
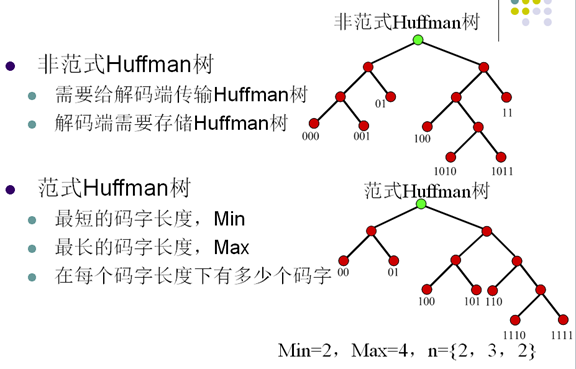
- Huffman樹需要編碼傳輸給解碼器
- 只有在p(xi)=1/2ki 時是最優編碼
- 最小碼字長度為1位元/符號
- 如果有二值信源,其兩個符號的概率相差很大
- 例如:p(1)=0.0625,p(0)=0.9375則H=0.3373位元/符號,Huffman編碼平均碼長=1位元/符號
- 兩個符號聯合編碼有更高效率
6. 擴充套件Huffman編碼
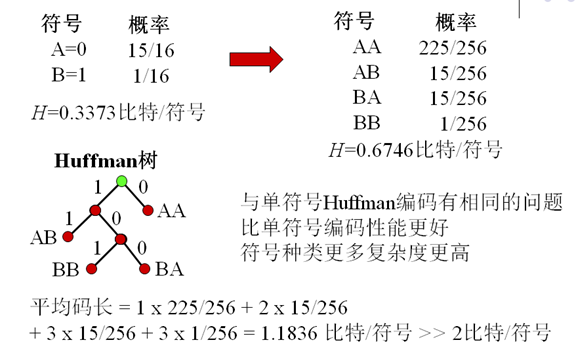
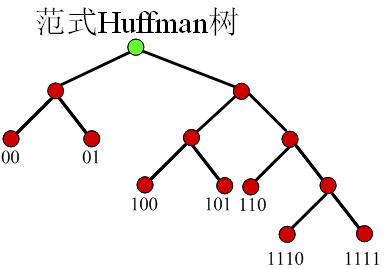
7. 正規化Huffman編碼
- 正規化Huffman樹的建立規則
- 節點左支設為0,右支設為1
- 樹的深度從左至右增加
- 每個符號被放在最先滿足的葉子節點
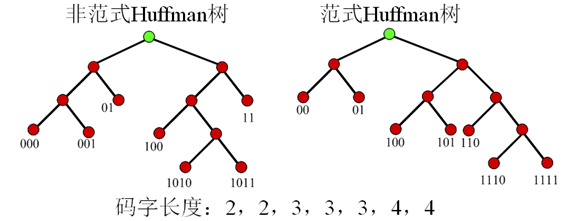
- 特性
- 第一個碼字是一串0
- 相同長度的碼字的值是連續的
- 如果所有的碼字通過在低位補0的方式,使所有碼字的長度相同則有 0000<0100<1000<1010<1100<1110<1111
- 從碼字長度n到n+1有如下關係
- C(n+1,1)=(C(n,last)+1)<<1
- 從碼字長度n到n+2有如下關係
- C(n+2,1)=(C(n,last)+1)<<2
8. 一元碼
- 編碼一個非負整數n為n個1和一個0
- 不需要儲存碼錶
- 可以用Huffman樹表示
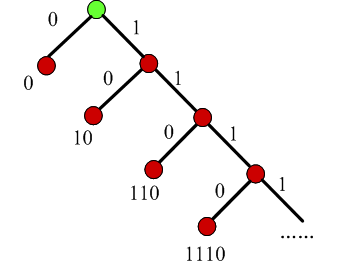
- 碼長增長太快:n=100,碼長101

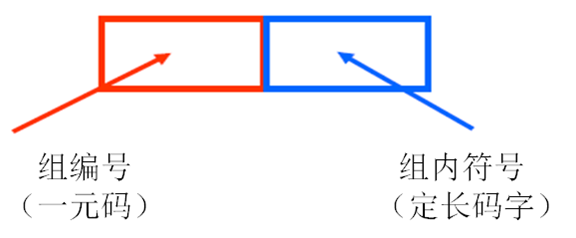
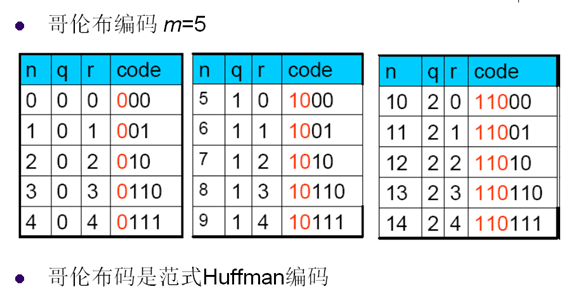
9. 哥倫布編碼
- 將信源符號等分成幾組,每組有相應的編號
- 編號小的分配碼字短,編號大分配碼字長
- 同組的符號有等長的碼字,比一元碼的碼字長度增長慢

- 碼字分配

10. 指數哥倫布編碼
- 哥倫布碼對信源符號的分組大小相同
- 指數哥倫布碼對信源符號的分組大小按照指數增長
- 指數哥倫布碼依然是一元碼加定長碼的形式
- 指數哥倫布碼的指數k=0,1,2,…



11. CAVLC( Context-Based Adaptive Variable Length Code)
- 當前塊的係數分佈和其鄰塊的係數分佈情況相關
- NX為塊X的非零係數個數,當前塊C的第一個係數的編碼碼錶由NC決定, NC=( NA+ NB )/2
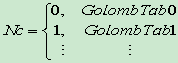
- NX為塊X的非零係數個數,當前塊C的第一個係數的編碼碼錶由NC決定, NC=( NA+ NB )/2
- 當前待編碼係數和前面編碼係數有相關性
- 當前塊C的其它係數的編碼碼錶由前一個係數的幅值決定cofN-1=>GolombTab_x,用GolombTab_x編碼cofN

12. 算術編碼
- 資訊量=>符號編碼位元數
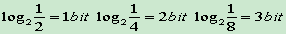
- Huffman編碼為每個符號分配一個碼字,這說明Huffman編碼的壓縮上限是1位元/符號
- 算術編碼若干個符號可編碼成1bit
- 算術編碼是把信源表示為實數軸上[0,1]區間,信源中每個符號都用來縮短這個區間
- 輸出[0,1]區間的一個實數表示一串編碼符號
- 比Huffman編碼更有效
- 編碼思想
- 編碼器用熵編碼演算法編碼一串符號產生一個[0,1]區間的實數,將實數的一個二進位制表示傳給解碼器
- 解碼器用熵解碼演算法解碼得到一串符號
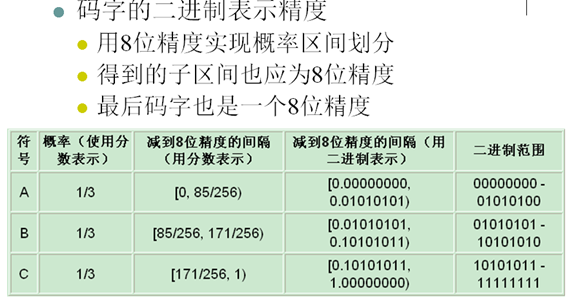
- 小數的二進位制表示
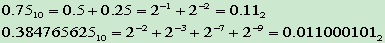
- 信源符號概率分佈
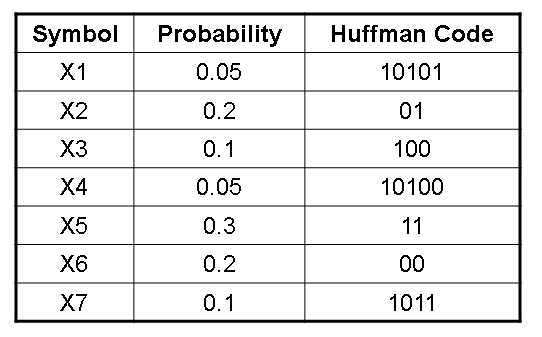
- 字串:X2 X2 X3 X3 X6 X5 X7
- Huffman編碼,01 01 100 100 00 11 1011,18bit
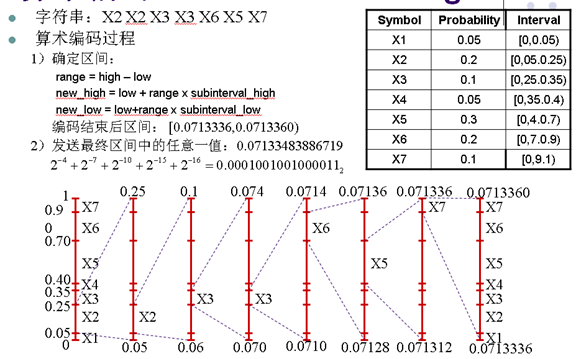
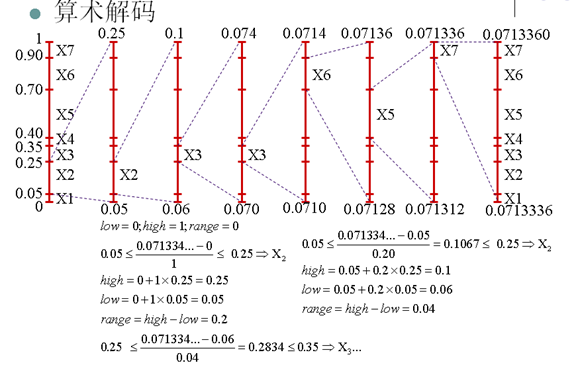
- 算術編碼更接近熵
- 有限精度算術編碼是次優(Near-optimal)編碼,傳送整數位元給解碼端
- 算術編碼到最後一個字元編碼結束才輸出碼字
- 編碼複雜度也比較高
13. 二值算術編碼

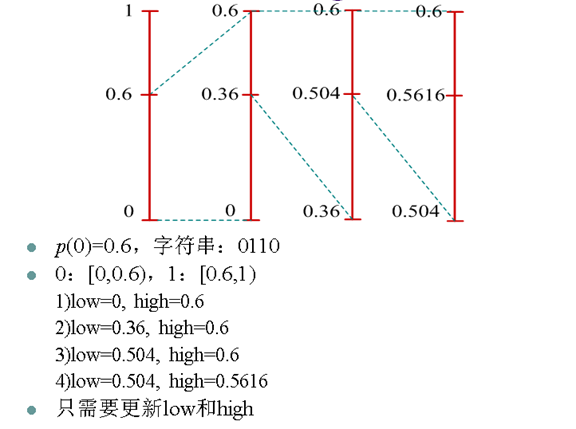

13. 自適應二值算術編碼
- 由於信源0和1出現的概率是在不斷變化的,因此0和1的概率區間也應該不斷改變
- 自適應二值算術編碼每編碼一個0或1都重新統計0和1的概率並重新劃分[0,1)區間
- 編解碼端的概率統計模型一致,能夠得到同樣的[0,1)區間劃分


14. CABAC(Context-Based Adaptive Binary Arithmetic Coding)
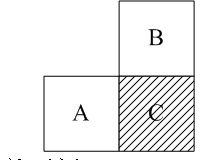
- 當前塊的語法元素概率分佈和其鄰塊的語法元素概率分佈情況相關
- 當前塊C的鄰塊A和B的語法元素SA與SB可以為編碼C塊的語法元素SC選擇概率模型
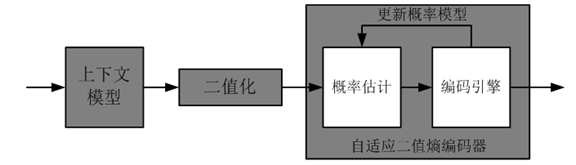
- 二值化
- 將語法元素值轉換成二進位制值串
- 概率模型更新
- 根據已經編碼的位元,重新估計二進位制值串的概率並更新概率模型,用新的概率模型編碼下一個位元
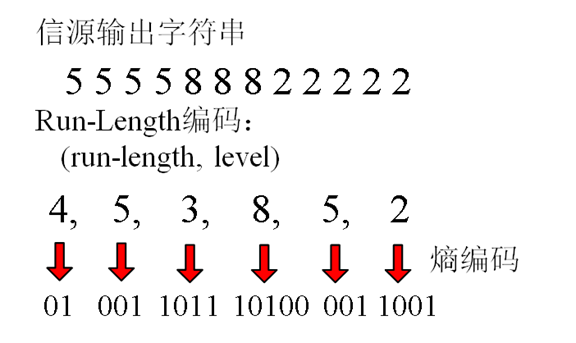
15. Run Length 編碼
- 利用信源字元的重複性來編碼的技術
- 對有很長,很多重複字元的信源編碼非常有效
- 重複字元稱為run,重複的字元個數稱為run length
- Run-length編碼能夠和其它熵編碼一起來壓縮資料

16. 字典編碼
- 字典編碼:根據信源符號(訊息)的組合特點,建立包含各種符號組合的字典,編碼這些符號組合的索引
- LZ78=>Winzip
- LZW=> GIF
- 適合一般意義上的資料壓縮,去除資料的統計冗餘
17. LZW
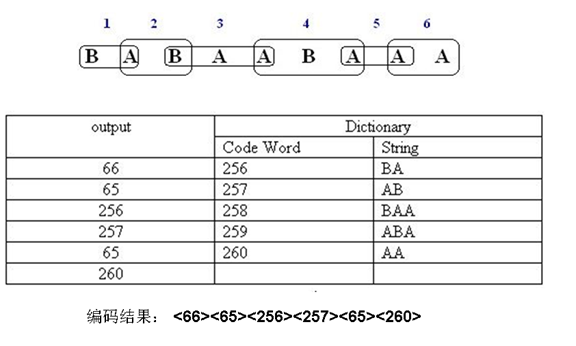
- 將信源輸出的字串中,每個第一次出現的字元或者字串用索引來表示,並將字元或字串對應的索引編碼到碼流中
- 解碼端根據從碼流中解碼的字元,線上的建立和編碼器完全一樣的字典,並恢復出信源輸出的字串
- 適用於字串中有大量的子字串多次重複出現,重複次數越多,壓縮效果越好
- 單個符號被分配為0-255之間的值
- 初始碼錶,使其包含值為0-255的256個符號,值大於255的符號為空
- 編碼器將根據編碼的符號情況確定字元組合為從 256 到 4095 之間的值
- 編碼時,編碼器識別新的字元組合,並將他們增加到碼錶中
- 編碼器用碼錶中的符號組合所對應的值編碼
- 解壓時LZW解碼器能夠產生和編碼器完全一樣的碼錶
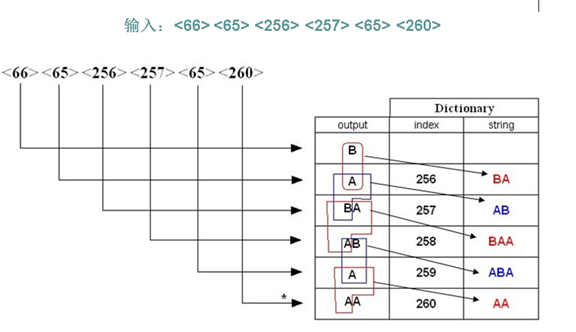
- 和編碼器一樣先初始化所有的單字元,將0-255之間的值分配給它們
- 除了解碼第一個字元外,解碼其它字元時都要更新碼錶
- 通過讀碼字並根據碼錶中的值將它們解碼為對應的字元或字元組合
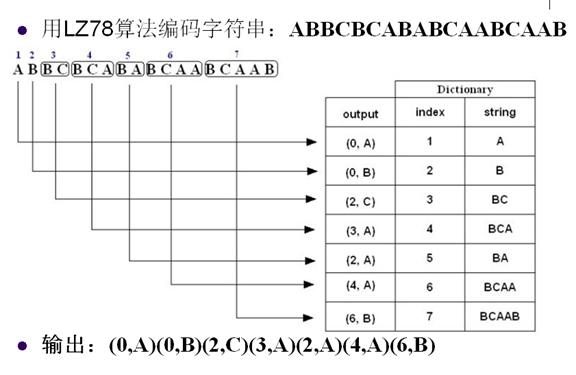
18. LZ78

參考資料:
