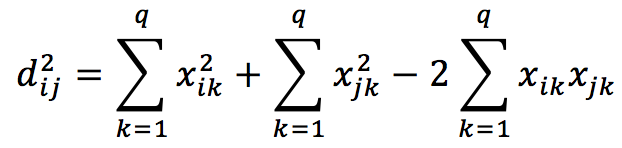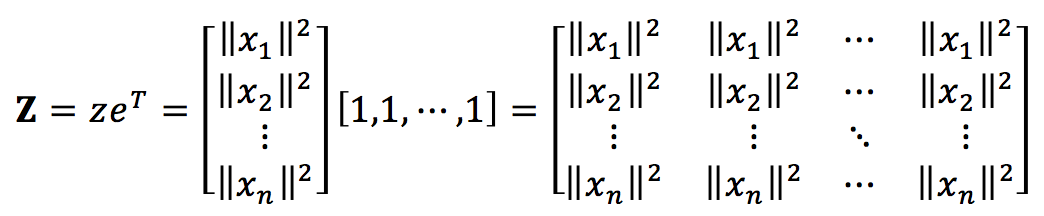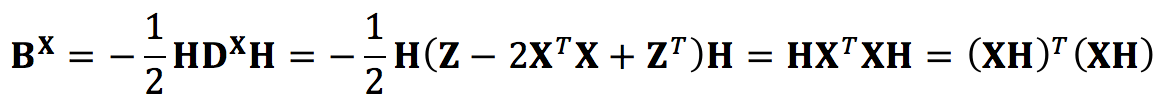流形學習（Manifold Learning）是機器學習中一大類演算法的統稱，而MDS就是其中非常經典的一種方法。多維標度法（Multidimensional Scaling）是一種在低維空間展示“距離”資料結構的多元資料分析技術，簡稱MDS。

多維標度法解決的問題是：當n個物件（object）中各對物件之間的相似性（或距離）給定時，確定這些物件在低維空間中的表示，並使其儘可能與原先的相似性（或距離）“大體匹配”，使得由降維所引起的任何變形達到最小。多維空間中排列的每一個點代表一個物件，因此點間的距離與物件間的相似性高度相關。也就是說，兩個相似的物件由多維空間中兩個距離相近的點表示，而兩個不相似的物件則由多維空間兩個距離較遠的點表示。多維空間通常為二維或三維的歐氏空間，但也可以是非歐氏三維以上空間。

多維標度法內容豐富、方法較多。按相似性（距離）資料測量尺度的不同MDS可分為：度量MDS和非度量MDS。當利用原始相似性（距離）的實際數值為間隔尺度和比率尺度時稱為度量MDS（metric MDS），本文將以最常用的Classic MDS為例來演示MDS的技術與應用。

首先我們提出這樣一個問題，下表是美國十個城市之間的飛行距離，我們如何在平面座標上據此標出這10城市之間的相對位置，使之儘可能接近表中的距離資料呢？

首先我們在R中把csv格式儲存的資料檔案讀入，如下所示：

> data.csv = read.csv("/Users/fzuo/Desktop/data.csv", header = T, row.names = 1)
> data.csv
     ATL  ORD  DEN  HOU  LAX  MIA  JFK  SFO  SEA  IAD
ATL    0  587 1212  701 1936  604  748 2139 2182  543
ORD  587    0  920  940 1745 1188  713 1858 1737  597
DEN 1212  920    0  879  831 1726 1631  949 1021 1494
HOU  701  940  879    0 1374  968 1420 1645 1891 1220
LAX 1936 1745  831 1374    0 2339 2451  347  959 2300
MIA  604 1188 1726  968 2339    0 1092 2594 2734  923
JFK  748  713 1631 1420 2451 1092    0 2571 2408  205
SFO 2139 1858  949 1645  347 2594 2571    0  678 2442
SEA 2182 1737 1021 1891  959 2734 2408  678    0 2329
IAD  543  597 1494 1220 2300  923  205 2442 2329    0
 

在解釋具體原理之前，我們先來呼叫R中的內建函式來實現上述資料的MDS，並展示一下效果，此處需要用到的函式是cmdscale()。

> citys<-cmdscale(data.csv, k=2)

然後用圖形化的方式來展示一下得到的資料點分佈圖

> cities.names = rownames(data.csv)
> plot(citys[,1],citys[,2],type='n')
> text(citys[,1],citys[,2],cities.names,cex=.7)

執行上述程式碼，結果如下圖所示：

與實際的地圖對照，東西方向反了，應該是左東右西，所以可以把上面的繪圖程式碼稍加修改，則有

> plot(-citys[,1],citys[,2],type='n', ylim=c(-600,600)) 
> text(-citys[,1],citys[,2],cities.names,cex=.7)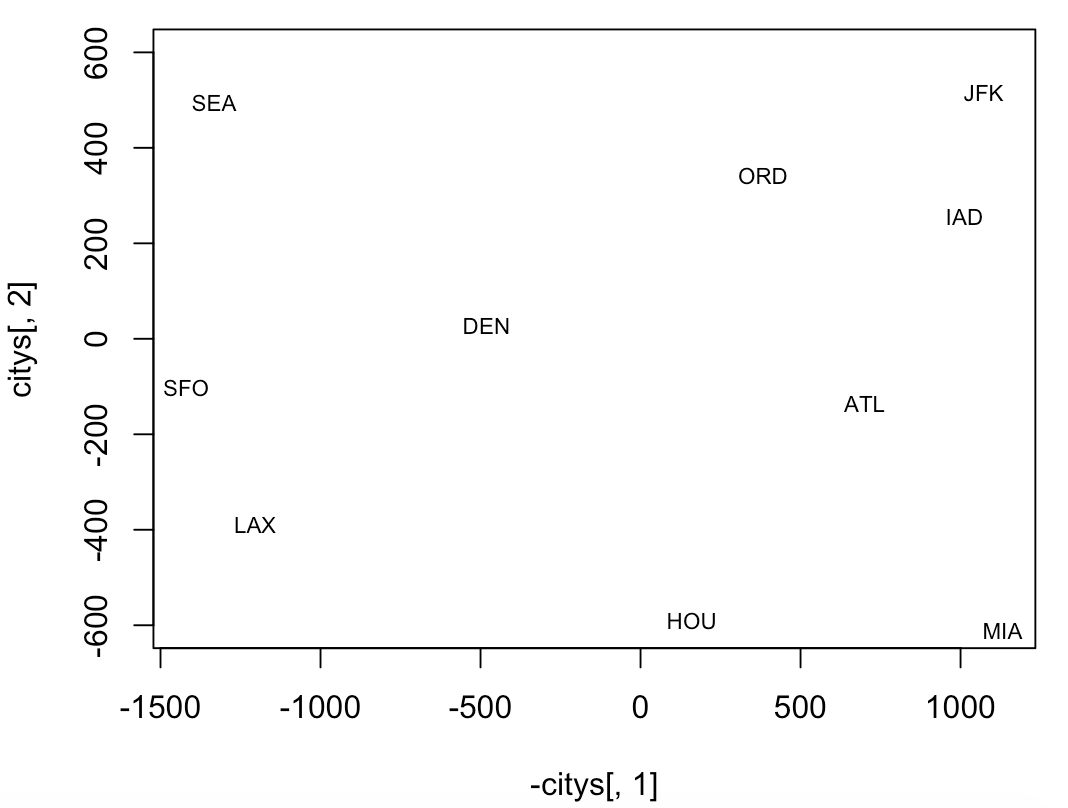

執行上述程式碼，結果如下圖所示：

還可以把上圖同實際的美國地圖做個對照，易見各個城市在圖中的位置與實際情況匹配得相當好。

如此神奇的MDS，它背後的原理到底是什麼呢，或者它到底是如何實現的呢？下面我們就來抽絲剝繭。

假設X={x₁, x₂, ..., x_n}是一個n×q的矩陣，n為樣本數，q是原始的維度，其中每個x_i是矩陣X的一列，x_i∈R^q。我們並不知道x_i在空間中的具體位置，也就是說對於每個x_i，其座標(x_i1, x_i2, ... , x_iq) 都是未知的。我們所知道的僅僅是the pair-wise Euclidean distances for X，我們用一個矩陣D^X來表示。因此，對於D^X中的每一個元素，可以寫成

或者可以寫成

對於矩陣D^X，則有

其中，

這裡的z為

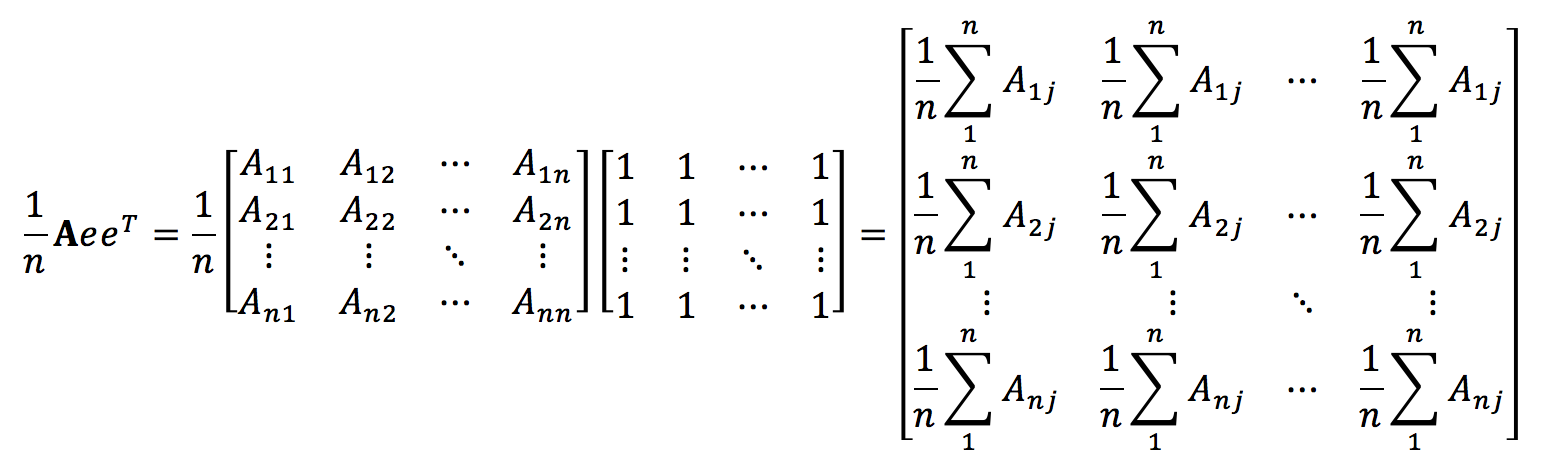
現在讓我們來做平移，從而使得矩陣D^X中的點具有zero mean，注意平移操作並不會改變X中各個點的相對關係。為了便於理解，我們先來考察一下Aee^T/n和ee^TA/n的意義，其中A是一個n×n的方陣。

不難發現Aee^T/n中第i行的每個元素都是A中第i行的均值，類似的，我們還可以知道，ee^TA/n中第i列的每個元素都是A中第i列的均值。因此，我可以定義centering matrix H如下

所以D^XH的作用就是從D^X中的每個元素裡減去列均值，HD^XH的作用就是在此基礎上再從DX每個元素裡又減去了行均值，因此centering matrix的作用就是把元素分佈的中心平移到座標原點，從而實現zero mean的效果。更重要的是，Let D be a distance matrix, one can transform it to an inner product matrix （Kernel Matrix） by K=-HDH/2, 即