也許是史上最不良心的低階計算幾何講解和習題集??
-3.在此宣告:
筆者極端厭惡計算幾何,以至於直到今天之前都只打過幾個計算幾何的模板~~~~~
不過鑑於今年是18年,所以感覺SD很有可能考計算幾何(18年是什麼理由啊喂)
於是滾過來整理計算幾何的資料了......
-2.可能會用到的資料:
《計算幾何——演算法與應用》
Mark·Overmars 著 鄧俊輝 譯
《計算幾何導論》
[美] F·P·普霍帕拉塔 M·I·沙莫斯 著
——好像是一些沒什麼用的東西呢
《演算法導論——第33章》
[美]Tomas H.Cormen Charles E.Leiserson Ronald L.Rivest Clifford Stein 著
——聽說是可以提升文章逼格的東西呢
本文會盡量(大概吧)把上述文獻中對OI有用的部分扒拉出來
《藍書》
劉汝佳 著
《紫書》
劉汝佳 著
某些大佬的blog——%%%%%%%%%%%%%%%%%%%%%%%%%%%
-1.可能會用到的OJ:
BZOJ——儘管他很爆炸
POJ——儘管全是英文
HDU——我好像沒怎麼用過
luogu——很良心的OJ吧,大概......
LOJ——幾乎沒用過,應該也用不到吧
UOJ——不用搜索引擎就能翻出需要的題——如果需要的題真的湊巧在這個OJ裡的話
0.於是正文開始:
(廢話真多)
計算幾何最重要的是(拼命調)關注點和向量
1.幾何的準備工作(可以直接略過而和後文沒什麼聯絡的工作):
1.1.一般定義和記法以及一些可有可無且並不全面的說明:
計算幾何的研究物件往往是基於歐幾里得空間的點集的,
因為,當我們存在一個座標系時
一個點可以有一個座標,於是與原點構成了向量——實際上,在許多大佬的計算幾何模板中都將點和向量巨集定義為一個東西,如劉汝佳的《藍書》
兩個點可以構成一個線段或者直線,直線可以定義半平面交
多個點可以構成多邊形,或者凸包——事實上凸包和半平面交存在著諸多相似性
多邊形可以各種剖分
而且,相比於用其他元素描述上述內容而言,座標系中的點是更加適用於計算機語言的,因為一個點表示成有序數對之後,與任何數對(pair)無異
當然以上胡扯也可以扯到擴充套件到更高的維度上去
於是約定有如下不常用的記法:
$E^d$表示d維歐幾里得空間,(在下文中,d一般大於等於2且不超過3,——由於筆者水平而有的限制)
在d維歐幾里得空間中,有如下基本物件:
1.1.1.點、向量——
一個d元組$(x_1,x_2,...,x_d)$,他可以表示一個點P,也可以表示一個起點為$E^d$的原點O,終點為點P的一個有d個分量的向量
1.1.2.線、平面——
給定$E^d$中兩個不同的點$P_1$,$P_1$的線性組合
$$aP_1+(1-a)P_2(a∈R)$$
可以表示$E^d$中的一條直線(如果把P看做向量的話,上式是高中數學中常見的向量基本定理推論)
給定$E^d$中三個不同的點$P_1$,$P_2$,$P_3$的線性組合
$$aP_1+bP_2+(1-a-b)P_3$$
可以表示$E^d$中的一個平面
類似的上面關於線面的定義也可以推廣的更高的維度而成為一種叫做線性簇的東西
(沒有用)
線段——
給上文中的直線表示式中加一個對a的範圍限制,可以得到一條線段
如,加入限制(0≤a≤1)可以得到一個以$P_1$,$P_2$位端點的線段,可以表示為$\overline{P_1P_2}$或$\overline{P_2P_1}$
1.1.3.凸集——
若$E^d$中的點集D中的任何兩點$P_1,P_2$,$\overline{P_1P_2}$中的所有點屬於D,則稱D是$E^d$中的一個凸集
凸集的交是凸集
直線中的任意線段是凸集
平面內的任意凸多邊形是凸集
空間中的任意凸多面體是凸集
關於更高維的凸集的相關性質,可移步《線性規劃》——反正筆者看了一點就直接棄療了的說
凸殼與凸包——
$E^d$中點集S的凸包是$E^d$中包含S的最小凸集,
凸殼是凸包的邊界
1.1.4. 多邊形——
在$E^2$中多邊形定義為線段的一個有限集合使得每個端點恰為兩條邊所共有,且沒有邊的子集具有該性質(多邊形僅指這一個邊界部分)
注意:
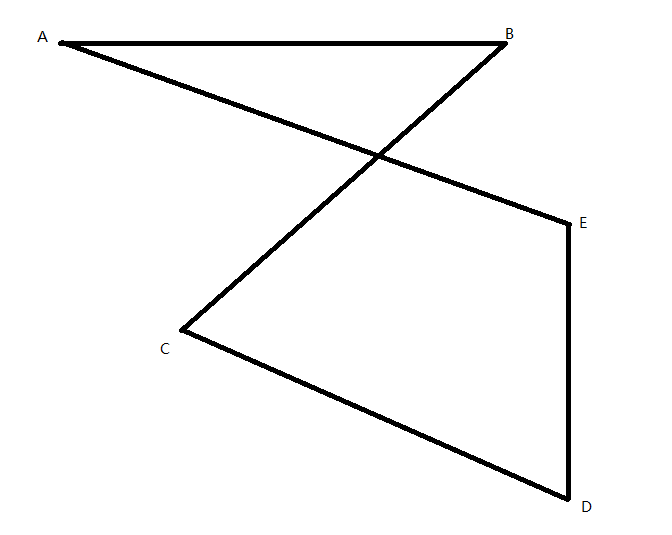
是多邊形
而
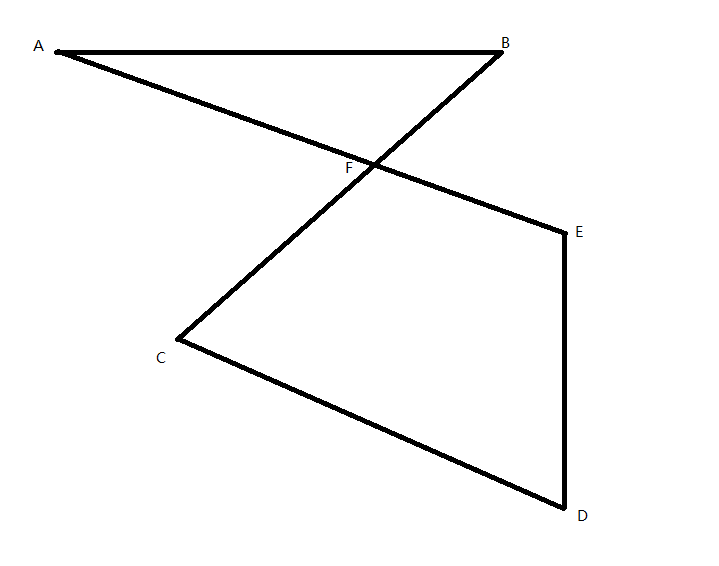
不是
多邊形的其他內容沒有什麼值得強調的
簡單多邊形——
若不相鄰的邊無公共點,則多邊形是簡單的
如上上圖中的多邊形就不是簡單的
簡單多邊形把平面劃成兩個不相交的區域
稱為為多邊形的內部和外部
凸多邊形與星形多邊形——
若簡單多邊形P的內部是個凸集,則此簡單多邊形是凸多邊形
若存在點z在簡單多邊形P的內部或邊上,滿足對於P的所有點p,線段$\overline{zp}$屬於P的內部或屬於P邊,則說明多邊形P是星形的
(因此每個凸多邊形都是星形的)
然而:
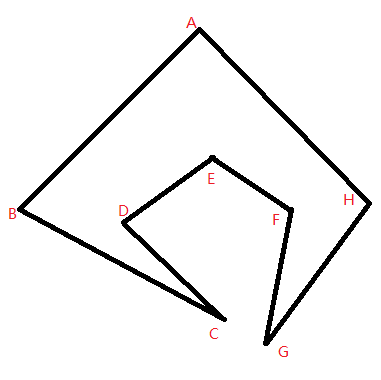
如上圖就不是星形多邊形
在星形多邊形P中,所有z構成的集合為P的核(he?hu?)容易證明,核是一個凸集
(可以用凸集的定義來證)
2.二維幾何——點與向量與線段的性質:
這一部分將在$E^2$內
以向量的計算為基礎
討論點與線段的關係,線段與線段的關係
將介紹如何定義一個點,如何定義一個向量
如何實現向量的基本計算
如何用點和向量表示直線、線段,進而用點和向量實現對直線線段的操作
這大概是計算幾何中最簡單的一部分,將會貼上一些模板
2.1.二維向量的基本運算:
向量的基本運算作為處理計算幾何點線的基礎出現
2.1.1.由於一些眾所周知的原因,首先定義精度:

const double eps=1e-10; int dcmp(double x){ if(fabs(x)<eps)return 0; else return x<0?-1:1; }//精度eps&dcmp
2.1.2.定義點與向量:

struct Point{ double x,y; Point(double x=0,double y=0):x(x),y(y){ }; };//定義點 typedef Point Vector;//定義向量Point&Vector
2.1.3.定義向量加:

Vector operator + (Point A,Point B){ return Vector(A.x+B.x,A.y+B.y); }//定義向量加符合三角形定則Vector +
2.1.4.定義向量減:

Vector operator - (Point A,Point B){ return Vector(A.x-B.x,A.y-B.y); }//定義向量減符合三角形定則Vector -
2.1.5.定義向量數乘:

Vector operator * (Vector A,double p){ return Vector(A.x*p,A.y*p); }//定義向量數乘 Vector operator * (double p,Vector A){ return Vector(A.x*p,A.y*p); }//定義向量數乘Vector *
(直接分別定義左右乘了,並不會其他更高階的方式)
2.1.6.定義向量數除:

Vector operator / (Vector A,double p){ return Vector(A.x/p,A.y/p); }//定義向量數除Vector /
2.1.7.定義向量相等(用到了精度):

bool operator == (const Point& a,const Point& b){ return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0; }//定義向量相等為完全相同Vector ==
2.1.8.向量極角:
即從x軸正半軸旋轉到該向量方向所需的弧度,(單位:弧度)

double Polar_Angle (Vector A){ return atan2(A.y,A.x); }//計算向量極角Polar Angel
2.1.9.向量旋轉:
將向量p(x,y)繞起點逆時針旋轉弧度a,得到$p'(xcosa-ysina,xsina+ycosa)$
2.1.10.二維向量的點積:
如果你已經學習了《數學必修》的內容,則你應該對點積十分了解

double Dot(Vector A,Vector B){ return A.x*B.x+A.y*B.y; }//計算向量點積Dot
座標對應相乘再相加,點積的結果是一個實數,可認為是模長乘夾角cos
2.1.11.二維向量的叉積:
如果你有一定的物理或數學水平,則你應該明白二維向量的叉積結果應該是三維空間中的一個垂直於這個兩個向量向量,方向按照右手法則判定
然而因為使用範圍的限制,這裡對叉積的定義十分淺顯:
考慮向量$p_1(x_1,y_1),p_2(x_1,y_1)$的叉積定義為把兩個向量起點移動到同一處後得到的三點圍成的三角形的有向面積的兩倍
或者定義為下述矩陣的行列式的值:
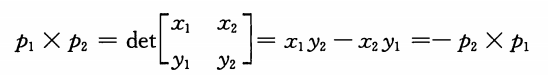
若其為正,則相對於原點來說$p_1$位於$p_2$的順時針方向,若其為0,則兩向量共線

double Cross(Vector A,Vector B){ return A.x*B.y-A.y*B.x; }//計算向量叉積Cross
交叉相乘再相減,可看做模長乘夾角sin
注意:叉積沒有交換律
2.1.12.由點積叉積拓展來:
於是有了一個簡單的基於叉積的計算三點圍成三角形面積的演算法:

double Area(Point A,Point B,Point C){ return fabs(Cross(B-A,C-A)/2); }//計算abc三點三角形的數值面積Area
於是有了一個簡單的基於點積的計算向量長的演算法:

double Length(Vector A){ return sqrt(Dot(A,A)); }//計算向量模長Length
於是有了一個簡單的基於點積的計算向量夾角的演算法:

double Angle(Vector A,Vector B){ return acos(Dot(A,B)/Lenth(A)/Lenth(B)); }//計算向量夾角(有序的)Angle
2.2.通過向量來判定線段之間的關係:
線段取其兩端點,定義為無序的一對點
而直線則取其中一點和直線的方向向量,定義為一個點和一個向量的二元組
(也可以看做兩個向量,也可以看做兩個點)
這一部分的存在應用價值(嗎?)
2.2.1.確定連續線段的偏轉方向:
討論在點$p_1$處,連續線段$\overline{p_0p_1}$,$\overline{p_1p_2}$的旋轉方向,即判定給定角$∠p_0p_1p_2$的轉向,而我們可以通過計算$\overrightarrow{p_0p_1}$$\overrightarrow{p_0p_2}$叉積結果,來避免直接對角的計算,若其為正,則說明後一條線段向逆時針偏折;若其為負,則說明後一條線段向順時針偏折;若其為零,則兩條線段共線

int Direction(Vector p0,Vector p1,Vector p2){ double num=Cross(Vector(p1-p0),Vector(p2-p0)); return dcmp(num); }//判斷p0->p1,p1->p2的偏轉方向,1為逆時針,-1為順時針,0為共線Direction
2.2.2.判定直線交點:
在之前,我們定義的線性組合$a\vec{A}+(1-a)\vec{B}(a∈R)$為直線,
簡單地,我們定義直線的方向向量為$\vec{v}=\vec{A}-\vec{B}$,
化簡,於是有了$B+a\vec{v}$
方向向量界定了直線的方向,向量B的終點B界定了直線在笛卡爾座標系中的位置,使用規範的符號,於是有了引數方程:
$$P+t\vec v$$
其中t的不同取值代表了直線上的不同點
於是,設$l_1:P+t\vec v $,$l_2:Q+t\vec w $,聯立兩引數方程可解得交點在$l_1$的引數$t_1$,在$l_2$的引數$t_2$,若設$\vec u =P-Q$則有關於$t_1,t_2$的公式如下:
$$t_1={cross(\vec w,\vec u)\over cross(\vec v,\vec w)},t_2={cross(\vec v,\vec u)\over cross(\vec v,\vec w)}$$

Point GetLineIntersection(Point P,Vector v,Point Q,Vector w){ Vector u=P-Q; double t=Cross(w,u)/Cross(v,w); return P+v*t; }//用引數方程求取直線交點——如果他存在的話Get Line Intersection
實際上,運用簡單的高中解析幾何知識就足以解決此問題了吧
2.3.通過向量處理點與直線、點與線段的關係:
這一部分有應用的價值(嗎)
2.3.1.點到直線的距離:
直接叉積求解即可

double DistanceToLine(Point P,Point A,Point B){ return abs(Cross(B-A,P-A)/Length(B-A)); }//P到直線AB的距離Distance To Line
2.3.2.點到線段的距離:
需要令人十分不愉快的分類討論:
設P在直線AB上的投影點為Q,
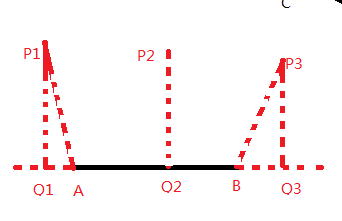 \
\
1:Q線上段外,據A較近,需要求解PA的長
2:Q線上段AB上,直接使用點到直線距離
3:Q線上段外,據B較近,需要求解PB的長
判定可以通過點積來實現

double DistanceToSigment(Point P,Point A,Point B){ if(A==B)return Length(P-A); if(dcmp(Dot(P-A,B-A))<0) return Length(P-A); if(dcmp(Dot(P-B,A-B))<0) return Length(P-B); return DistanceToLine(P,A,B); }//P到線段AB的距離Distance To Sigment
習題:
POJ P2318
POJ P1269
UVa11796(UVA的小題目挺有意思的,適合心情好的時候)
3.二維幾何——簡單多邊形與圓與二維幾何對點集和平面的處理:
於是我們很愉快地從對點線的討論正式轉入圖形了
這一部分將討論對多邊形問題的解決,
進而研究凸包凸殼半平面交等基於點線物件
然後將給出圓的定義
3.1.簡單多邊形部分:
多邊形是在二維幾何中經常研究的圖形,
多邊形取其所有頂點和他們的逆時針連線順序而定義為一個有序點集
具體的定義已經在本文的第一部分提及,所以不作贅述,
接下來將介紹簡單多邊形圍成有向面積的求法
點與多邊形關係的判定
3.1.1.簡單多邊形的有向面積:
考慮凸多邊形的有向面積?
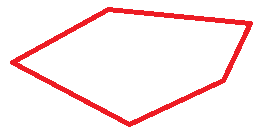
可以從一個點出發把凸多邊形劃成n-2個三角形,求面積再求和
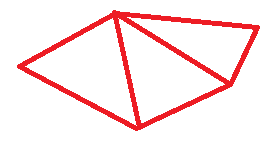
這個方法對非凸的簡單多邊形同樣適用——因為三角形面積的有向性使得在多邊形外部的部分被抵消掉
具體的做法是,把多邊形的n個頂點按照連線順序從0到n-1編號,從$P_0$依次向$P_1$到$P_{n-1}$連向量$\vec{v}$,計算$\sum_{i=1}^{n-2}{cross(\vec{v_i},\vec{v_{i+1}})\over 2}$

(深色部分正負相抵)

double PolygonArea(Point *p,int n){ double area=0; int i; for(i=1;i<n-1;i++) area+=Cross(p[i]-p[0],p[i+1]-p[0]); return area/2; }//計算多邊形的有向面積,也許在結果上加個||更有用些??Polygon Area
3.1.2.點在多邊形內部的判定:
一下演算法適用於所有點按連線順序逆時針排列的簡單多邊形
如何判定p點是否在多邊形Poly內部呢
粗略地想,從點p向右引一條平行於x軸的射線
由於射線無限長而多邊形內部範圍有限,
所以射線無限遠處的盡頭所在的區域一定是多邊形外部
由於多邊形每一條邊兩側一定分屬多邊形的內外
所以從射線遠離p的一側向p走,
第一次經過一條邊將到達多邊形內
第二次經過一條邊將到達多邊形外
以此類推經過——
若該射線奇數次穿過邊,則點p在多邊形內,反之亦然
一些細節,
如果射線的某段與某條邊重合,則這條邊不應計入次數
如果射線穿過某端點,應該如何判定呢
比較好的方法是定義邊的方向為從編號小的點到編號大的點
這樣以後再定義
從下往上穿過射線的邊包含起點不包含終點
從上往下穿過射線的邊包含終點不包含起點
這樣若穿過的端點所在的兩邊同向則只被計算一次
若穿過的端點所在的邊反向則要麼一次都不計算,要麼直接算兩次


int isPointInPolygon(Point p,Point poly[],int n){ int wn=0,i,k,d1,d2; for(i=0;i<n;i++){ if(!dcmp(DistanceToSigment(p,poly[i],poly[(i+1)%n]))) return -1;//在邊界上 k=dcmp(Cross(poly[(i+1)%n]-poly[i],p-poly[i])); d1=dcmp(poly[i].y-p.y); d2=dcmp(poly[(i+1)%n].y-p.y); if(k>0&&d1<=0&&d2>0)wn++;//點在左,下上穿 if(k<0&&d2<=0&&d1>0)wn++;//點在右,上下穿 } return wn&1;//T:內部;F:外部 }//判定點是否在多邊形內部is Point In Polygon
3.2.凸多邊形、對踵點和旋轉卡殼演算法:
凸多邊形的對踵點是凸多邊形上存在的不只一對的點對,
每對對踵點$(p_1,p_1)$滿足都是凸多邊形的頂點且存在過$p_1$的某條凸多邊形的切線與某條過$p_2$的凸多邊形切線平行
對踵點個數不超過(3n/2)
旋轉卡殼演算法是一種通過處理凸多邊形的對踵點來解決一系列凸多邊形問題的演算法
筆者將旋轉卡殼演算法從多邊形中剝離出來(主要是因為他內容比較多)
這裡給出用旋轉卡殼列舉所有對踵點的方法:
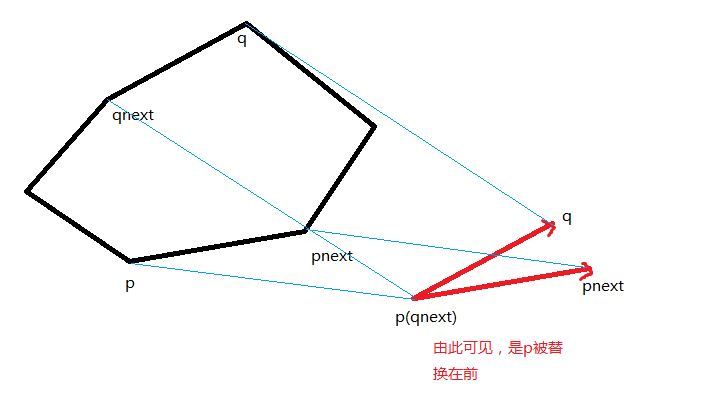
先找到y最小的點$p=p_{ymin}$,和y最大的點$q=p_{ymax}$,他們是一對對踵點,
從這對對踵點分別向逆時針方向引出平行於x軸的射線,
按相同的角速度逆時針轉動這對射線,直到其中一條穿過多邊形的下一端點$p_{next}$,{p_{next}}將代替他所在的射線的原端點成為射線的新端點,並和另一射線的端點構成新的對踵點,
繼續旋轉新的這對射線以獲得新的對踵點
當我們枚舉了所有角度的平行線之後,自然也就枚舉出了所有對踵點
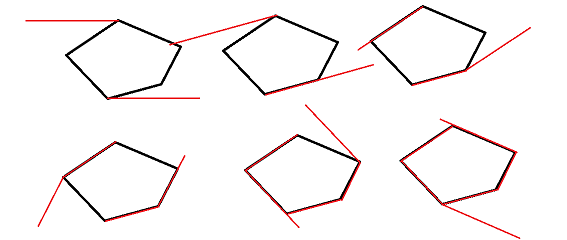
列舉角度的效率是INF的(十分高效)
然而並不是所有角度的平行切線都切與不同的對踵點,所以在轉動的過程中有許多角度可以直接略過
具體地說,同一角速度轉動這一說法太過玄學,具體實現應該是,
把上述過程按照兩個射線的頂點是否有其一被替代來劃分為許多階段,
可以通過叉積來判定$\overrightarrow {pp_{next}}$和$\overrightarrow{q_{next}q}$的極角大小,
進而確定p與q被替代的先後順序
然後直接在兩個階段之間跳躍,因為這期間沒有新的對踵點產生
3.2.1.求凸多邊形的直徑:
凸多邊形的直徑是凸多邊形邊上所有點中距離最遠的一對點的距離,
他顯然是某對對踵點的距離,列舉所有對踵點即可
效率$O(n)$(對每一對對踵點O(1))

double RotatingCaliper_diameter(Point poly[],int n){ int p=0,q=n-1,fl,i; double ret=0; for(i=0;i<n;i++){ if(poly[i].y>poly[q].y) q=i; if(poly[i].y<poly[p].y) p=i; } Point ymin=poly[p],ymax=poly[q]; for(i=0;i<n*3;i++){ if(ret<Length(poly[p%n]-poly[q%n])) ret=Length(poly[p%n]-poly[q%n]); fl=dcmp(Cross(poly[(p+1)%n]-poly[p%n],poly[q%n]-poly[(q+1)%n])); if(!fl){ if(ret<Length(poly[p%n]-poly[(q+1)%n])) ret=Length(poly[p%n]-poly[(q+1)%n]); if(ret<Length(poly[q%n]-poly[(p+1)%n])) ret=Length(poly[q%n]-poly[(p+1)%n]); p++,q++; } else{ if(fl>0) p++; else q++; } } return ret; }//用旋轉卡殼求解凸多邊形直徑R.C_diameter
習題:
POJ P2187——需要求凸包,然後求凸包的直徑的平方輸出
3.2.2.求凸多邊形的寬度:
凸多邊形的寬度是凸多邊形的所有平行切線對的距離的最小值
對任意一對平行切線$l_1^a,l_2^a$,必有一對平行切線$l_1^b,l_2^b$,其中至少一條與某一整條邊重合
滿足$dis(l_1^b,l_2^b)<=dis(l_1^a,l_2^a)$
於是列舉此類平行切線即可
由於,旋轉卡殼的過程正是由出現此類平行切線的時間點來劃分的,所以可以列舉所有此類平行切線
效率$O(n)$(對每一對對踵點O(1))

double RotatingCaliper_width(Point poly[],int n){ int p=0,q=n-1,fl,i; double ret; for(i=0;i<n;i++){ if(poly[i].y>poly[q].y) q=i; if(poly[i].y<poly[p].y) p=i; } ret=Length(poly[p]-poly[q]); for(i=0;i<n*3;i++){ fl=dcmp(Cross(poly[(p+1)%n]-poly[p%n],poly[q%n]-poly[(q+1)%n])); if(!fl){ if(ret>DistanceToLine(poly[p%n],poly[q%n],poly[(q+1)%n])) ret=DistanceToLine(poly[p%n],poly[q%n],poly[(q+1)%n]); p++,q++; } else{ if(fl>0){ if(ret>DistanceToLine(poly[q%n],poly[p%n],poly[(p+1)%n])) ret=DistanceToLine(poly[q%n],poly[p%n],poly[(p+1)%n]); p++; } else{ if(ret>DistanceToLine(poly[p%n],poly[q%n],poly[(q+1)%n])) ret=DistanceToLine(poly[p%n],poly[q%n],poly[(q+1)%n]); q++; } } } return ret; }//用旋轉卡殼求解凸多邊形寬度Rotating Caliper Width
(沒找題,正好yhzq大神做的某次比賽有這個題,正好用那個題實驗了板子的正確性2333)
3.2.3.求凸多邊形的最小面積外接矩形:
這樣的矩形一定與凸多邊形至少一邊發生重合,於是這一條重合的邊以及這條邊的對邊可以通過旋轉卡殼來列舉,
在枚舉出這麼一組有重合平行邊之後,如何列舉另外一對平行邊呢,
在我們枚舉出第一對有重合平行邊並找到其對應的另一對邊之後(這個另一對邊方向與有重合平行邊垂直,所以這對邊其實可以存成多邊形上的一對點)
如果我們旋轉這組有重合平行邊得到另一組有重合平行邊的話,
新的一組的對應另一對邊可以由舊的一組通過向相同的方向旋轉得來,
判定是否完成旋轉的方法可以是向量叉積
效率$O(n)$(對每一對對踵點O(1),另一對平行線的旋轉也是單向的於是也是O(n))
其實求最小周長外接矩形也是同理

void RC(Poi poly[],int n){ int p=0,q=n-1,l=0,r=n-1; int fl,i,j; Vec nm,dr; for(i=0;i<n;i++){ if(poly[i].y<poly[p].y) p=i; if(poly[i].y>poly[q].y) q=i; if(poly[i].x<poly[l].x) l=i; if(poly[i].x>poly[r].x) r=i; } an[0]=intersect_p(poly[p],Vec(1,0),poly[l],Vec(0,1)),an[1]=intersect_p(poly[p],Vec(1,0),poly[r],Vec(0,1)); an[2]=intersect_p(poly[r],Vec(0,1),poly[q],Vec(1,0)),an[3]=intersect_p(poly[l],Vec(0,1),poly[q],Vec(1,0)); ans=fabs(Area(an[0],an[1],an[2])); for(i=0;i<n*3;i++){ fl=dcmp(Cross(poly[(p+1)%n]-poly[p%n],poly[q%n]-poly[(q+1)%n])); if(!fl){ dr=poly[(p+1)%n]-poly[p%n],dr=dr/Len(dr); nm=Vec(dr.y,-dr.x); while(dcmp(Cross(poly[(l+1)%n]-poly[l%n],nm))>0) l++; nm=Vec(0,0)-nm; while(dcmp(Cross(poly[(r+1)%n]-poly[r%n],nm))>0) r++; cha[0]=intersect_p(poly[p%n],dr,poly[l%n],nm),cha[1]=intersect_p(poly[p%n],dr,poly[r%n],nm); cha[2]=intersect_p(poly[r%n],nm,poly[q%n],dr),cha[3]=intersect_p(poly[l%n],nm,poly[q%n],dr); if(fabs(Area(cha[0],cha[1],cha[2]))<ans){ for(j=0;j<4;j++) an[j]=cha[j]; ans=fabs(Area(an[0],an[1],an[2])); } } else{ if(fl>0){ dr=poly[(p+1)%n]-poly[p%n],dr=dr/Len(dr); nm=Vec(dr.y,-dr.x); while(dcmp(Cross(poly[(l+1)%n]-poly[l%n],nm))>0) l++; nm=Vec(0,0)-nm; while(dcmp(Cross(poly[(r+1)%n]-poly[r%n],nm))>0) r++; cha[0]=intersect_p(poly[p%n],dr,poly[l%n],nm),cha[1]=intersect_p(poly[p%n],dr,poly[r%n],nm); cha[2]=intersect_p(poly[r%n],nm,poly[q%n],dr),cha[3]=intersect_p(poly[l%n],nm,poly[q%n],dr); if(fabs(Area(cha[0],cha[1],cha[2]))<ans){ for(j=0;j<4;j++) an[j]=cha[j]; ans=fabs(Area(an[0],an[1],an[2])); } p++; } else{ dr=poly[(q+1)%n]-poly[q%n],dr=dr/Len(dr); nm=Vec(-dr.y,dr.x); while(dcmp(Cross(poly[(l+1)%n]-poly[l%n],nm))>0) l++; nm=Vec(0,0)-nm; while(dcmp(Cross(poly[(r+1)%n]-poly[r%n],nm))>0) r++; cha[0]=intersect_p(poly[p%n],dr,poly[l%n],nm),cha[1]=intersect_p(poly[p%n],dr,poly[r%n],nm); cha[2]=intersect_p(poly[r%n],nm,poly[q%n],dr),cha[3]=intersect_p(poly[l%n],nm,poly[q%n],dr); if(fabs(Area(cha[0],cha[1],cha[2]))<ans){ for(j=0;j<4;j++) an[j]=cha[j]; ans=fabs(Area(an[0],an[1],an[2])); } q++; } } } }Minimum external rectangle area
習題:
bzoj P1185==luogu P3187 [HNOI2007]最小矩形覆蓋
(luogu沒有SPJ,卡精度;BZOJ輸出九個nan不知還能不能過)
3.3.凸包部分:
凸包的定義前面已經給出了,並沒有什麼值得強調的
值得一提的是某個問題——
定義一個物品集有n個物品,每個物品完全由一個大小為m的元素集中的一些元素按照某個比例融合而成
設在i物品中j元素佔比為$x_{i,j}$
則有$\sum_{j=1}^mx_{i,j}=1(i=1...n)$
每次詢問給出一種新的物品中各元素的佔比,問他能否被原來物品集中的物品按一定比例融合來得到
這個問題在m為2時可以看做一個點是否在凸包內的判定問題
m為3時可以看做一個點是否在一個三維凸包內的判定問題
。。。
好吧,我們還是先看看二維凸包的求法吧
3.3.1.凸包、凸殼的求法——Andrew演算法:
求凸包,實際是求在凸包邊上的端點,或者說,是求凸殼的過程
其流程是:
先把所有點按x為第一關鍵字,y為第二關鍵字排序然後去重
然後將第一第二個點加入凸殼,
從第三個點開始,
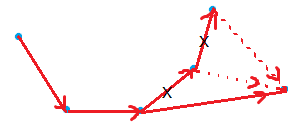
當新加入可能是凸殼第i個點的$p_i$時,判定$p_{i-1}$是否需要被剔出凸殼
若連續線段$\overline{p_{i-2}p_{i-1}}$和$\overline{p_{i-1}p_i}$是向順時針偏折的,則把$p_{i-1}$剔出凸包,
然後繼續判定$p_{i-2}$是否需要被剔出凸包......直到當我們判定$p_j$時,發現他不需要被剔出凸包,
然後把$p_i$放入凸殼,發現他現在可能是凸殼第j+1個點(當然咯,也可能什麼都不是)
然後繼續加入凸殼的第j+2個點,重複上述過程
當我們結束對n的處理後,我們得到了一個下凸殼——他的每條線都成下凸的趨勢
這樣再從n開始倒著來一遍就求出了上凸殼,合起來就是完整的凸殼啦
時間複雜度為排序的O(nlogn).

int ConvexHull(Point*inp,int n,Point*outp){ sort(inp,inp+n); int m=-1,k,i,j; for(i=0;i<n;i++){ while(m>0&&Direction(outp[m-1],outp[m],inp[i])<=0)m--; outp[++m]=inp[i]; } k=m; for(i=n-2;i>=

