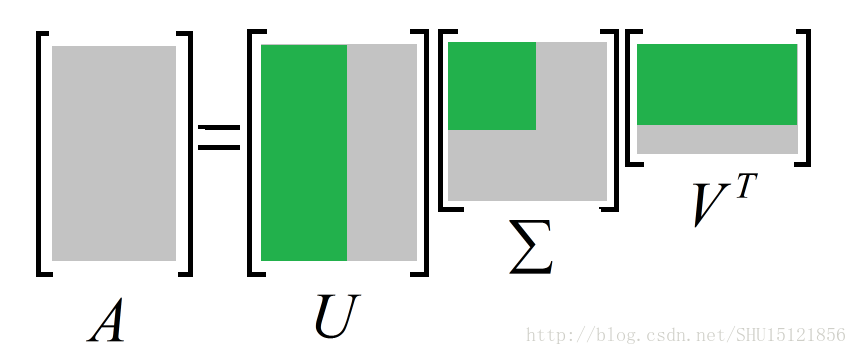矩陣乘以向量的幾何意義

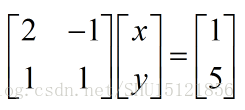
實際上也就是

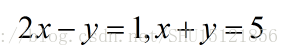
所以，它還可以寫成

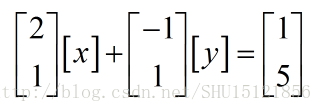
那麼把原來的矩陣按照列檢視來看，也就是

而[x]和[y]作為1x1的矩陣，在剛剛那個式子裡可以看成一個標量，也就變成了

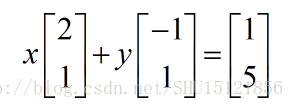
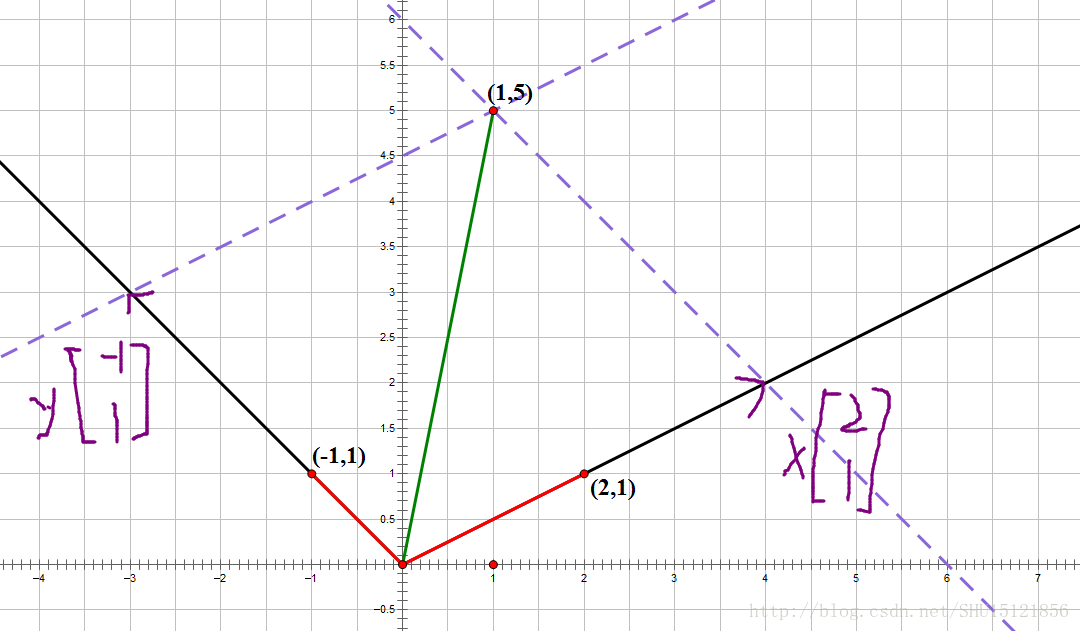
所以矩陣乘以一個列向量，可以看成把這個列向量的每一個分量當做一個權重，而把剛剛那個矩陣分成幾個列向量，用這些權重去對這些分解出的列向量做一定的線性組合，然後得到了一個新的列向量。
而(x,y)也就可以看成(1,5)這個向量在(2,1)向量和(-1,1)向量為單位構成的座標系上的座標。

方陣的特徵值和特徵向量

如果對於方陣A，存在一個列向量x，滿足Ax=λx，則x就是矩陣A的特徵向量，而λ是相應的特徵值。

一個例子

比如對於方陣A，我們去看一下A矩陣乘以這三個向量得到的向量：

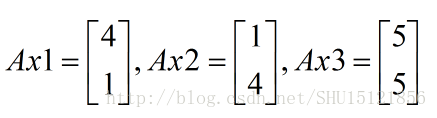
顯然Ax1,Ax2是找不到一個對應的λ使得前面的等式成立的，而對於Ax3可以找到λ=5，所以x3是A的一個特徵向量，5就是對應的特徵值。

幾何意義

對於列向量x，在其前面乘以了這個方陣A相當於對向量進行了旋轉和縮放：

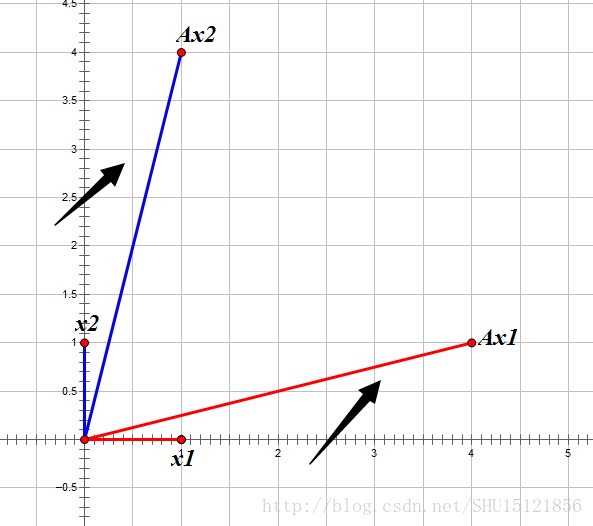
在上圖中可以看到，x1和x2經過方陣A給予的旋轉縮放後，所得向量和之前的列向量並不共線，所以找不到一個特徵值λ。而對於x3這個向量：

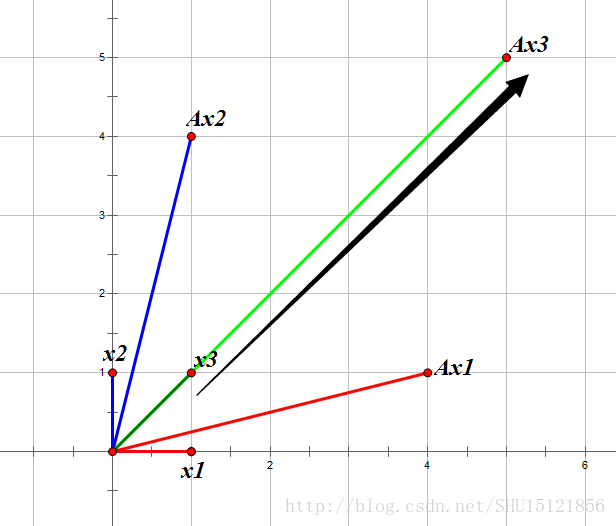
經過方陣A給予的旋轉縮放後，所得向量和之前的列向量(x3)是共線的，所以就能找到一個常數λ，作為這個縮放的方向和倍數，這裡λ=+5也就是與x3同方向放大了5倍。

初識SVD

SVD(矩陣的奇異值分解)是機器學習中一個重要的降維演算法。假如有這樣一個矩陣，每一行表示一個文字，這個文字中只可能出現n種單詞，在這行記錄每一個單詞的出現次數，也就形成了一個矩陣：

列數n可能會非常大，也就是每一行對應的向量維數會很大，不便於處理。我們想把它截短成一個較小的長度，實際上也就是降維的工作。
SVD所做的也就是把這個原始矩陣拆分成三個矩陣相乘的形式：

中間的矩陣是一個對角矩陣，表示原來資訊矩陣中的特徵和向量(也就是行和列)相關的重要程度。對這個對角矩陣Σ的主對角元排一下序(從左上角到右下角從大到小排序)，然後從中截取出左上角的一個小方陣：

因為剩下的那些主對角元都比較小，乾脆就把它們刪去，這樣之前一個比較大的對角矩陣就變成了一個比較小的對角矩陣。因為它的行和列壓縮了，相應地，第一個矩陣的列數和第三個矩陣的行數也會被壓縮，這樣就把原來的資訊矩陣的列數壓縮(每一行的向量降維)了。

矩陣運算的優勢

因為矩陣運算在底層有優化(例如學過的矩陣連乘的優化演算法)，所以在機器學習中儘量將多重迴圈等複雜的運算變成矩陣運算的方式，能優化效能。
比如之前學習過的得分函式的一個簡單例子，Function(色澤,口感,…,大小)=w0+w1*色澤+w2*口感+..+wn*大小，那麼權重w1~wn就是一個列向量，而每個商家的蘋果的特徵構成了一個矩陣，所做的正是矩陣乘以這個列向量(矩陣列檢視下列向量根據這個權重列向量的線性組合)。

類似地，算損失函式也可以用矩陣運算來做，更快更好。