如何快速設計一個FIR濾波器(二)通俗易懂,膜拜
一、理想低通濾波器單位脈衝響應是什麼樣
在如何快速設計一個FIR濾波器(一)中,我們介紹了一種簡單設計FIR的方法——零極點法。這個方法非常簡單,稍加培訓,用筆和紙就能完成;當然缺點也很顯而易見:零極點設計出的濾波器,只能給出大概的頻率響應,對於一些要求較高的系統,顯得無能為力。今天我們介紹一種更加嚴謹的方法。
現在假設我們要設計一個低通濾波器,截止頻率為 ,其理想頻率響應可以用如下函式表示:
則該濾波器的脈衝響應為:
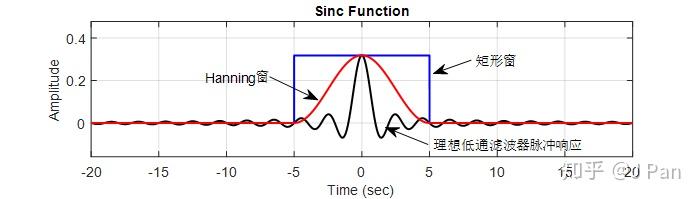
可見脈衝響應為一個sinc函式。畫出來大概張這個樣子:
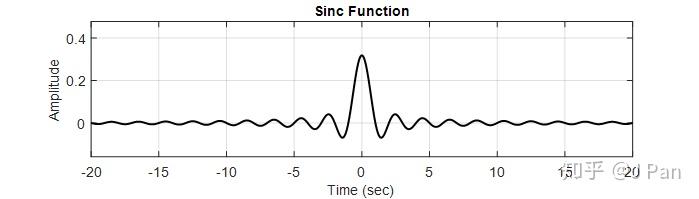
這個函式非常重要哦,建議都自己手動推導一下,非常有意思,我們把幅值最大的那一瓣稱之為主瓣,剩下稱之為從瓣,是不是很形象呢?注意主瓣的週期是從瓣的2倍哦。
可能你已經看見了,脈衝響應是由無窮多個——不對呀,我們是想設計一個有限脈衝響應的,結果出現了無窮多個響應,這可如何搞?——既然臣妾做不到把所有的脈衝響應都用上(因為我是有限脈衝濾波器FIR啊),那我只能擷取有限一部分進行代替了,也就是——加窗。
窗函式這個東西很不好理解,我們就多花點功夫說說這個事。
二、什麼是加窗
現在假設有一個函式,表示式為 ,為簡單起見,令
,
,很顯然,餘弦函式的頻域包含兩個分量

假如我們現在以10Hz的頻率進行取樣,顯然是滿足香濃取樣定理的,取樣脈衝及其頻譜如下圖:
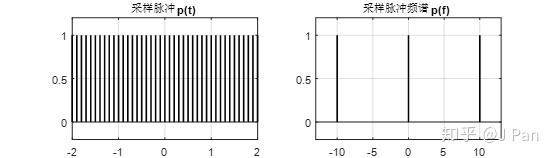
取樣過程就是拿取樣訊號和原始訊號進行乘積,那取樣之後的訊號長啥樣呢?
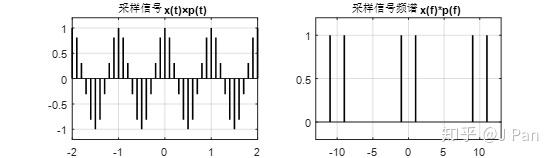
上圖即為取樣後的訊號及其頻譜。注意:此時取樣後的訊號是在時域無限擴充套件的,頻譜也一樣。但實際的計算中是不可能處理無窮多數量的訊號的,那怎麼辦呢?——截短唄,只觀察一部分樣本行不?貌似我們也沒有更好的選擇了。
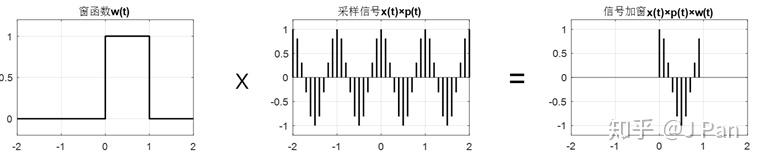
那怎麼截短呢?最簡單的方式就是矩形函數了,如下圖所示:
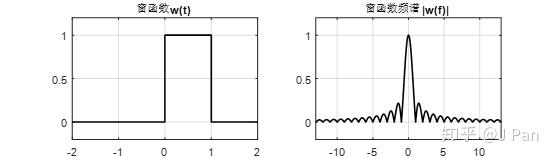
矩形函式的方法簡單粗暴,只保留一部分(幅值為1),其餘全部設為0,然後那矩形函式和取樣訊號相乘,就得到加窗(矩形窗)之後的取樣訊號了。矩形訊號的頻譜就是我們熟悉的sinc函式。加窗之後的取樣訊號及其頻譜如下:
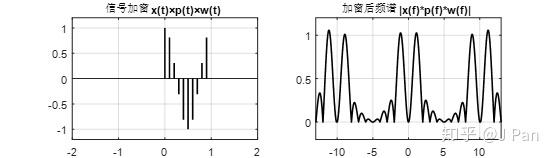
加窗後的離散餘弦訊號可以看成窗函式(矩形,頻譜為sinc函式)與餘弦離散訊號的乘積。那在頻域呢就是sinc函式和餘弦頻譜的卷積。看一個圖就明白加窗後的頻譜是怎麼來的了:
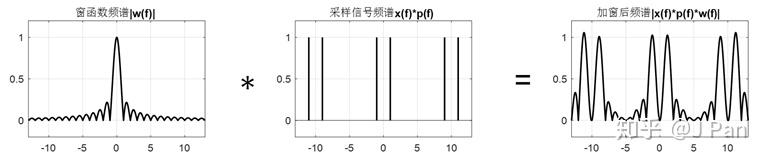
可以看出,由於加窗行為,頻譜中頻率成分變複雜了,由於矩形窗函式的頻譜是無限寬的,在頻譜的最大值處也出現了一定的畸變(略大於1)。這種有限長的離散訊號在時域中計算機是可以處理(離散的),但是在頻域還是不能,因為還是連續訊號。在如何理解離散傅立葉變換及Z變換一文中,我們介紹了將有限長的訊號進行週期延拓,就得到一個週期的離散訊號,其傅立葉變換也是週期離散的,這樣就可以在計算機中處理了。關於離散傅立葉變換,可以參照:
現在問題就變成了如何進行週期延拓——卷積,什麼意思呢?我們現在找一個取樣脈衝,時域中週期和加窗後的取樣訊號的週期一致(都是1),其形貌如下圖(左)所示:
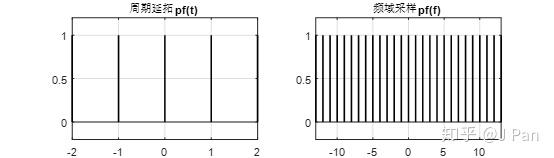
我們已經知道,週期延拓取樣脈衝的頻譜仍未取樣脈衝如上圖(右)所示。現在就可以做一個有意思的事情:週期延拓在數學上可以看成是一個有限長的訊號(長度即為週期)和一個同樣週期的無限長取樣脈衝的卷積。什麼意思呢?看一個圖就一目瞭然了:
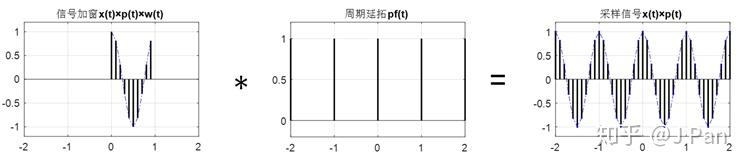
感興趣的可以用卷積的數學定義推導一下看看是不是這樣,很簡單的。由卷積定理我們知道,卷積和乘積在時域和頻域是對偶的,也就是說剛才我們所做的週期延拓(時域卷積)在頻域是乘積哦,具體如下圖所示。
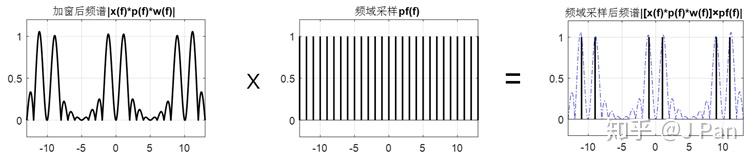
所以最終得到的經過週期延拓的加窗訊號及其頻譜如下圖所示。可以看出,進過週期延拓,加窗導致的頻譜洩漏似乎得到了抑制,加窗對頻譜沒什麼影響。
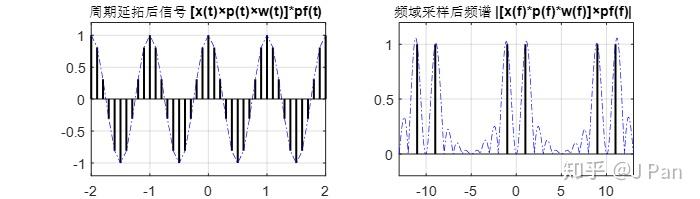
事實是不是這樣呢?——直覺告訴我們應該不是。我們之所以最終得到這個結論,是因為我們選的初始函式太簡單了。餘弦函式是週期訊號,頻譜是有限寬度的,如果窗函式的寬度是訊號週期的整數倍,則頻域取樣(時域週期延拓)將正好採在sinc函式的從瓣取值為零的地方,洩漏的頻譜沒有采到而已,具體如下圖所示。
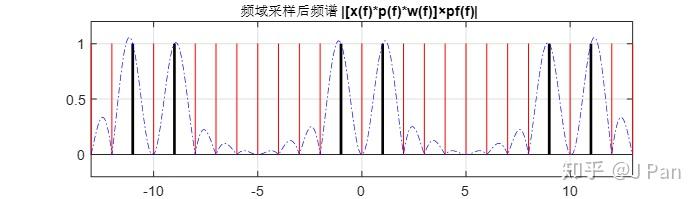
可能心細有童鞋會有疑問,為啥主瓣的最大值會有一定的偏移?——原因就是sinc函式主瓣和從瓣的週期不一樣,卷積時主瓣與從半疊加,最大值就偏移了。
實際工程中,我們可能不知道被處理訊號的週期,或者壓根就不是週期的訊號,那會出現什麼呢?現在假如我們把窗函式加寬,比如增加到原來的1.4倍,如下圖所示:
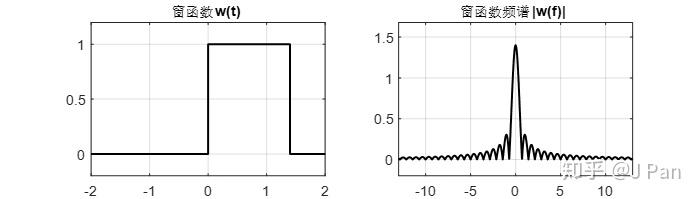
則可以得到加窗後的訊號及頻譜為:
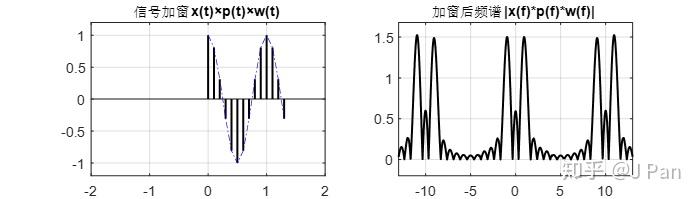
加窗並進行週期延拓後的訊號及頻譜為:
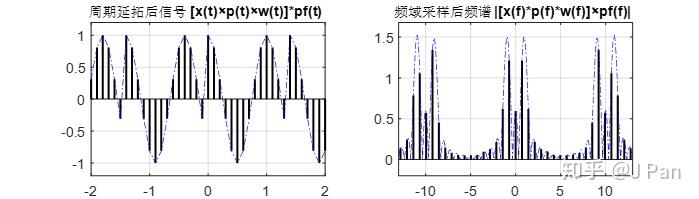
可見,由於窗函式寬度和原訊號週期不一致,加窗後的訊號進行週期延拓時出現了不連續,頻域取樣時不像前面那樣只採集到sinc為零的地方,頻譜出現了較大的洩漏,如下圖所示。
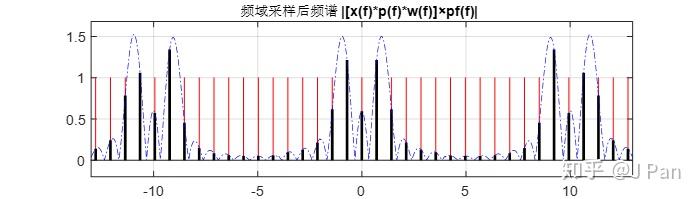
實際工程上絕大多數訊號都不是週期訊號,也不是有限長訊號,而是我們只能觀察有限長度而已。要想不出現頻譜洩漏,需要窗函式長度是被處理訊號頻譜所有分量的整數倍,這幾乎是不能達到的。因此加窗後,頻譜洩漏是不可避免的,只能儘量減小。
本節中所用的算例來自 離散傅立葉變換DFT基本原理圖解 ,感興趣請前往閱讀。
三、窗函式都有哪些
最開始我們介紹了一個理想的低通濾波器,在頻域內其幅值響應是一個矩形。這個矩形進行傅立葉逆變換,發現單位衝擊響應有無窮多個,我們沒辦法,用了一個矩形窗進行截短,注意著兩個矩形不是同一個事情哦,一個是幅值響應(頻域),一個截短函式(時域),只不過樣子都呈現矩形。
現在我們都放在頻域來看:首先時域矩形函式在頻域為sinc函式,時域的矩形函式截短(乘積)在頻域對應卷積。也就是說在頻域裡,脈衝響應截短後的濾波器頻域幅值響應是矩形訊號和sinc訊號的卷積,仔細想想這段話哦!下圖展示了卷積之後的訊號的樣子。
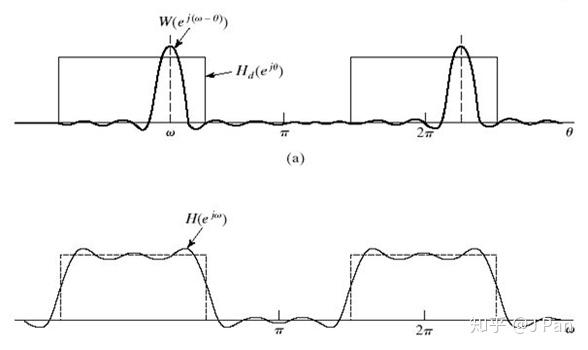
可以想象:假設窗函式寬度無窮大,則對應的sinc函式無窮窄,則卷積之後的函式非常接近理想矩形;反之,若窗函式很窄,在sinc函式就會變得很寬,則卷積之後的函式與理想矩形差別就比較大,這就是傳說中的不確定原理哦,具體可參照:
那什麼樣的窗函式比較好呢?——在頻域看就是要能量相對集中,也就是旁瓣要低。因為出現洩漏的主要原因就是窗函式的頻譜是無限長的,與訊號的頻譜卷積時,主瓣與從瓣會出現疊加,因此從瓣的能量越小,影響就越小。在時域看就是加窗後的函式在進行週期延拓時儘量不要有非連續,因為非連續就需要很多分量來模擬,就造成了頻譜洩露。那什麼樣函式的頻譜主瓣能量較集中呢?——主要有以下是幾種常見的窗函式:矩形窗、漢寧窗、漢明窗、凱撒窗等。
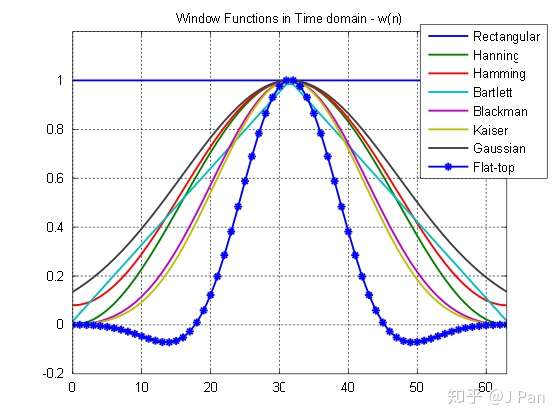
這些窗函式對應的頻譜分別為:
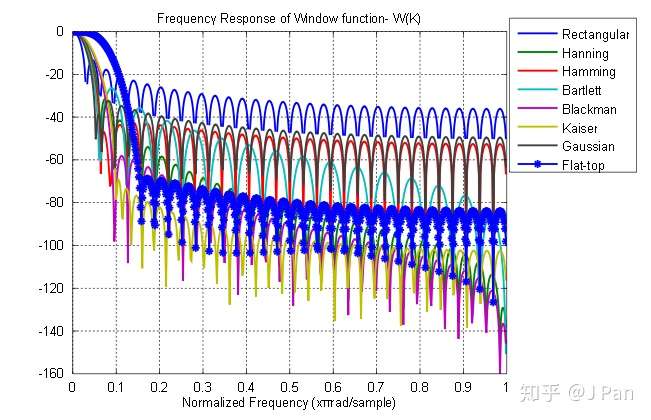
現在我們拿漢寧窗(Hanning)來舉個例子。還是原來的餘弦函式 ,
,
。假設窗函式的寬度
,Hanning窗窗函式及其頻譜為:
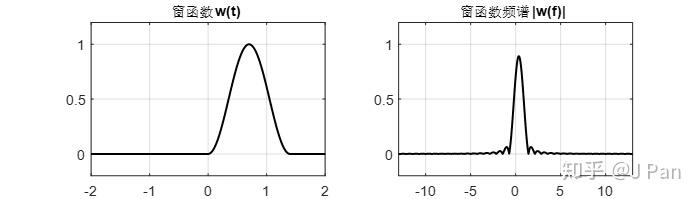
可見其頻譜中主瓣能量與矩形窗比,集中了很多。餘弦訊號取樣、加窗之後的訊號及其頻譜為:
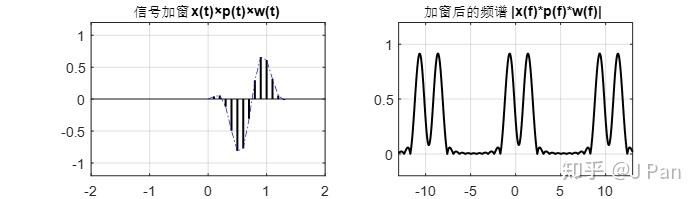
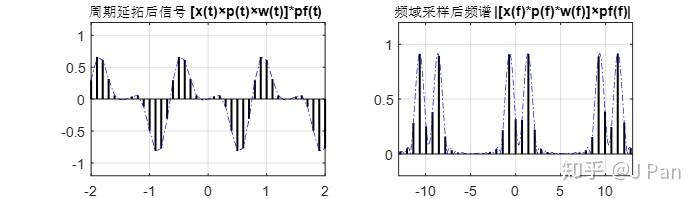
由於Hanning窗從零開始,結束的時候也是零,因此加窗之後的訊號開始和結束也都是零,連續性好了,從頻譜看,洩漏也少了。這個從週期延拓後(DTFT)的訊號與頻譜看的更清楚。
四、如何基於窗函式法設計FIR
這篇文章中,我們主要說怎麼較為精確的設計一個FIR,我們花了大量篇幅說了窗函式,這是因為窗函式在實際的工程應用中很多,比如基於窗函式的FIR就是FIR設計中最廣泛運用的一個方法。接下來,我們要介紹一下什麼是用窗函式設計FIR。
在文章開始的時候,我們已經介紹了,對於理想低通濾波器,其脈衝響應為sinc函式,且有無窮多個,我們必須加窗才能處理,加窗就會有一定的頻譜洩漏,因此實際設計出來的濾波器和理想濾波器還是有差別的。
基於窗函式的FIR設計就是通過選擇合適常函式來找到滿足要求的濾波器,一般步驟是這樣的:
1)確定頻域的響應函式 ,低通、高通、帶通或者其他;
2)確定頻域的響應函式 的傅立葉逆變換,找到連續脈衝響應函式
;
3)對脈衝響應函式 按照一定的取樣頻率進行取樣,獲得離散訊號
;
4)選擇合適的窗函式,對離散訊號 加窗,獲得有限長度的脈衝響應
;
當然實際實踐中,我們只需要知道這個過程,具體細節不需要我們考慮,因為MATLAB提供了一個強大的函式,幫我們都做好了——fir1。
fir1的基本語法如下:h = fir1(n,Wn,ftype,window)
其中n表示濾波器的階數(order),Wn表示歸一化後的濾波器的截止頻率,可表示成 的形式。舉個例子,比如一個帶狀濾波器,取樣頻率
是200Hz,兩個截止頻率分別為10Hz和50Hz,則
,即截止頻率除以
。ftype表示濾波器型別,可以是lowpass, highpass, bandpass, bandstop, or multiband filter。window表示窗函式型別,前面我們列到的窗函式都可以選擇。h為所設計的濾波器的係數。
舉個簡單的例子:
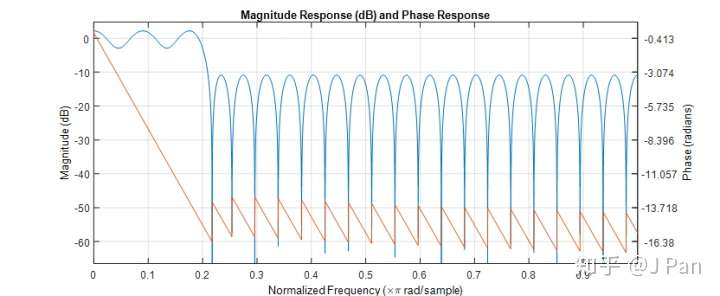
h = fir1(48,[0.35 0.65]);
freqz(b,1,512)
這是一個48階的帶通濾波器,歸一化的截止頻率為[0.35 0.65],其幅值響應和相位響應如下圖所示。
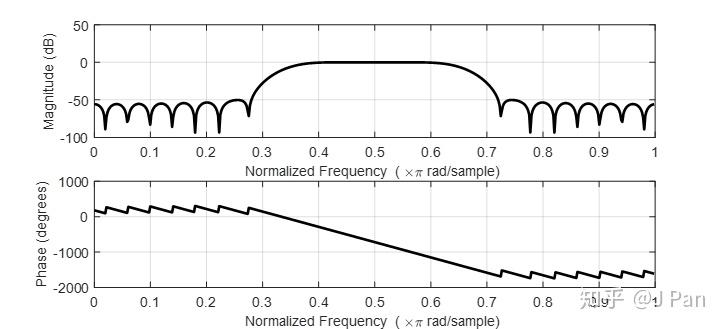
可見,採用fir1函式設計FIR濾波器非常方便。
除了fir1函式,fir2函式也有時候會用到,fir2函式是什麼意思呢?——我們稱之為基於頻率取樣法的設計方法,具體做法就是:把濾波器期望的幅值響應用一組分立的點 來表示,
表示頻率為
時的期望幅值響應,然後在不同的點之間進行線性插值,得到完成的期望幅值響應,然後進行傅立葉逆變換並用Hamming(漢明窗)截短來獲得濾波器的係數。
基本語法為:h = fir2(n,f,m)
n表示濾波器階數,f表示分離點的向量,m表示分立點對應的幅值響應向量,舉個例子就明白了。現在要設計一個低通濾波器,幅值響應如下圖所示:
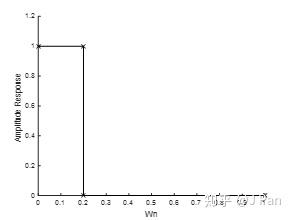
顯然四個特徵點的座標分別為(0,1), (0.2,1), (0.2,0), (1,0) ,於是我們可以獲得分立點的向量為f=[0 0.2 0.2 1] ,對應幅值響應向量為m=[1 1 0 0]。
f=[0 0.2 0.2 1] ;
m=[1 1 0 0];
h = fir2(48,f,m);
freqz(b,1)
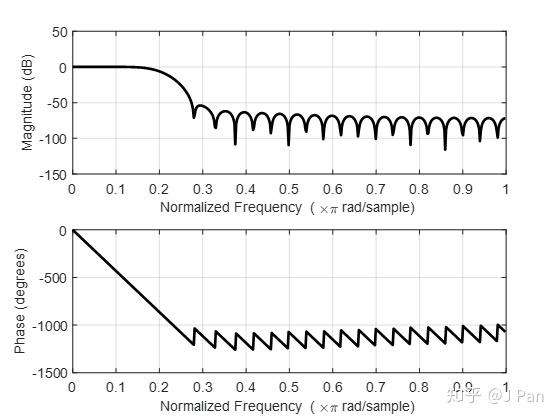
五、如何基於響應最優法設計FIR
前面我們說了兩種基於窗函式的方法,主要是用窗函式對無限長的脈衝進行截短,獲得近似的頻域響應。除了窗函式法,還有另外的一種解決方案也比較常用,我們稱之為“最優法”,主要思路就是找到一組脈衝響應,讓它的頻域響應 與期望的濾波器的頻域響應
儘可能的一致,主要通過兩種方法來實現,一個是最小二乘法,另一個是切比雪夫法。
(一)最小二乘法
與頻率取樣法近似,期望的頻率響應用一組分立的點 來表示,在不同的點之間進行插值,然後來尋找濾波器的係數
時期滿足
其中 為不同頻率下的權重。
MATLAB指令為:h=firls(n,f,m)
n為濾波器階數,f表示分離點的向量,m表示分立點對應的幅值響應向量。仍以前面說的低通濾波器為例:
f=[0 0.2 0.2 1] ;
m=[1 1 0 0];
h = firls(48,f,m);
freqz(b,1)
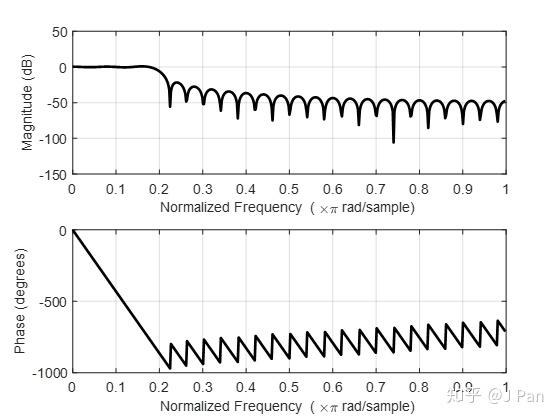
(二)切比雪夫法(又叫帕克斯-麥克勞林法)
與最小二乘法不同(方差最小),切比雪夫法採用的方案是最大誤差最小,即:
MATLAB指令為:h=firpm(n,f,m)
n、f、m定義和前面一致,不同的是頻率響應在同一頻率下必須去不同的值。前面的例子中當頻率為0.2(歸一化後)時,頻率響應可直接從1降到0,對於切比雪夫法,規定不能這樣做,我們將第二個0.2改為0,21。
f=[0 0.2 0.21 1] ;
m=[1 1 0 0];
h = firpm(48,f,m);
freqz(b,1)
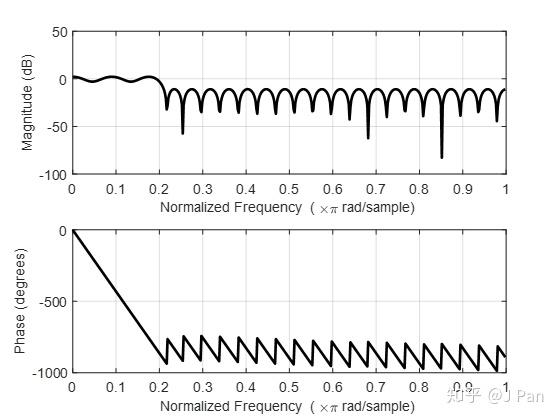
六、如何利用MATLAB設計FIR濾波器
要想快速設計一個FIR濾波器,MATLAB可以說是一個最有利的幫手,當你知道較多濾波器知識和相關函式時,可以直接呼叫函式進行設計,靈活且方便。當你不知道時,也沒有關係,開啟MATLAB,在命令列輸入:filterDesigner或者fdatool(老版MATLAB),你就能看到如下介面:
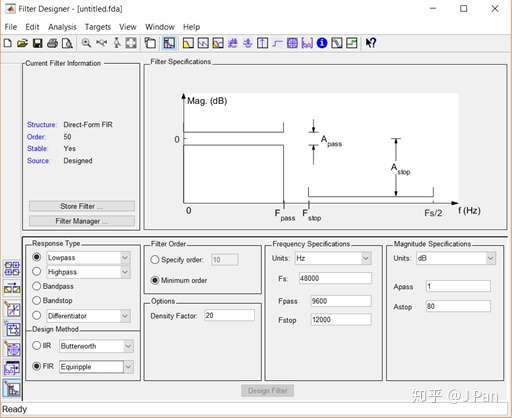
通過勾勾選選就能設計濾波器哦!
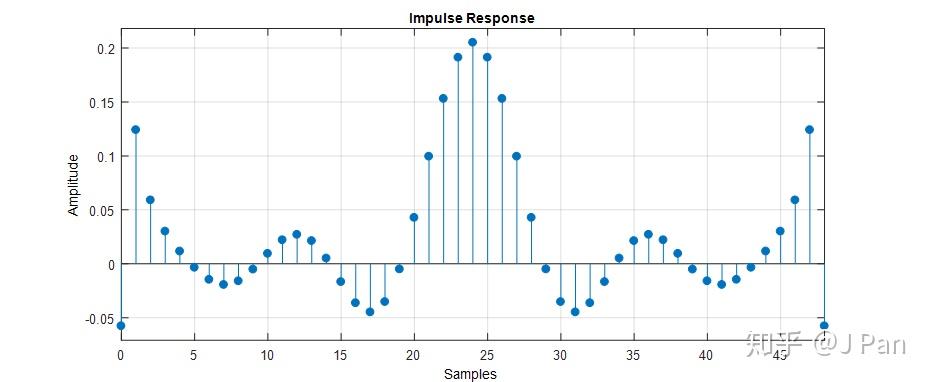
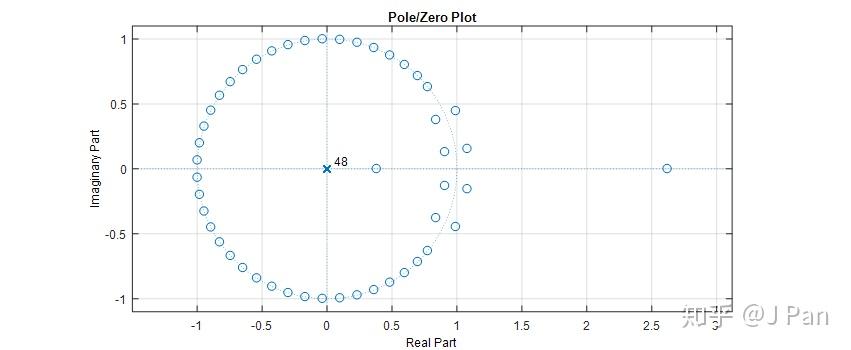
如果你又進步了一點,已經設計出一個濾波器,相看看效能怎麼樣,也簡單,開啟MATLAB,輸入:fvtool(h),h就是你設計的濾波器的係數,你就會看到各種你想要的濾波器特性:幅值響應、相位響應、脈衝響應、零極點等等。