在Spark2.0版本中（不是基於RDD API的MLlib），共有四種聚類方法：
     （1）K-means
     （2）Latent Dirichlet allocation (LDA)
     （3）Bisecting k-means（二分k均值演算法）
     （4）Gaussian Mixture Model (GMM)。
       基於RDD API的MLLib中，共有六種聚類方法：
     （1）K-means
     （2）Gaussian mixture
     （3）Power iteration clustering (PIC)

     （4）Latent Dirichlet allocation (LDA)**
     （5）Bisecting k-means
     （6）Streaming k-means
       多了Power iteration clustering (PIC)和Streaming k-means兩種。
       本文將介紹其中的一種高斯混合模型 ，Gaussian Mixture Model (GMM)。其它方法在我的Spark機器學習系列裡面，都會介紹。

       混合模型：通過密度函式的線性合併來表示未知模型p(x)
      為什麼提出混合模型，那是因為單一模型與實際資料的分佈嚴重不符，但是幾個模型混合以後卻能很好的描述和預測資料。
       高斯混合模型（GMM），說的是把資料可以看作是從數個高斯分佈中生成出來的。雖然我們可以用不同的分佈來隨意地構造 XX Mixture Model ，但是 GMM是最為流行。另外，Mixture Model 本身其實也是可以變得任意複雜的，通過增加 Model 的個數，我們可以任意地逼近任何連續的概率密分佈。
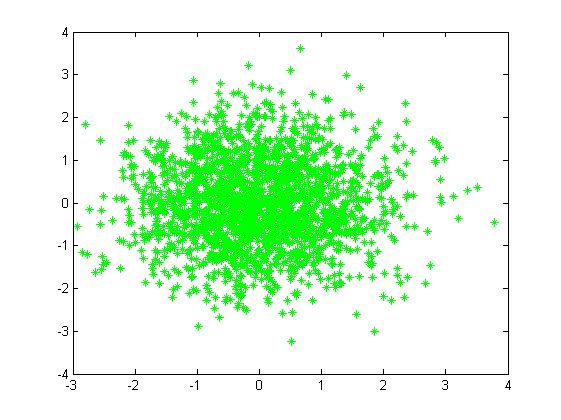
      二維情況下高斯分佈模擬產生資料的分佈是橢圓，如下圖：

      對於下面圖（a）觀測資料，單一的高斯概率分佈函式（一個橢圓）無法表達，仔細看圖（a）近似包含三個橢圓，所以可以將三個高斯概率分佈函式線性組合起來，各個函式有不同的引數N（σi,μi）和權重πi。線性組合

p(x|μi,σi,πi)=∑i=13πi12π−−√σiexp(−(x−μi)22σ2i)這樣就能計算所有樣本出現的概率了。圖（b）已經明確了樣本分類。

更一般地，GMM認為資料是從K個高斯函式組合而來的，即
p(x)=∑k=1KπkN(x;μk,σk)
隱含K個高斯函式，K需要首先確定好。
如果估計未知引數π,μ,σ,我們首先得分析以下最大似然估計：
∑i=1

Nlog{∑k=1KπkN(x;μk,σk)}
由於在對數函式裡面又有加和，我們沒法直接用求導解方程的辦法直接求得最大值。為了解決這個問題，採用了EM方法。
       EM演算法可參考我的另一篇文章
《機器學習演算法（優化）之二：期望最大化（EM）演算法》http://blog.csdn.net/qq_34531825/article/details/52856948.

EM演算法模型引數估計

每個GMM由K個Gaussian component分佈組成。我以一維Gaussian函式，GMM模型有3個隱含component為例，通俗的說明。
E過程：
假定我們通過迭代（或者初始化），假設已經已經知道了GMM模型的三個component Gaussian函式的引數θ(t)=（σ(t)1,μ(t)1）、（σ(t)2,μ(t)2）、（σ(t)3,μ(t)3），且這三個函式分別以π(t)1=0.3、π(t)2=0.3、π(t)3=0.4的概率被GMM模型選中（即π(t)i為第i個component的權重)。
高斯混合模型為p(x|θ)=0.3∗N(x;μ1,σ1)+0.3∗N(x;μ2,σ2)+0.4∗N(x;μ3,σ3)
迭代的第t步，對於觀測到的x點，那麼他究竟是3個隱含的Gaussina曲線中的那一個產生的呢？應該說都有可能，只是產生的概率大小不一樣而已。如圖中的x點，它由N(x;μ3,σ3)產生的可能性最大，概率為π3∗N(x;μ3,σ3)，假設為0.4*0.30=0.12，其次是π2∗N(