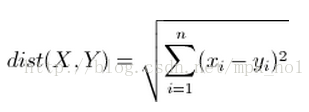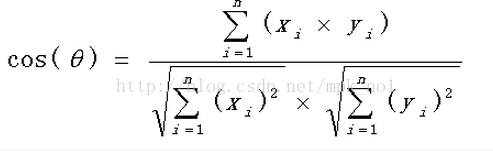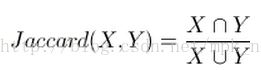文字相似度計算的幾個距離公式(歐氏距離、餘弦相似度、Jaccard距離、編輯距離)
本文主要講一下文字相似度計算的幾個距離公式,主要包括:歐氏距離、餘弦相似度、Jaccard距離、編輯距離。
距離計算在文字很多場景下都可以用到,比如:聚類、K近鄰、機器學習中的特徵、文字相似度等等。接下來就一一介紹一下:
假設兩個文字X=(x1, x2, x3,...xn)和Y=(y1, y2, y3, ..., yn),其向量表示分別為:Vec(X) = (v1, v2, v3, ... vp), Vec(Y) = (l1, l2, l3, ... lp)
1.歐式距離
歐式距離也稱歐幾里得距離,是最常見的距離度量,衡量的是多維空間中兩個點之間的絕對距離。
計算公式如下:
2.餘弦相似度
餘弦相似度用向量空間中兩個向量的夾角的餘弦值來衡量兩個文字間的相似度,相比距離度量,餘弦相似度更加註重兩個向量在方向上的差異,一般情況下,用Embedding得到兩個文字的向量表示之後,可以使用餘弦相似度計算兩個文字之間的相似度。
計算公式如下:
3.Jaccard距離
Jaccard距離用於計算符號度量或者布林值度量的兩個個體之間的相似度,由於個體的特徵屬性是用符號或者布林值度量的,所以只能統計包含的共同特徵個數。
計算公式如下:
4.編輯距離
編輯距離主要用來計算兩個字串的相似度,其定義如下:
設有字串A和B,B為模式串,現給定以下操作:從字串中刪除一個字元;從字串中插入一個字元;從字串中替換一個字元。通過以上三種操作,將字串A編輯為模式串B所需的最小運算元稱為A和B的最短編輯距離,記為ED(A,B)。
求解最短編輯距離的演算法描述如下:
用一個二維陣列ED[i][j]表示字串A的前i個字元編輯成字串B的前j個字元所需的最小運算元。則ED[i][j]的遞推公式為:
⑴ ED[i][0]=i,ED[0][j]=j,其中0≤i≤A.len,0≤j≤B.len;
⑵ 若A[i]=B[j],則ED[i][j]=ED[i-1][j-1];
⑶ 若A[i]≠B[j],則ED[i][j]=min(ED[i-1][j-1],ED[i][j-1],ED[i-1][j])+1。
編輯距離越小,說明兩個字串越相似。反之,越不相似。
以上只是距離計算公式的常見的四種,還有很多種距離計算公式,以後如果用到了會繼續添上。