邏輯迴歸(Logistic Regression, LR)是傳統機器學習中的一種分類模型，由於演算法的簡單和高效，在實際中應用非常廣泛。它的起源非常複雜，可以看參考引用1。具體應用實踐可以看這裡。

問題背景

對於二元分類問題，給定一個輸入特徵向量X$X$(例如輸入一張圖片，通過演算法識別它是否是一隻貓的圖片)，演算法能夠輸出預測，稱之為y^$\hat{y}$，也就是對實際值y$y$的估計。或者說，y^$\hat{y}$表示y$y$等於1的一種可能性或是置信度(前提條件是給定了輸入特徵X$X$)。

如果代入帶線性迴歸的模型中y^=wTx$\hat{y}=w^{T}x$：

假設輸入X$X$為腫瘤大小，上圖表示y$y$值大於0.5時演算法預測為惡性腫瘤，小於0.5時預測為良性腫瘤。看上去好像沒有什麼問題，但是在

LR模型

Sigmoid函式

所以對應條件概率分佈(二分類)P(Y|X)$P(Y|X)$為

引數求解

那麼我們該如何求救裡面的引數w$w$呢？常用的方法有梯度下降法,牛頓法和BFGS擬牛頓法。

梯度下降法

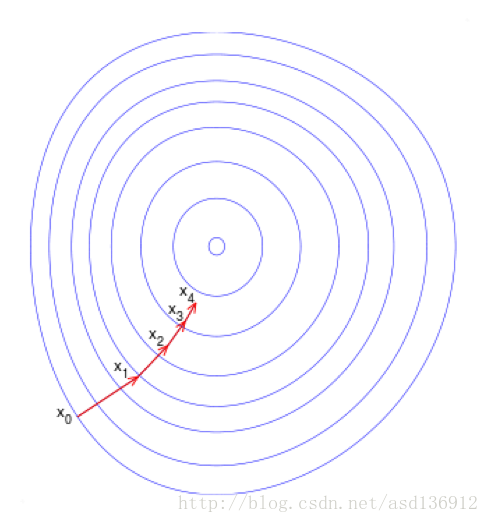
梯度下降(Gradient Descent)又叫作最速梯度下降，是一種迭代求解的方法，通過在每一步選取使目標函式變化最快的一個方向調整引數的值來逼近最優值。基本步驟如下：

1. 選擇下降方向（梯度方向，∇J(θ)$\nabla J(\theta )$）
2. 選擇步長，更新引數θi=θi−1−αi∇J(θi−
   1)${\theta }_i={\theta }_{i-1}-{\alpha }_i\nabla J({\theta }_{i-1})$
3. 重複以上兩步直到滿足終止條件
   
   我們首先定義一下損失函式Loss Function，如果我們使用常用的平方損失函式：
   L(y^,y)=12(y^−y)2$$L(\hat{y},y)=\frac{1}{2}(\hat{y}-y{)}^2$$
   得到的函式影象如下左圖，非凸函式有許多區域性最小值，將會影響梯度下降尋找全域性最小值。
   
   所以我們定義Lost Function為
   L(y^,y)=−(ylogy^+(1−y)log(1−y^))$$L(\hat{y},y)=-(ylog\hat{y}+(1-y)log(1-\hat{y}))$$
   Cost Function J$J$ (衡量演算法在全部樣本上的表現) 為：
   J=1m∑i=1m(y^(i),y(i))=
   相關推薦

   LR(Logistic Regression) 邏輯迴歸模型 進行二分類或多分類 及梯度下降學習引數

   邏輯迴歸(Logistic Regression, LR)是傳統機器學習中的一種分類模型，由於演算法的簡單和高效，在實際中應用非常廣泛。它的起源非常複雜，可以看參考引用1。具體應用實踐可以看這裡。 問題背景 對於二元分類問題，給定一個輸入特徵向量XX(例

   斯坦福Andrew Ng---機器學習筆記（二）：Logistic Regression(邏輯迴歸)

   內容提要 這篇部落格的主要內容有： - 介紹欠擬合和過擬合的概念 - 從概率的角度解釋上一篇部落格中評價函式J(θ)” role=”presentation” style=”position: relative;”>J(θ)J(θ)為什麼用最

   Logistic Regression(邏輯迴歸)

   分類是機器學習的一個基本問題, 基本原則就是將某個待分類的事情根據其不同特徵劃分為兩類. Email: 垃圾郵件/正常郵件 腫瘤: 良性/惡性 蔬菜: 有機/普通 　　對於分類問題, 其結果 y∈{0,1}, 即只有正類或負類. 對於預測蔬菜是否為有機這件事, y = 0表示蔬菜為普通,

   Logistic Regression--邏輯迴歸演算法彙總

   1.1邏輯迴歸模型 考慮具有p個獨立變數的向量,設條件概率為根據觀測量相對於某事件發生的概率。邏輯迴歸模型可表示為 　　　　　　　　　（1.1） 上式右側形式的函式稱為稱為邏輯函式。下圖給出其函式圖象形式。 其中。如果含有名義變數，則將其變為dummy變數。一個具有k個取值的名義變數，將變為k-1個d

   spark 2.x 原始碼分析 之 Logistic Regression 邏輯迴歸

   Logistic Regression 邏輯迴歸 注：第一次寫部落格，希望互相交流改進。如果公式顯示不完整，請看github原文 一、二元邏輯迴歸 1、簡介 迴歸是解決變數之間的對映關係（x->y），而邏輯迴歸則通過sigmoi

   Spark MLlib Logistic Regression邏輯迴歸演算法

   1.1 邏輯迴歸演算法 1.1.1 基礎理論 logistic迴歸本質上是線性迴歸，只是在特徵到結果的對映中加入了一層函式對映，即先把特徵線性求和，然後使用函式g(z)將最為假設函式來預測。g(z)可以將連續值對映到0和1上。 它與線性迴歸的不同點在於：為了將線性迴歸輸出的

   Logistic Regression(邏輯迴歸) +python3.6(pycharm)實現

   數學基礎知識略過，可自行查詢探究。遇到的bugs:1.AttributeError: module 'scipy' has no attribute '__version__'解決辦法:installed packages: 'scipy' :左上角File-- settin

   Logistic Regression 邏輯迴歸演算法例子，python程式碼實現

   轉載自原文 邏輯迴歸 Logistic Regression 雖然名字叫做邏輯迴歸 Logistic regression ，但它是一種分類演算法。對於文字處理方便，邏輯迴歸是一種非常強大的分類器。它主要通過在邏輯函式上執行迴歸來實現，正如其名字。 邏輯迴歸的一個小

   Logistic Regression邏輯迴歸的簡單解釋

   Logistic Regression也叫Logit Regression，在機器學習中屬於引數估計的模型。邏輯迴歸與普通線性迴歸（Linear Regression）有很大的關係。在應用上，它們有所區別： 普通線性迴歸主要用於連續變數的預測，即，線性迴歸的

   邏輯迴歸模型(Logistic Regression, LR)基礎

   邏輯迴歸(Logistic Regression, LR)模型其實僅線上性迴歸的基礎上，套用了一個邏輯函式，但也就由於這個邏輯函式，使得邏輯迴歸模型成為了機器學習領域一顆耀眼的明星，更是計算廣告學的核心。本文主要詳述邏輯迴歸模型的基礎，至於邏輯迴歸模型的優化、邏輯迴歸與計算廣告學等，請關注後續文章。 1

   機器學習演算法（一）：邏輯迴歸模型（Logistic Regression, LR）

   轉自：https://blog.csdn.net/weixin_39910711/article/details/81607386 線性分類器：模型是引數的線性函式，分類平面是（超）平面；非線性分類器：模型分介面可以是曲面或者超平面的組合。 典型的線性分類器有感知機，LDA，邏輯斯特迴歸，SVM

   邏輯迴歸模型（logistic regression）

   邏輯迴歸模型意義 邏輯迴歸是機器學習中做分類任務常用的方法，屬於“廣義的線性模型”，即： 考慮二分類任務，其輸出標記y∈{0，1},而線性迴歸模型產生的預測值 z = wx+b是實值，於是，需要將實

   為什麽邏輯斯特回歸(logistic regression)是線性模型

   softmax bsp 之間 ima 打破 regress 什麽 影響 線性變換 一個典型的logistic regression模型是: 這裏明明用了非線性函數，那為什麽logistic regression還是線性模型呢？ 首先，這個函數不是f(y,x)=0的函數

   LR模型（邏輯迴歸模型）

   1.邏輯迴歸模型 按照音譯logistic regression應該是邏輯斯蒂迴歸，太難聽了，就簡稱邏輯迴歸吧。 1.1 二項邏輯迴歸模型 二項邏輯迴歸模型是一種二分類模型，儘管它叫“迴歸”。 模型如下： P(Y=1|x)=e(w⋅x+b)1+e(

   Logistic Regression(邏輯斯特迴歸)

   Logistic Regression實際上是基於Linear Regression的，與Linear Regression的不同在於輸出增加了一個非線性對映，即應用邏輯斯特函式將回歸結果對映到0到1(能夠將負無窮到正無窮對映到0-1的函式有很多，但是Logistic函式

   Logistic Regression 邏輯回歸

   維度 擬合 我們 del ble sca con douban label 問題描述 收集到某一地區的房子面積和房價的數據（x, y）42組,對於一套已知面積的房子預測其房價？ 由房價數據可視化圖可以看出，可以使用一條直線擬合房價。通過這種假設得到的預測值和真實值比較接

   Logistic Regression邏輯回歸

   一個 div 新的 損失函數 OS gre gist log 轉化 邏輯回歸 針對二分類問題，若X是特征集合，Y是類別標簽（0，1），假設Y的取值服從伯努利分布，即 \(P(Y=0|X)=1-p\) \(P(Y=1|X)=p\) 再假設p是可以由已知的特征集合X預測的，令(

   coursera 機器學習 logistic regression 邏輯回歸的項目

   sta expected face useful regular screen see div eth github : https://github.com/twomeng/logistic-regression- ex1. m 1 %% Machine L

   清華AI自強計劃作業2實驗—邏輯迴歸模型

   問題： 執行模型輸出loss值為NAN,訓練200次後未出現線性模型 nan nan的資料型別為float, not a number 的縮寫。python中判斷是否為nan型別的方法，使用math庫中的*isnan()*函式判斷： from math import

   tensorflow構造邏輯迴歸模型

   import numpy as np import tensorflow as tf import matplotlib.pyplot as plt import input_data mnist = input_data.read_data_sets('data/', one_hot=True)