1.背景

          決策書演算法是一種逼近離散數值的分類演算法，思路比較簡單，而且準確率較高。國際權威的學術組織，資料探勘國際會議ICDM （the IEEE International Conference on Data Mining）在2006年12月評選出了資料探勘領域的十大經典演算法中，C4.5演算法排名第一。C4.5演算法是機器學習演算法中的一種分類決策樹演算法,其核心演算法是ID3演算法。

          演算法的主要思想就是將資料集按照特徵對目標指數的影響由高到低排列。行成一個二叉樹序列，進行分類，如下圖所示。

         現在的問題關鍵就是，當我們有很多特徵值時，哪些特徵值作為父類寫在二叉樹的上面的節點，哪下寫在下面。我們可以直觀的看出上面的特徵值節點應該是對目標指數影響較大的一些特徵值。那麼如何來比較哪些特徵值對目標指數影響較大呢。這裡引出一個概念，就是資訊熵。

        資訊理論的鼻祖之一Claude E. Shannon把資訊（熵）定義為離散隨機事件的出現概率。說白了就是資訊熵的值越大就表明這個資訊集越混亂。

        資訊熵的計算公式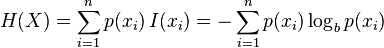，（建議去wiki學習一下）

        這裡我們通過計算目標指數的熵和特徵值得熵的差，也就是熵的增益來確定哪些特徵值對於目標指數的影響最大。

2.資料集

                    

3.程式碼

（1）第一部分-計算熵

def calcShannonEnt(dataSet):
    numEntries=len(dataSet)
    
    labelCounts={}

    for featVec in dataSet:
        currentLabel=featVec[-1]
       
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel]=0        
        labelCounts[currentLabel]+=1
    shannonEnt=0.0
    
    for key in labelCounts:
         
         prob =float(labelCounts[key])/numEntries        
         shannonEnt-=prob*math.log(prob,2)

    return shannonEnt      
 

     （2）第二部分-分割資料

def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     #chop out axis used for splitting            
            reducedFeatVec.extend(featVec[axis+1:])      
            retDataSet.append(reducedFeatVec)          
    return retDataSet

   （3）第三部分-找出資訊熵增益最大的特徵值

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      #the last column is used for the labels
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):        #iterate over all the features
        featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
       
        uniqueVals = set(featList)       #get a set of unique values
        
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy     #calculate the info gain; ie reduction in entropy
        
        if (infoGain > bestInfoGain):       #compare this to the best gain so far
            bestInfoGain = infoGain         #if better than current best, set to best
            bestFeature = i
    return bestFeature                      #returns an integer

4.程式碼下載