不只是噪聲,更是數學美 ---淺談Perlin Noise
阿新 • • 發佈:2018-12-30
首先說明為什麼這篇部落格叫這個題目,我剛剛開始學習Perlin Noise是從知乎上的一篇文章入門的,作者的題目是不只是噪聲,我覺得很有韻味,就借鑑過來。這是連結:https://zhuanlan.zhihu.com/p/22337544
一. 背景
Perlin Noise,譯作柏林噪聲,是指Ken Perlin發明的噪聲演算法。Ken Perlin早在1983年就提出了Perlin noise,當時他正在參與制作迪士尼的動畫電影《電子世界爭霸戰》(TRON),但是他不滿足於當時計算機產生的那種非常不自然的紋理效果,因此提出了Perlin噪聲。隨後,他在1984年的SIGGRAPH Course上做了名為Advanced Image Synthesis1的課程演講,並在SIGGRAPH 1985上發表了他的論文[Perlin K. An image synthesizer[J]. ACM Siggraph Computer Graphics, 1985, 19(3): 287-296.](Perlin K. An image synthesizer[J]. ACM Siggraph Computer Graphics, 1985, 19(3): 287-296.)。由於Perlin噪聲的演算法簡單,被迅速應用到各種商業軟體中。後來Perlin繼續研究程式紋理的生成,並和他的一名學生又在SIGGRAPH 1989上發表了一篇文章[Perlin K, Hoffert E M. Hypertexture[C]//ACM SIGGRAPH Computer Graphics. ACM, 1989, 23(3): 253-262](Perlin K, Hoffert E M. Hypertexture[C]//ACM SIGGRAPH Computer Graphics. ACM, 1989, 23(3): 253-262),提出了超級紋理(hypertexture)。他們使用噪聲+fbm+ray marching實現了各種有趣的效果。到1990年,已經有大量公司在他們的產品中使用了Perlin噪聲。在1999年的GDCHardCore大會上,Ken Perlin做了名為Making Noise的演講[Perlin K. Making noise[C]//Proc. of the Game Developer Conference. 1999.](Perlin K. Making noise[C]//Proc. of the Game Developer Conference. 1999.),系統地介紹了Perlin噪聲的發展、實現細節和應用。在2002年他對原有的柏林噪聲演算法做了改進,並發表了論文ImprovingNoise。
Prelin由於出色的工作,獲得了奧斯卡科技成果獎(奧斯卡是電影業的諾貝爾獎,靠著一個演算法單槍匹馬獲得這個獎勵,Perlin確實厲害)。
二. 分類
看了很多部落格,博主都沒有把分形噪聲和Simplex噪聲歸為柏林噪聲。但是我覺得這樣不對,因為分形噪聲和Simplex都是柏林先後提出來的,所以我把這2個和原始的柏林噪聲一起歸為柏林噪聲,在後面都做介紹。事實上,維基百科也是這樣做的,將這3個噪聲全部歸為柏林噪聲。https://zh.wikipedia.org/wiki/Perlin%E5%99%AA%E5%A3%B0
根據wiki,由程式產生噪聲的方法大致可以分為兩類:
| 類別 | 名稱 |
|---|---|
| 基於晶格的方法(Lattice based) | 又可細分為兩種: 第一種是梯度噪聲(Gradient noise),包括Perlin噪聲, Simplex噪聲,Wavelet噪聲等; 第二種是Value噪聲(Value noise)。 |
| 基於點的方法(Point based) | Worley噪聲 |
從這個表格中,我們可以看到柏林噪聲的產生是基於晶格的方法,從後面的介紹中相信一定會對”晶格”這個名字有一個深刻的理解。
下面貼出幾張圖片,先對這柏林噪聲中的3種形式有一個直觀的印象。

隨機噪聲

原始柏林噪聲

分形噪聲

Simplex噪聲
從這4張圖片中我們可以大概看出不同噪聲的一些端倪,隨機噪聲就像黑白電視一樣,雜亂無章。原始的柏林噪聲中包含有隨機的成分,但是相互之間又有關聯,畫素點之間是平滑的進行變化,而不是像白噪聲那麼尖銳。分形噪聲就像我們在計算機圖形學中學的分形樹,簡單的細節不斷的重複,最後生成一個複雜的圖形。
下面對白噪聲,原始的柏林噪聲,分形噪聲,Simplex噪聲的原理一一解釋。
三. 白噪聲
噪聲的基礎是隨機數,如果給螢幕上的每個畫素點賦予一個0和1之間的隨機數來表示畫素點的亮度,就會得到一幅雜亂無章的圖片,就像我們小時候家裡的電視在下雨天突然沒有訊號後螢幕上呈現的影象。從程式設計師的角度來看白噪聲,我們無非就是引入一些隨機變數到程式,給定一個輸入(比如種子),程式給出一個輸出。在C中,rand.h中對rand函式進行了宣告,我們只要在自己的程式中引入這個標頭檔案就行。不過這裡生成的隨機數是偽隨機數,我們可以採用時間來作為種子。C++中也有實現了隨機數的庫,和C類似,畢竟是C的延伸和拓展。Python的第三方模組random對隨機數的實現更加強大,因為在很多機器學習方法中需要用的隨機數。U3D中通過Ramdom.Range()l來實現隨機數的生成。基本的程式框架如下:(以Python為例)
import random
random.seed()
random.random()
我們從上面的程式碼生成隨機數的過程中可以看出,這樣產生的噪聲非常不自然,聽起來不自然,看起來也不好看。這學期學了訊號與系統,不妨從訊號的角度來考慮這個問題,一幅隨機噪聲的影象的功率譜密度在整個頻域內均勻分佈, 所有頻率具有相同能量密度。也就是說,白噪聲是指在較寬的頻率範圍內,各等頻寬的頻帶所含的噪聲能量相等。白噪聲就像全綵色白顏色的光頻。
白噪聲雖然很好模擬,但是自身具有不可修復的缺點。觀察現實生活中的自然噪聲,它們不會長成上面這個樣子。例如木頭紋理、山脈起伏,它們的形狀大多是趨於分形狀(fractal)的,即包含了不同程度的細節。比如地形,它有起伏很大的山脈,也有起伏稍小的山丘,也有細節非常多的石子等,這些不同程度的細節共同組成了一個自然的地形表面。這些隨機的成分並不是完全獨立的,他們之間有一定的關聯。採用微積分裡面的說法,就是畫素點之間變化是連續的,並沒有發生跳變。很顯然,白噪聲沒有做到這一點。
四. 原始的柏林噪聲
從上一部分的討論中,我們可以看到白噪聲的缺點,原始柏林噪聲的提出正是針對這一缺點。在大二學的數值分析中,我們學了很多插值方法,用來平滑變化趨勢,這種方法在上學期X老師教的數字影象處理中處處可見。原始柏林噪聲的原理就是基於插值的方法,平滑變化趨勢,這讓噪聲可以更好地模擬自然世界的萬物。下面討論一維,二維,三維柏林噪聲的原理及其實現。
1. 一維柏林噪聲
首先,在X軸上每個整數座標隨機生成一個數(範圍為-1~1),我們稱這個數為Gradient,譯為梯度或者斜率。然後我們對相鄰兩個整數之間使用梯度進行插值計算,使得相鄰兩點之間平滑過渡。平滑度取決於所選用的插值函式,老版的柏林噪聲使用f(t)=3*t*t-2*t*t*t,改進後的柏林噪聲使用f(t)=t*t*t*(t*(t*6-15)+10)。如圖所示:

上圖來自於KenPerlin的Simplex Noise論文,論文中提到了經典的柏林噪聲定義。
在這裡,需要注意一個問題,上面說的梯度和我們在微積分裡面學的梯度並不是一回事。在多元微分學中,梯度的定義是函式對各個座標軸的偏導數,只要空間中的位置確定,函式在這一點的梯度就已經確定。梯度的數學意義是空間沿著梯度的方向變化最快。這裡的梯度是隨機生成的,至於如何生成,這個關鍵問題在後面單獨討論。(起初把這裡的梯度和微積分裡的梯度等同,結果遲遲沒有理解柏林噪聲的原理)。
2. 二維柏林噪聲
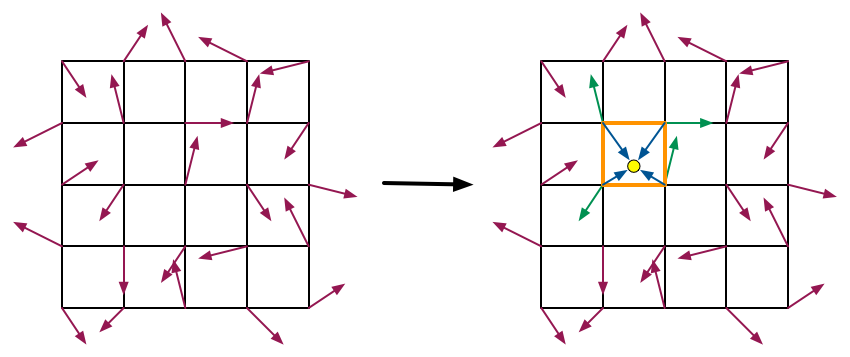
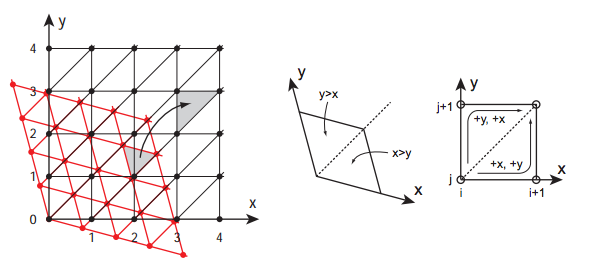
對於二維來說我們可以獲取點P(x, y)最近的四個整數點ABCD,ABCD四個點的座標分別為A(i, j)、B(i+1, j)、C(i, j+1)、D(i+1, j+1),隨後獲取ABCD四點的二維梯度值G(A)、G(B)、G(C)、G(D),並且算出ABCD到P點的向量AP、BP、CP以及DP。如下圖所示:

紅色箭頭表示該點處的梯度值,綠色箭頭表示該點到P點的向量。接著,將G(A)與AP進行點乘,計算出A點對於P點的梯度貢獻值,然後分別算出其餘三個點對P點的梯度貢獻值,最後將(u, v)代入插值函式中算出P點的最終噪聲值。
3. 三維柏林噪聲
將以上討論類推到三維的柏林噪聲,則需要算出八個頂點的梯度貢獻值,然後進行插值計算。在後來的改進演算法中,取的是立方體12條邊的中點。這樣處理來保證各個方向之間的不關聯性,帶來的是計算量的提高,增加了接近一半的計算量。

在一篇部落格中,博主給出了詳細的計算過程,想了解詳細的過程可以看http://www.twinklingstar.cn/2015/2581/classical-perlin-noise/。
4. 隨機梯度的選取
對於隨機梯度的選取,柏林採用了這樣一種方法:預先生成256個偽隨機的梯度值(以及二維和三維的梯度向量)儲存在G1[256]、G2[256][2]]以及G3[256][3]中,然後對於一維柏林噪聲來說,我們可以直接去取G1[]陣列中的梯度值使用,對於二維或者三維,預先又生成了一個排列P[256],將0~255的下標隨機存放在P陣列中,然後通過下面公式來取到隨機的梯度值:
G2[P[x] + y] ——二維
G3[P[P[x] + y] +z] ——三維
以上就完成了隨機取梯度值的演算法。
這裡還要提一下在Improved Noise論文中柏林對於三維柏林噪聲的改進。在論文中柏林的第一個改進就是插值函式的改進,也就是我們上面提到過的f(t)=t*t*t*(t*(t*6-15)+10),它使得插值出來的噪聲值更平滑了,特別是在三維中。


左邊是以前的插值函式計算的結果,右邊是改進後的插值函式計算的結果,不難看出,右邊的效果提高了不少。
對於上面的過程,如果感覺不很懂,建議直接看柏林的論文。http://mrl.nyu.edu/~perlin/paper445.pdf
5. 實現
Perlin噪聲實現比較簡單的,在1983年的計算機上實現的演算法也不允許對計算量、記憶體有多大的要求。概括來說,Perlin噪聲的實現需要三個步驟:
# a. 定義一個晶格結構,每個晶格的頂點有一個“偽隨機”的梯度向量(其實就是個向量啦)。對於二維的Perlin噪聲來說,晶格結構就是一個平面網格,三維的就是一個立方體網格。
# b. 輸入一個點(二維的話就是二維座標,三維就是三維座標,n維的就是n個座標),我們找到和它相鄰的那些晶格頂點(二維下有4個,三維下有8個,n維下有2n X 2n個),計算該點到各個晶格頂點的距離向量,再分別與頂點上的梯度向量做點乘,得到2n X 2n個點乘結果。
# c. 使用緩和曲線(ease curves)來計算它們的權重和。在原始的Perlin噪聲實現中,緩和曲線是s(t)=3t^2−2t^3 s(t)=3t^2−2t^3,在2002年的論文中[Perlin K. Improving noise[C]//ACM Transactions on Graphics (TOG). ACM, 2002, 21(3): 681-682](Perlin K. Improving noise[C]//ACM Transactions on Graphics (TOG). ACM, 2002, 21(3): 681-682),Perlin改進為s(t)=6t^5−15t^4+10t^3 s(t)=6t^5−15t^4+10t^3。這裡簡單解釋一下,為什麼不直接使用s(t)=t,即線性插值。直接使用的線性插值的話,它的一階導在晶格頂點處(即t = 0或t = 1)不為0,會造成明顯的不連續性。s(t)=3t^2−2t^3 s(t)=3t^2−2t^3在一階導滿足連續性,s(t)=6t^5−15t^4+10t^3 s(t)=6t^5−15t^4+10t^3在二階導上仍然滿足連續性。
以二維為例,下面的圖可以展示第一步和第二步的過程。
6. 演算法時間複雜度分析
Perlin噪聲演算法的時間複雜度為O(2^n)(n是維數),2^n其實就是每個晶格的頂點個數。可見對於輸入點需要進行指數級別的點乘操作。因此,隨著維數的增大,例如計算三維四維的Perlin噪聲,時間會迅速增加。為了解決這個問題,Perlin在2002年提出了優化後的一種噪聲——Simplex噪聲,這種噪聲的複雜度是O(n^2),在高緯度上時間優化明顯,這樣的時間複雜度類似於based-compared sort,時間複雜度顯著下降。
對於演算法在時間複雜度上的提高,我們可以把柏林噪聲的實現演算法當成斐波那契數列的遞迴實現,把Simplex演算法當成一般的氣泡排序。這2個實驗我們都做過,執行時間應該都有直觀的印象。
五. 分形噪聲
分形噪聲可以用來模擬自然界的自相似過程,包括海岸線,地形,海浪等。分形噪聲的原理是利用Perlin噪聲頻率受限的特性,通過不斷疊加更高頻率的perlin噪聲達到自相似的效果。(定義來自維基百科https://zh.wikipedia.org/wiki/Perlin%E5%99%AA%E5%A3%B0)
關於分形噪聲的詳細介紹可以參看這篇部落格。https://blog.csdn.net/syfolen/article/details/75051066
1. 一維分形噪聲
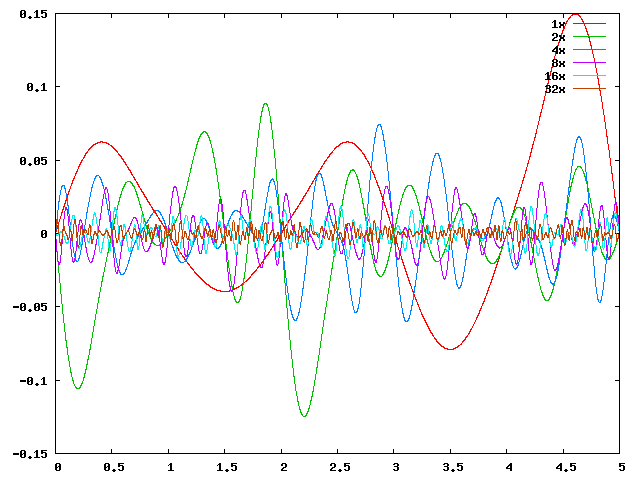
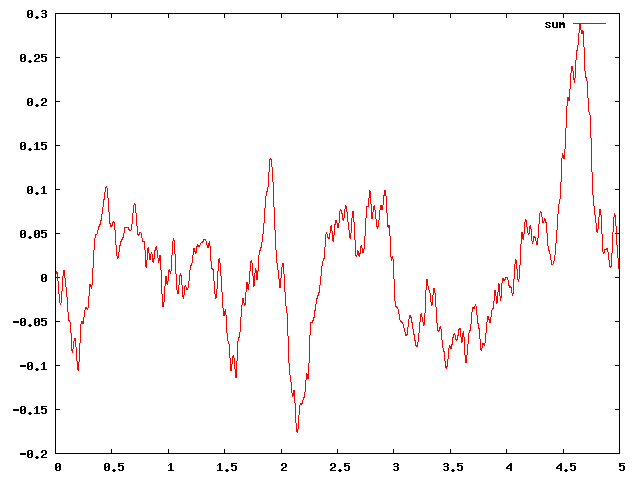
在一維的情況下,設噪聲函式為noise(x),則通過 noise(2x), noise(4x)等就可以構造更高頻率的噪聲。下圖第一張圖是一維Perlin噪聲頻率頻率在不斷倍增,振幅不斷倍減的情況,第二張圖是第一張圖中這些函式求和的影象。
不同頻率下的分形噪聲
合併後的分形噪聲
上面第二張影象是自相似的,將它放大會得到和原圖相似的效果。從數學上描述分形噪聲,則是:

分形噪聲有時也被稱作1/f噪聲
2. 二維分形噪聲
對於二維的情況,可以使用類似的方法進行分形和運算,產生的效果類似於雲層,如下圖所示。




# 上圖依次為:二維Simplex噪聲原函式, 二維Simplex噪聲疊加2倍頻, 二維Simplex噪聲疊加到4倍頻, 二維Simplex噪聲疊加到128倍頻。
對分形和函式進行一些小修改可以模擬各種複雜效果,具體詳見如下連結https://zh.wikipedia.org/wiki/Perlin%E5%99%AA%E5%A3%B0
六. Simplex噪聲
在2001年SIGGRAPH Course上,Ken Perlin進行了一次演講,他介紹了對Perlin噪聲的一個改進版噪聲——Simplex噪聲。給出Perlin原版的Course Note連結https://www.csee.umbc.edu/~olano/s2002c36/ch02.pdf。,Simplex噪聲的計算複雜度為O(n^2),優於Perlin噪聲的O(2^n)。而且在效果上,Simplex噪聲也克服了經典的Perlin噪聲在某些視覺問題。但Simplex噪聲很難理解,我看了好幾天也理解了一個大概,因此這一部分寫的忐忐忑忑,錯誤在所難免。
Simplex 噪聲使用 6t^5 - 15t^4 + 10t^3 作為插值函式,杜絕了導數中的線性部分。另外,Simplex 噪聲演算法有效地降低了插值次數。
1. 實現
二維經典Perlin噪聲將二維空間用正方形填充,用四個頂點進行3次插值,而Simplex噪聲將二維空間用等邊三角形填充,使用三個頂點進行插值。三維經典Perlin噪聲將三維空間用立方體進行填充,使用8個頂點進行7次插值,三維Simplex噪聲使用正四面體填充空間,用4個頂點進行插值。對於更高維(N維)的情況,經典Perlin噪聲將空間用超立方體填充,頂點數目是 2^N,而Simplex噪聲使用高維正三角形(稱為Simplex)進行填充,頂點數目為 N+1。Simplex噪聲插值次數隨維數增長線性增長。
對於二維的情況,使用正三角形填充空間使得直接判斷某點落在哪個正三角形中,計算該三角形的頂點位置變得複雜。在實現上通常通過座標變換將正三角形對映成直角三角形。使用該方法進行變換可以使用和經典Perlin噪聲相同的方法對頂點進行求值.http://staffwww.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf
網上一篇部落格對Simplex噪聲的實現進行了詳細的介紹,下面對其進行總結。先給出部落格地址,看不懂下面的總結可以直接去看部落格,部落格講的比較詳細。https://blog.csdn.net/candycat1992/article/details/50346469
Simplex噪聲和Perlin噪聲在實現上的區別是他的晶格不是方形,而是單形。單形就是N維空間中最簡單緊湊的多邊形。二維空間單形就是等邊三角形,三維空間就是四面體。單形的頂點數目遠少於N方體,因此計算梯度噪聲時可以大大減少需要計算的頂點權重數目。
以二維空間為例:
每個頂點的噪聲貢獻度為:(r^2−|dist|^2)^4×dot(dist,grad)dist。dist 是輸入點到該頂點的距離向量,gradgrad是該點儲存的偽隨機梯度向量,r2r2的取值是0.5或0.6。取0.5時可以保證沒有不連續的間斷點,在連續性並不那麼明顯時可以取0.6得到更好的視覺效果。
上面的實現中我們始終忽略了一個問題,就是如何找到輸入點所在的單形?下面對這個問題進行探討。
2.尋找單體
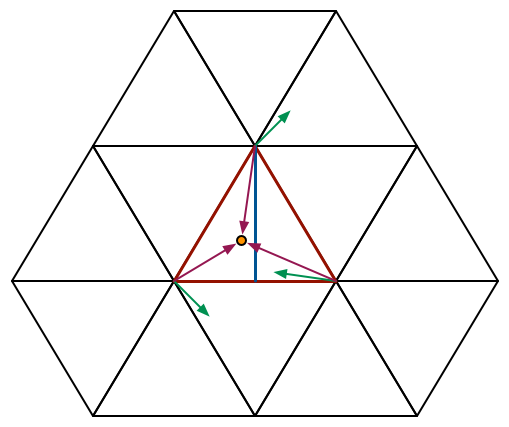
把單形進行座標偏斜(skewing),把平鋪空間的單形變成一個新的網格結構,這個網格結構是由超立方體組成的,而每個超立方體又由一定數量的單形構成。
之前提到的單形網格如上圖中的紅色網格所示,它們有一些等邊三角形組成(注意到這些等邊三角形是沿空間對角線排列的)。經過座標傾斜後,它們變成了後面的黑色網格,這些網格由正方形組成,每個正方形是由之前兩個等邊三角形變形而來的三角形組成。這個把N維空間下的單形網格變形成新網格的公式如下:
x′=x+(x+y+…)⋅K1
y′=y+(x+y+…)⋅K1
其中,K1=(sqrt(n + 1) - 1) / n.
接下來就很難懂了,我可能也講不清楚,如果對這方面感興趣可以去參看上面給出的部落格連結。
3. Simplex噪聲和經典Perlin噪聲的應用
Perlin噪聲可以用來模擬自然界中的噪聲現象。由於它的連續性,如果將二維噪聲中的一個軸作為時間軸,得到的就是一個連續變化的一維函式。同樣的也可以得到連續變化的二維影象。該噪聲可以用來模擬人體的隨機運動,螞蟻行進的線路等。另外,還可以通過計算分形和模擬雲朵,火焰等非常複雜的紋理。
Perlin噪聲對各個點的計算是相互獨立的,因此非常適合使用圖形處理器進行計算。OpenGL在GLSL中定義了一維至四維的噪聲函式noise1、noise2、noise3、noise4,在該規範中噪聲的性質與上述Perlin提出的性質相同。在Mesa 3D實現中,這一組函式是使用Simplex演算法實現的。在硬體的實現中,噪聲的生成可以達到實時效果。

使用Simplex噪聲模擬木紋
七. Unity中Perlin Noise的實現
首先給出出處:http://flafla2.github.io/2014/08/09/perlinnoise.html
下面介紹Simplex的演算法實現.
public double perlin(double x, double y, double z);
函式接收x,y,z三個座標分量作為輸入,並返回0.0~1.0的double值作為輸出。那我們應該怎麼處理輸入值?首先,我們取3個輸入值x,y,z的小數點部分,就可以表示為單元空間裡的一個點了。為了方便講解,我們將問題降維到2維空間來討論(原理是一樣的),下圖是該點在2維空間上的表示:
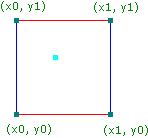
小藍點代表輸入值在單元正方形裡的空間座標,其他4個點則是單元正方形的各頂點
接著,我們給4個頂點(在3維空間則是8個頂點)各自生成一個偽隨機的梯度向量。梯度向量代表該頂點相對單元正方形內某點的影響是正向還是反向的(向量指向方向為正向,相反方向為反向)。而偽隨機是指,對於任意組相同的輸入,必定得到相同的輸出。因此,雖然每個頂點生成的梯度向量看似隨機,實際上並不是。這保證了在生成函式不變的情況下,每個座標的梯度向量都是確定不變的。
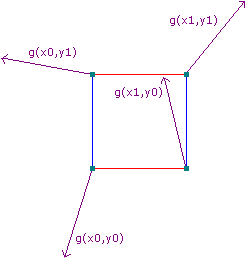
各頂點上的梯度向量隨機選取結果
上圖所示的梯度向量並不是完全準確的。在本文所介紹的改進版柏林噪聲中,這些梯度向量並不是完全隨機的,而是由單位正方體(3維)的中心點指向各條邊中點的12個向量:(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0), (1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1), (0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1),具體原因參見:http://mrl.nyu.edu/~perlin/paper445.pdf
接著,我們需要求出另外4個距離向量(在3維空間則是8個),它們分別從各頂點指向輸入點(藍色點)。下面有個2維空間下的例子:
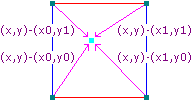
各個距離向量
對每個頂點的梯度向量和距離向量做點積運算,就可以得出每個頂點的影響值:grad.x * dist.x + grad.y * dist.y + grad.z * dist.z
點積可以理解為向量a在向量b上的投影,當距離向量在梯度向量上的投影為同方向,點積結果為正數;當距離向量在梯度向量上的投影為反方向,點積結果為負數。因此,通過兩向量點積,我們就知道該頂點的影響值是正還是負的。不難看出,頂點的梯度向量直接決定了這一點。下面通過一副彩色圖,直觀地看下各頂點的影響值:
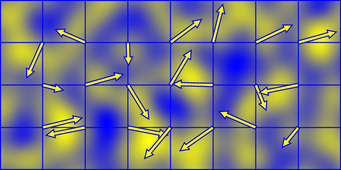
2D柏林噪聲的影響值
下一步,我們需要對4個頂點的影響值做插值,求得加權平均值(在3維空間則是8個)。演算法非常簡單(2維空間下的解法):
// Below are 4 influence values in the arrangement:
// [g1] | [g2]
// -----------
// [g3] | [g4]
int g1, g2, g3, g4;
int u, v; // These coordinates are the location of the input coordinate in its unit square.
// For example a value of (0.5,0.5) is in the exact center of its unit square.
int x1 = lerp(g1,g2,u);
int x2 = lerp(g3,h4,u);
int average = lerp(x1,x2,v);
如果直接使用上述程式碼,由於是採用lerp線性插值計算得出的值,雖然執行效率高,但噪聲效果不好,看起來會不自然。我們需要採用一種更為平滑,非線性的插值函式:fade函式,通常也被稱為ease curve。

ease curve
ease curve的值會用來計算前面程式碼裡的u和v,這樣插值變化不再是單調的線性變化,而是這樣一個過程:初始變化慢,中間變化快,結尾變化又慢下來(也就是在當數值趨近於整數時,變化變慢)。這個用於改善柏林噪聲演算法的fade函式可以表示為以下數學形式:

基本上,這就是整個柏林噪聲演算法的原理了!
程式碼實現
1. 準備工作
第一步,我們需要先宣告一個排列表(permutation table),或者直接縮寫為p[]陣列就行了。陣列長度為256,分別隨機、無重複地存放了0-255這些數值。為了避免快取溢位,我們再重複填充一次陣列的值,所以陣列最終長度為512:
private static readonly int[] permutation = { 151,160,137,91,90,15, // Hash lookup table as defined by Ken Perlin. This is a randomly
131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23, // arranged array of all numbers from 0-255 inclusive.
190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
};
private static readonly int[] p; // Doubled permutation to avoid overflow
static Perlin() {
p = new int[512];
for(int x=0;x<512;x++) {
p[x] = permutation[x%256];
}
}
p[]陣列會在演算法後續的雜湊計算中使用到,用於確定一組輸入最終挑選哪個梯度向量(從前面所列出的12個梯度向量中挑選)。後續程式碼會詳細展示p[]陣列的用法。
接著,我們開始宣告柏林噪聲函式:
public double perlin(double x, double y, double z) {
if(repeat > 0) { // If we have any repeat on, change the coordinates to their "local" repetitions
x = x%repeat;
y = y%repeat;
z = z%repeat;
}
int xi = (int)x & 255; // Calculate the "unit cube" that the point asked will be located in
int yi = (int)y & 255; // The left bound is ( |_x_|,|_y_|,|_z_| ) and the right bound is that
int zi = (int)z & 255; // plus 1. Next we calculate the location (from 0.0 to 1.0) in that cube.
double xf = x-(int)x;
double yf = y-(int)y;
double zf = z-(int)z;
// ...
}
上面的程式碼很直觀。首先,對輸入座標使用求餘運算子%,求出[0,repeat)範圍內的餘數。宣告xi, yi, zi三個變數。它們代表了輸入座標落在了哪個單元正方形裡。我們還要限制座標在0,255這個範圍內,避免訪問陣列p[]時,出現數組越界錯誤。這也產生了一個副作用:柏林噪聲每隔256個整數就會再次重複。但這不是太大的問題,因為演算法不僅能處理整數,還能處理小數。最後,我們通過xf, yf, zf三個變數(也就是x,y,z的小數部分值),確定了輸入座標在單元正方體裡的空間位置(就是前面所示的小藍點)。
2. Fade函式
public static double fade(double t) {
// Fade function as defined by Ken Perlin. This eases coordinate values
// so that they will ease towards integral values. This ends up smoothing
// the final output.
return t * t * t * (t * (t * 6 - 15) + 10); // 6t^5 - 15t^4 + 10t^3
}
public double perlin(double x, double y, double z) {
// ...
double u = fade(xf);
double v = fade(yf);
double w = fade(zf);
// ...
}
3. 雜湊函式
public double perlin(double x, double y, double z) {
// ...
int aaa, aba, aab, abb, baa, bba, bab, bbb;
aaa = p[p[p[ xi ]+ yi ]+ zi ];
aba = p[p[p[ xi ]+inc(yi)]+ zi ];
aab = p[p[p[ xi ]+ yi ]+inc(zi)];
abb = p[p[p[ xi ]+inc(yi)]+inc(zi)];
baa = p[p[p[inc(xi)]+ yi ]+ zi ];
bba = p[p[p[inc(xi)]+inc(yi)]+ zi ];
bab = p[p[p[inc(xi)]+ yi ]+inc(zi)];
bbb = p[p[p[inc(xi)]+inc(yi)]+inc(zi)];
// ...
}
public int inc(int num) {
num++;
if (repeat > 0) num %= repeat;
return num;
}
程式碼的雜湊函式,對包圍著輸入座標(小藍點)的周圍8個單元正方形的索引座標進行了雜湊計算。inc()函式用於將輸入值增加1,同時保證範圍在[0,repeat)內。如果不需要噪聲重複,inc()函式可以簡化成單純將輸入值增加1。由於雜湊結果值是從p[]陣列中得到的,所以雜湊函式的返回值範圍限定在0,255內。
4. 梯度函式
grad()函式的作用在於計算隨機選取的梯度向量以及頂點位置向量的點積。Ken Perlin巧妙地使用了位翻轉(bit-flipping)技巧來實現:
public static double grad(int hash, double x, double y, double z) {
int h = hash & 15; // Take the hashed value and take the first 4 bits of it (15 == 0b1111)
double u = h < 8 /* 0b1000 */ ? x : y; // If the most significant bit (MSB) of the hash is 0 then set u = x. Otherwise y.
double v; // In Ken Perlin's original implementation this was another conditional operator (?:). I
// expanded it for readability.
if(h < 4 /* 0b0100 */) // If the first and second significant bits are 0 set v = y
v = y;
else if(h == 12 /* 0b1100 */ || h == 14 /* 0b1110*/) // If the first and second significant bits are 1 set v = x
v = x;
else // If the first and second significant bits are not equal (0/1, 1/0) set v = z
v = z;
return ((h&1) == 0 ? u : -u)+((h&2) == 0 ? v : -v); // Use the last 2 bits to decide if u and v are positive or negative. Then return their addition.
}
下面程式碼則是以另一種令人容易理解的方式完成了這個任務(而且在很多語言版本的執行效率都優於前面一種):
// Source: http://riven8192.blogspot.com/2010/08/calculate-perlinnoise-twice-as-fast.html
public static double grad(int hash, double x, double y, double z)
{
switch(hash & 0xF)
{
case 0x0: return x + y;
case 0x1: return -x + y;
case 0x2: return x - y;
case 0x3: return -x - y;
case 0x4: return x + z;
case 0x5: return -x + z;
case 0x6: return x - z;
case 0x7: return -x - z;
case 0x8: return y + z;
case 0x9: return -y + z;
case 0xA: return y - z;
case 0xB: return -y - z;
case 0xC: return y + x;
case 0xD: return -y + z;
case 0xE: return y - x;
case 0xF: return -y - z;
default: return 0; // never happens
}
}
上面的兩種實現並沒有實質差別。他們都是從以下12個向量裡隨機挑選一個作為梯度向量:(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0), (1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1), (0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1).隨機挑選結果其實取決於前一步所計算得出的雜湊值(grad()函式的第一個引數)。後面3個引數則代表由輸入點指向頂點的距離向量(最終拿來與梯度向量進行點積)。
5. 插值整合
經過前面的幾步計算,我們得出了8個頂點的影響值,並將它們進行平滑插值,得出了最終結果:
public double perlin(double x, double y, double z) {
// ...
double x1, x2, y1, y2;
x1 = lerp( grad (aaa, xf , yf , zf), // The gradient function calculates the dot product between a pseudorandom
grad (baa, xf-1, yf , zf), // gradient vector and the vector from the input coordinate to the 8
u); // surrounding points in its unit cube.
x2 = lerp( grad (aba, xf , yf-1, zf), // This is all then lerped together as a sort of weighted average based on the faded (u,v,w)
grad (bba, xf-1, yf-1, zf), // values we made earlier.
u);
y1 = lerp(x1, x2, v);
x1 = lerp( grad (aab, xf , yf , zf-1),
grad (bab, xf-1, yf , zf-1),
u);
x2 = lerp( grad (abb, xf , yf-1, zf-1),
grad (bbb, xf-1, yf-1, zf-1),
u);
y2 = lerp (x1, x2, v);
return (lerp (y1, y2, w)+1)/2; // For convenience we bind the result to 0 - 1 (theoretical min/max before is [-1, 1])
}
// Linear Interpolate
public static double lerp(double a, double b, double x) {
return a + x * (b - a);
}
6. 利用倍頻實現更自然的噪聲
最後讓我們再思考下,除了前面所講的計算,還有其他辦法可以令噪聲結果更加自然嗎?雖然柏林噪聲演算法一定程度上模擬了自然噪聲,但仍沒有完全表現出自然噪聲的不規律性。舉個現例項子,現實地形會有大段連綿、高聳的山地,也會有丘陵和蝕坑,更小點的有大塊岩石,甚至更小的鵝卵石塊,這都屬於地形的一部分。那如何讓柏林噪聲演算法模擬出這樣的自然噪聲特性,解決方法也很簡單:我們可以使用不同的頻率(frequencies)和振幅(amplitudes)引數進行多幾次柏林噪聲計算,然後將結果疊加在一起。頻率是指取樣資料的間隔,振幅是指返回值的幅度範圍。
public double OctavePerlin(double x, double y, double z, int octaves, double persistence) {
double total = 0;
double frequency = 1;
double amplitude = 1;
double maxValue = 0; // Used for normalizing result to 0.0 - 1.0
for(int i=0;i<octaves;i++) {
total += perlin(x * frequency, y * frequency, z * frequency) * amplitude;
maxValue += amplitude;
amplitude *= persistence;
frequency *= 2;
}
return total/maxValue;
}