資料結構——圖的連通性(生成樹、最小生成樹、生成森林)
阿新 • • 發佈:2018-12-26
1、求圖的生成樹(或生成森林)
生成樹:是一個極小連通子圖,它含有圖中全部n個頂點,但只有n-1條邊。
生成森林: 由若干棵生成樹組成,含全部頂點,但構成這些樹的邊是最少的。
深度優先搜尋生成樹: 由深度優先搜尋得到的生成樹
廣度優先搜尋生成樹: 由廣度優先搜尋得到的生成樹
若對連通圖進行遍歷,得到的是圖的生成樹
若對非連通圖進行遍歷,得到的是 圖的生成森林
例1:畫出下圖的生成森林(或極小連通子圖)
 求解步驟:
求解步驟:
Step1:先求出鄰接矩陣或鄰接表;
Step2:寫出DFS或BFS結果序列;
Step3:畫出對應子圖或生成森林。
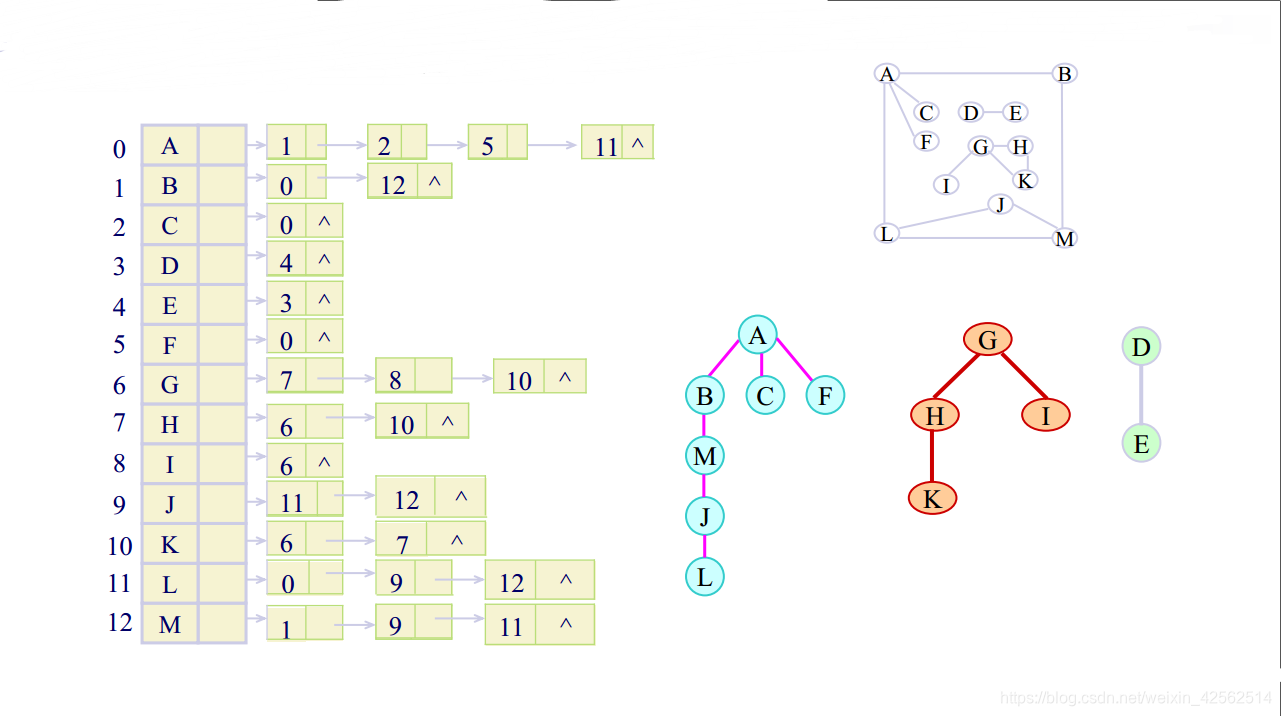
2、求圖的最小生成樹
n個頂點的生成樹很多,需要從中選一棵代價最小的生成樹,即該樹各邊的代價之和最小。此樹便稱為最小生成樹MST。
目標: 在網路的多個生成樹中,尋找一個各邊權值之和最小的生成樹。
構造最小生成樹的準則
- 必須只使用該網路中的邊來構造最小生成樹;
- 必須使用且僅使用n-1條邊來連線網路中的n個頂點;
- 不能使用產生迴路的邊。
(1)Prim(普里姆)演算法
基本思想:在圖中任取一個頂點K作為開始點,令U={k}, V=W-U,其中W為圖中所有頂點集,然後找一個頂點在U中,另一個頂點在V中的邊中最短的一條,找到後,將該邊作為最小生成樹的邊儲存起來,並將該邊頂點全部加入U集合中,並從V中刪去這些頂點,然後再重複此過程,直到V為空集止。
具體實現過程:

(1)Kruskal(克魯斯卡爾)演算法
基本思想:將圖中所有邊按權值遞增順序排列,依次選取權值較小的邊,但要求後面選取的邊不能與前面選取的邊構成迴路,若構成迴路,則放棄該條邊,再去選後面權值較大的邊, n個頂點的圖中,選夠n-1條邊即可。


