Python金融大資料分析——第9章 數學工具 筆記
第9章 數學工具
9.1 逼近法
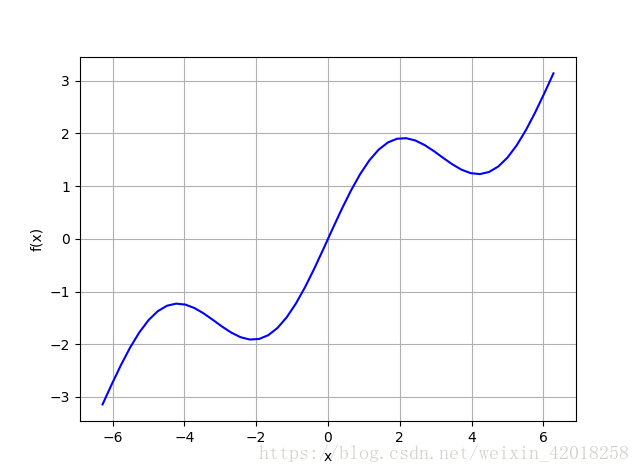
在給定區間內通過迴歸和差值求取該函式的近似值。 首先,我們生成該函式的圖形, 更好地觀察逼近法所實現的結果。我們感興趣的區間是[-2π,2π]。下圖顯示了該函式在通過linspace函式定義的固定區間上的影象。np.linspace(start, stop,num)返回從 star 開始 , stop 結束的 num 個點, 兩個連續點之間的子區間均勻分佈:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return np.sin(x) + 0.5 * x
x = np.linspace(-2 9.1.1 迴歸
迴歸是相當高敬的函式近似值計算工具。 它不僅合求取一維函式的近似值, 在更高維度上也很有效。 得出迴歸結果所需要的數值化方法很容易實現. 執行也很快速。 本質上, 迴歸的任務是在給定一組所謂 “基函式” bd,d∈{1,…,D} 的情況下,根據下面的公式找出最優引數,其中對於i∈{1,…I}觀察點,yi ≡ f(xi)。xi 可以視為自變數觀測值,yi 可以視為因變數觀測值。
最小化迴歸問題公式:
1. 作為基函式的單項式
最簡單的情況是以單項式作為基函式——也就是說 在這種情況下,NumPy有確定最優引數(polyfit)和以一組輸入值求取近似值(polyval ) 的內建函式。
polyfit函式引數
| 引數 | 描述 |
|---|---|
| x | x座標(自變數值) |
| y | y座標(因變數值) |
| deg | 多項式擬合度 |
| full | 如果為真返回額外的診斷資訊 |
| w | 應用到y座標的權重 |
| cov | 如果為真返回協方差矩陣 |
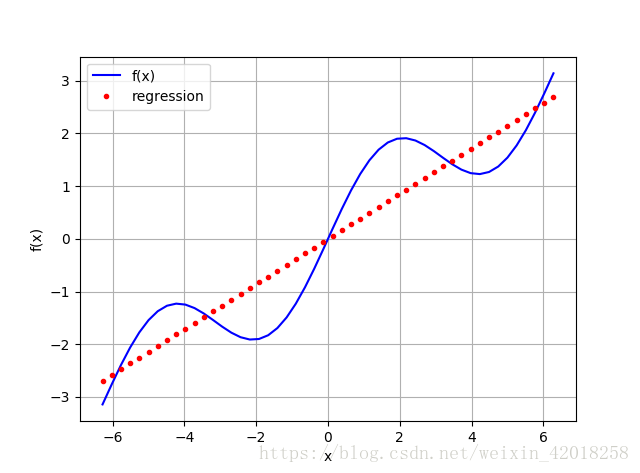
# 典型向量化風格的polyfit和polyval線性迴歸(deg=1)
# 使用 1 次單項式作為基函式
reg = np.polyfit(x, f(x), deg=1)
ry = np.polyval(reg, x)
plt.plot(x, f(x), 'b', label='f(x)')
plt.plot(x, ry, 'r.', label='regression')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')
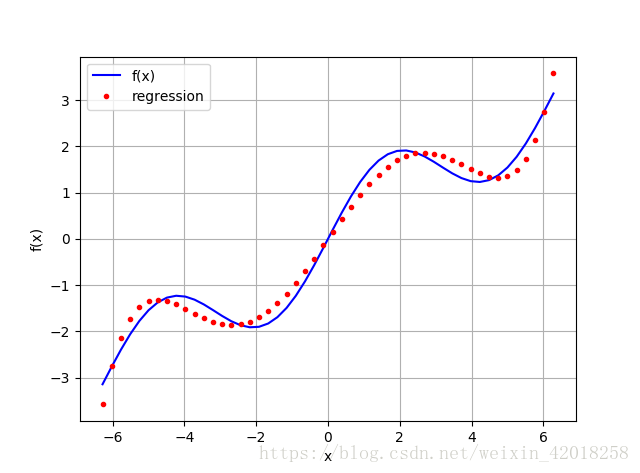
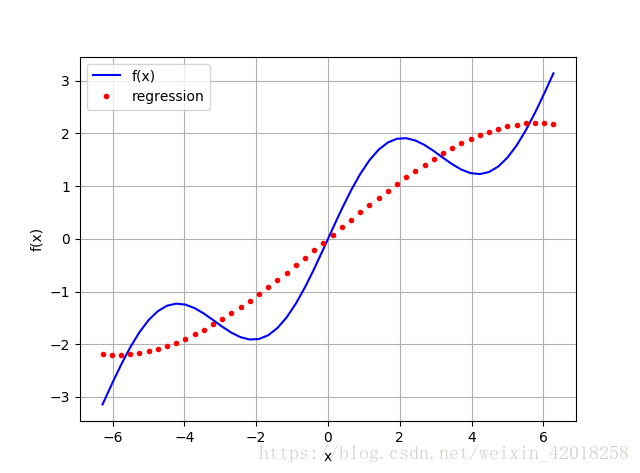
# 使用 5 次單項式作為基函式
reg = np.polyfit(x, f(x), deg=5)
ry = np.polyval(reg, x)
plt.plot(x, f(x), 'b', label='f(x)')
plt.plot(x, ry, 'r.', label='regression')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
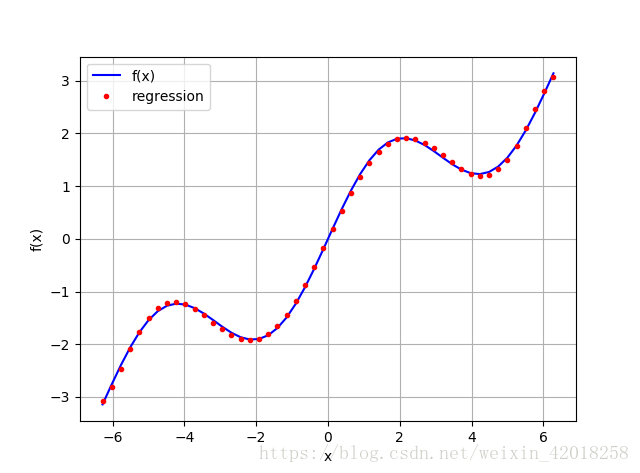
plt.ylabel('f(x)')# 使用 7 次單項式作為基函式
reg = np.polyfit(x, f(x), deg=7)
ry = np.polyval(reg, x)
plt.plot(x, f(x), 'b', label='f(x)')
plt.plot(x, ry, 'r.', label='regression')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')np.allclose(f(x), ry)
# False
np.sum((f(x) - ry) ** 2) / len(x)
# 0.0017769134759517721簡單的檢查表明結果並不完美,但是, 均方差(MSE)不是太大——至少在較窄的 x 值區間內。
2. 單獨的基函式
一般來說, 當選擇更好的基函式組時, 可以得到更好的迴歸結果, 例如利用對函式的認識進行近似值計算。在這種情下,單獨的基函式必須通過一個矩陣方法定義(也就是使用NumPy ndarray物件)。
matrix = np.zeros((3 + 1, len(x)))
matrix[3, :] = x ** 3
matrix[2, :] = x ** 2
matrix[1, :] = x
matrix[0, :] = 1
reg = np.linalg.lstsq(matrix.T, f(x))[0]
reg
# array([ 1.52685368e-14, 5.62777448e-01, -1.11022302e-15,
# -5.43553615e-03])
ry = np.dot(reg, matrix)
plt.plot(x, f(x), 'b', label='f(x)')
plt.plot(x, ry, 'r.', label='regression')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
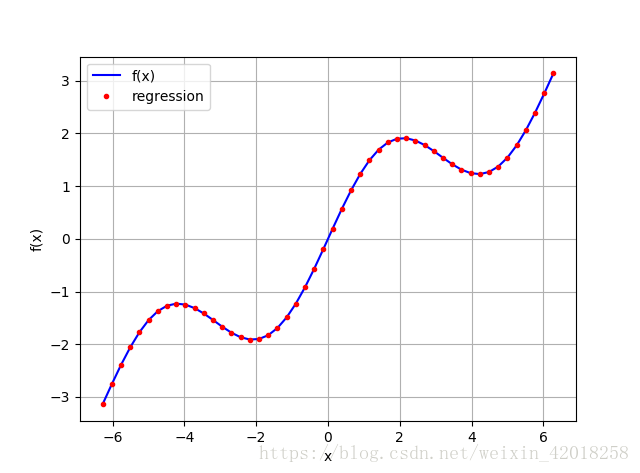
plt.ylabel('f(x)')圖中的結果並不真的如預期那麼好。使用更通用的方法,可以利用對示例函式的認識。我們知道函式中有一個 sin 部分。因此,在基函式中包含一個正弦函式是有意義的。 為了簡單起見. 我們替換最高次的單項式:
matrix[3, :] = np.sin(x)
reg = np.linalg.lstsq(matrix.T, f(x))[0]
ry = np.dot(reg, matrix)
plt.plot(x, f(x), 'b', label='f(x)')
plt.plot(x, ry, 'r.', label='regression')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')np.allclose(f(x),ry)
# True
np.sum((f(x) - ry) ** 2) / len(x)
# 2.1855453008906352e-31
reg
# array([ 9.26243218e-17, 5.00000000e-01, 0.00000000e+00,
# 1.00000000e+00])上面恢復了正確的引數:sin部分為1,線性部分為0.5
原方程為:sin(x) + 0.5 * x
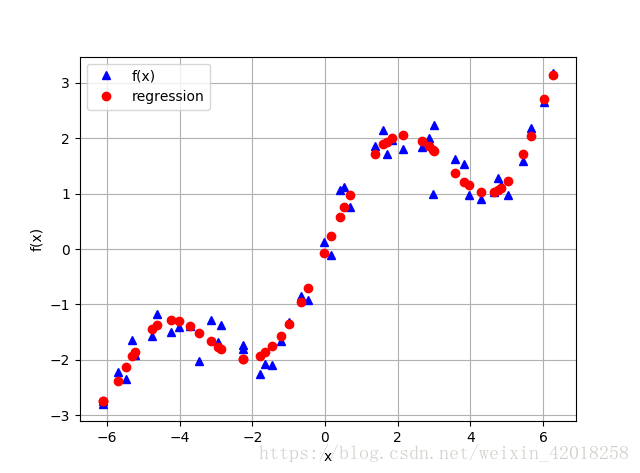
3. 有噪聲的資料
迴歸對於有噪聲的資料同樣能夠很好的處理,這種資料來自於模擬或者(不完善的)測量。 為了闡述這個要點,我們生成同樣具有噪聲的自變數觀測值和因變數觀測值:
xn = np.linspace(-2 * np.pi, 2 * np.pi, 50)
xn = xn + 0.15 * np.random.standard_normal(len(xn))
yn = f(xn) + 0.25 * np.random.standard_normal(len(xn))
reg = np.polyfit(xn, yn, 7)
ry = np.polyval(reg, xn)
plt.plot(xn, yn, 'b^', label='f(x)')
plt.plot(xn, ry, 'ro', label='regression')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
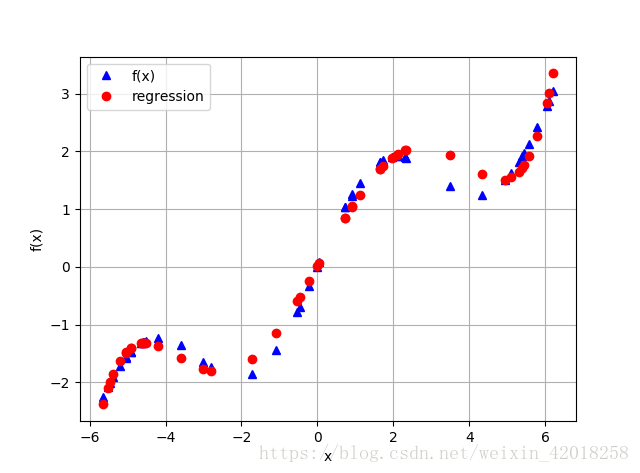
plt.ylabel('f(x)')4. 未排序資料
迴歸的另一個重要特點是這種方法可以無縫地處理未排序資料。前面的例子都依賴於經過排序的x資料, 情況並不總是這樣的, 為了說明這一點, 我們隨機產生自變數資料點:
xu = np.random.rand(50) * 4 * np.pi - 2 * np.pi
yu = f(xu)
# 在這種情況下,僅靠從視覺上檢查原始資料很難識別出任何結構:
print(xu[:10].round(2))
print(yu[:10].round(2))
# [ 4.94 6.05 2.34 5.8 5.39 2.13 -0.54 6.11 0.9 -5.52]
# [ 1.5 2.79 1.89 2.43 1.91 1.91 -0.78 2.88 1.23 -2.07]
# 和有噪聲資料一樣,迴歸方法不關心觀測點的順序。
reg = np.polyfit(xu, yu, 5)
ry = np.polyval(reg, xu)
plt.plot(xu, yu, 'b^', label='f(x)')
plt.plot(xu, ry, 'ro', label='regression')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')5. 多維
最小二乘迴歸方法的另一個便利特性是不需要太多的修改就可以用於多維的情況,以下面介紹的fm函式為例:
def fm(x, y):
return np.sin(x) + 0.25 * x + np.sqrt(y) + 0.05 * y ** 2
x = np.linspace(0, 10, 20)
y = np.linspace(0, 10, 20)
X, Y = np.meshgrid(x, y)
# generates 2-d grids out of the 1-d arrays
Z = fm(X, Y)
x = X.flatten()
y = Y.flatten()
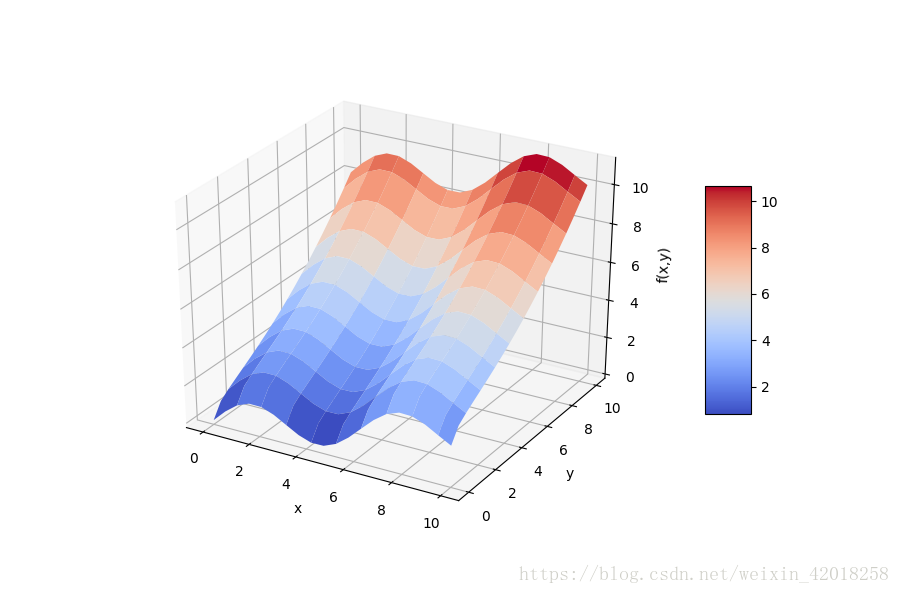
# 根據以 x,y,z 表示的自變數和因變數資料點網格,顯示fm函式的形狀
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
fig = plt.figure(figsize=(9, 6))
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=mpl.cm.coolwarm, linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
fig.colorbar(surf, shrink=0.5, aspect=5)
為了獲得好的迴歸結果,我們編輯一組基函式,包括一個sin 和 一個 sqrt 函式,利用了我們對函式的認識:
matrix = np.zeros((len(x), 6 + 1))
matrix[:, 6] = np.sqrt(y)
matrix[:, 5] = np.sin(x)
matrix[:, 4] = y ** 2
matrix[:, 3] = x ** 2
matrix[:, 2] = y
matrix[:, 1] = x
matrix[:, 0] = 1
# statsmodels庫提供了相當通用和有益的函式OLS,可以用於一維和多維最小二乘迴歸
import statsmodels.api as sm
model = sm.OLS(fm(x, y), matrix).fit()
# OLS 函式的好處之一是提供關於迴歸及其質量的大量附加資訊。 呼叫 model.summary可以訪問結果的一個摘要。單獨統計數字(如 確定係數)通常可以直接的問
model.rsquared
# 1.0
a = model.params
a
# array([ -4.37150316e-15, 2.50000000e-01, 1.88737914e-15,
# -2.93168267e-16, 5.00000000e-02, 1.00000000e+00,
# 1.00000000e+00])reg_func返回給定最優迴歸引數和自變數資料點的迴歸函式值:
def reg_func(a, x, y):
f6 = a[6] * np.sqrt(y)
f5 = a[5] * np.sin(x)
f4 = a[4] * y ** 2
f3 = a[3] * x ** 2
f2 = a[2] * y
f1 = a[1] * x
f0 = a[0] * 1
return (f6 + f5 + f4 + f3 + f2 + f1 + f0)將這些值與示例函式原始構成比較
RZ = reg_func(a, X, Y)
fig = plt.figure(figsize=(9, 6))
ax = fig.gca(projection='3d')
surf1 = ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=mpl.cm.coolwarm, linewidth=0.5, antialiased=True)
surf2 = ax.plot_surface(X, Y, RZ, rstride=2, cstride=2, label='regression')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.legend()
fig.colorbar(surf1, shrink=0.5, aspect=5)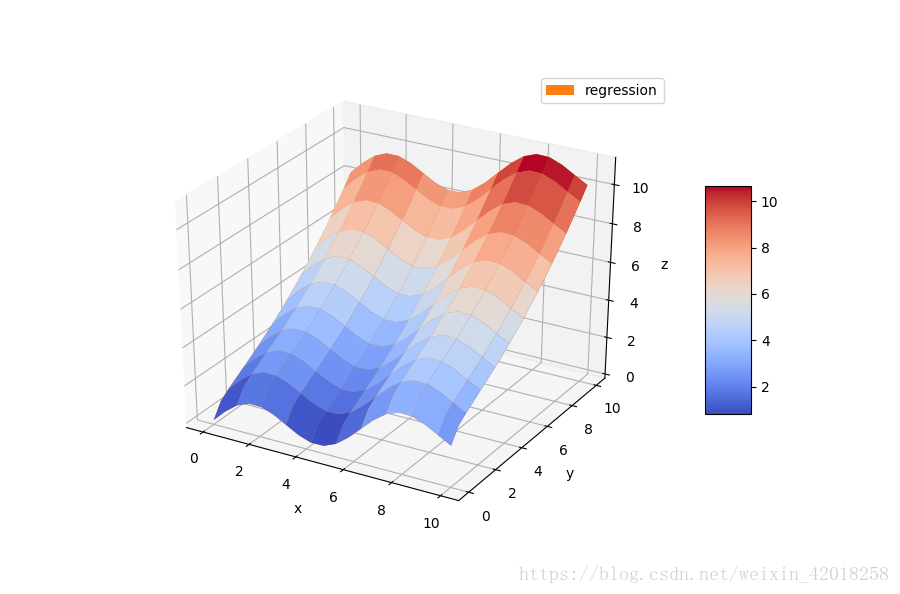
迴歸
最小二乘迴歸方法有多種應用領域, 包括簡單的函式逼近和基於有噪聲或者未排序資料的函式逼近。 這些方法可以應用於一維問題, 也可以應用於多維問題。 由於這種方法的基礎數學理論使然, 在一維問題和多維問題上的應用總是 “幾乎相同”
9.1.2 插值
與迴歸相比, 插值〈例如, 三次樣條插值)在數學上更為複雜。 它還被限制在低維度問題上。給定一組有序的觀測點(按照x維排序), 基本的思路是在兩個相鄰資料點之間進行迴歸。不僅產生的分段插值函式完全匹配資料點, 而且函式在資料點上連續可微分。 連續可微分性需要至少三階插值一一也就是三次樣條插值。 然而, 這種方法一般也適用於四次甚至線性樣條插值。
在給定以x排序的資料點集時, 應用這種方法和polyft、polyval 一樣簡單, 此時對應的函式是splrep和splev。
splrep函式引數
| 引數 | 描述 |
|---|---|
| x | (有序)x座標(自變數值) |
| y | (按x排序)y座標(因變數值) |
| w | 應用到y座標的權重 |
| xb,xe | 擬合區間,如果設定為None則區間為[x[0],[-1]] |
| k | 樣條擬合順序(1<=k<=5) |
| s | 平滑因子 |
| full_output | 如果為真,返回附加輸出 |
| quiet | 如果為真,抑制訊息 |
splev函式引數
| 引數 | 描述 |
|---|---|
| x | (有序)x座標(自變數值) |
| tck | splrep返回的長度為3的序列(節點,係數,階數) |
| der | 導數的階(0為元函式,1為一階導數) |
| ext | 如果x不在節點序列中時的行為(0外推,1返回0,2引發ValueError異常) |
import numpy as np
import scipy.interpolate as spi
import matplotlib.pyplot as plt
x = np.linspace(-2 * np.pi, 2 * np.pi, 25)
def f(x):
return np.sin(x) + 0.5 * x
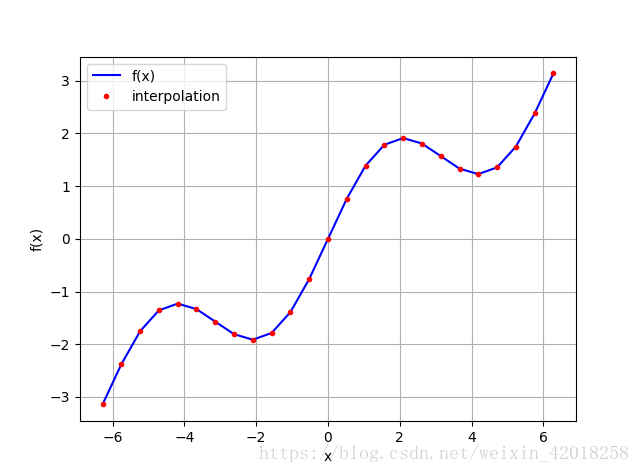
ipo = spi.splrep(x, f(x), k=1)
iy = spi.splev(x, ipo)
plt.plot(x, f(x), 'b', label='f(x)')
plt.plot(x, iy, 'r.', label='interpolation')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')np.allclose(f(x),iy)
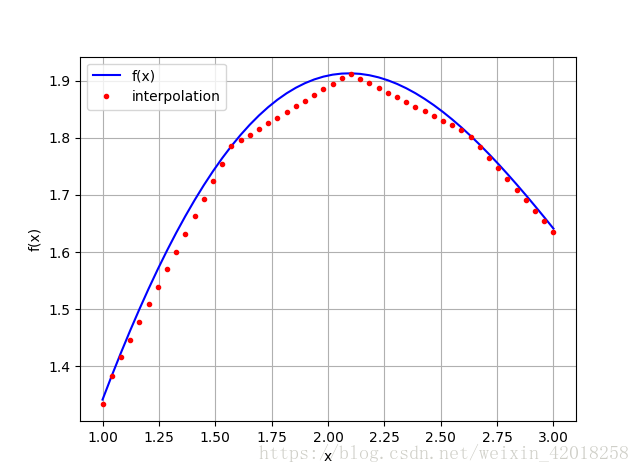
# True樣條插值在金融學中往往用於估算未包含在原始觀測點中的自變數資料點的因變數值。 為次,我們選擇一個更小的區間 , 仔細觀察一次樣條插入的值:
xd = np.linspace(1.0, 3.0, 50)
iyd = spi.splev(xd, ipo)
plt.plot(xd, f(xd), 'b', label='f(x)')
plt.plot(xd, iyd, 'r.', label='interpolation')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')插值函式確實線性地在兩個觀測點之間插值。 對於某些應用, 這可能不夠精確。此外, 很明顯函式在原始資料點上不是連續可微分的一一這是另一個不足
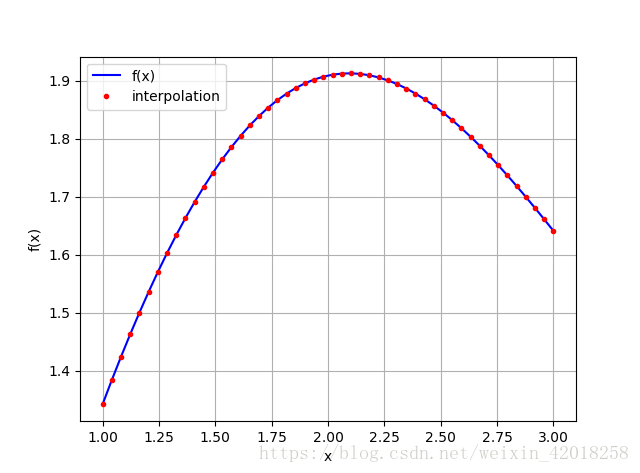
這次使用三次樣條插值:
ipo = spi.splrep(x, f(x), k=3)
iyd = spi.splev(xd, ipo)
plt.plot(xd, f(xd), 'b', label='f(x)')
plt.plot(xd, iyd, 'r.', label='interpolation')
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')np.allclose(f(xd), iyd)
# False
np.sum((f(xd)-iyd)**2)/len(xd)
# 1.1349319851436252e-08從數值上看, 這種插值並不完美,但是MSE確實很小。
插值
在可以應用樣條插值的情況下, 可以預期比最小二來回歸方法更好的近似結果。 但是要記住, 你必須有排序(且“無噪聲”)的資料, 該方法僅限於低維度問題。 樣條插值的計算要求也更高, 在某些用例中可能導致花費的時間比迴歸方法長得多。
9.2 凸優化
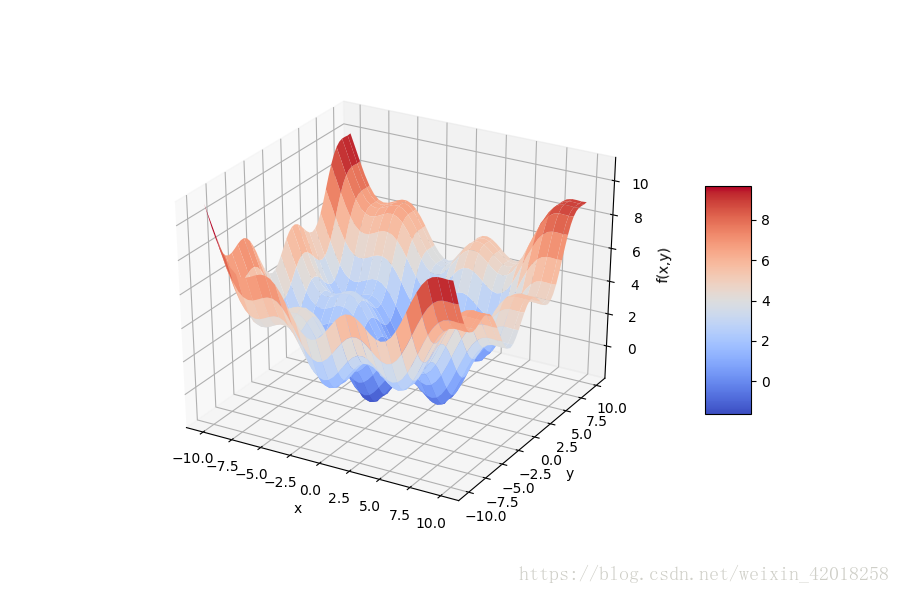
在金融學和經濟學中, 凸優化起著重要的作用。 這方面的例子包括根據市場資料校準期權定價模型, 或者效用函式的優化。我們以下面定義的函式 fm 為例進行這種優化:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
def fm(x, y):
return (np.sin(x) + 0.05 * x ** 2 + np.sin(y) + 0.05 * y ** 2)
x = np.linspace(-10, 10, 50)
y = np.linspace(-10, 10, 50)
X, Y = np.meshgrid(x, y)
Z = fm(X, Y)
fig = plt.figure(figsize=(9, 6))
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=mpl.cm.coolwarm, linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
fig.colorbar(surf, shrink=0.5, aspect=5)9.2.1 全域性優化
為了更仔細地觀察初始化最小化過程時後臺發生的情況, 我們改善原函式, 通過一個選項輸出當前引數值和函式值:
output = True
def fo(x):
z = np.sin(x[0]) + 0.05 * x[0] ** 2 + np.sin(x[1]) + 0.05 * x[1] ** 2
if output == True:
print('%8.4f %8.4f %8.4f' % (x[0], x[1], z))
return zbrute以引數範圍作為輸入。 例如, 提供x值範圍(- 10, 10.1, 5 )會得到, -10、 -5 、 0 、 5 、 10這5個 “測試值 ” :
import scipy.optimize as spo
output = True
spo.brute(fo, ((-10, 10.1, 5), (-10, 10.1, 5)), finish=None)
# -10.0000 -10.0000 11.0880
# -10.0000 -10.0000 11.0880
# -10.0000 -5.0000 7.7529
# -10.0000 0.0000 5.5440
# -10.0000 5.0000 5.8351
# -10.0000 10.0000 10.0000
# -5.0000 -10.0000 7.7529
# -5.0000 -5.0000 4.4178
# -5.0000 0.0000 2.2089
# -5.0000 5.0000 2.5000
# -5.0000 10.0000 6.6649
# 0.0000 -10.0000 5.5440
# 0.0000 -5.0000 2.2089
# 0.0000 0.0000 0.0000
# 0.0000 5.0000 0.2911
# 0.0000 10.0000 4.4560
# 5.0000 -10.0000 5.8351
# 5.0000 -5.0000 2.5000
# 5.0000 0.0000 0.2911
# 5.0000 5.0000 0.5822
# 5.0000 10.0000 4.7471
# 10.0000 -10.0000 10.0000
# 10.0000 -5.0000 6.6649
# 10.0000 0.0000 4.4560
# 10.0000 5.0000 4.7471
# 10.0000 10.0000 8.9120
# array([ 0., 0.])在給定的函式初始引數化條件下, 最優化引數值是x=y=0。 回顧前面的輸出可以看出,結果函式值也為0。第一次引數化相當粗糙,我們對兩個輸人蔘數均使用5的步距。這當然有很大的微調空間, 得到更好的結果:
output = False
opt1 = spo.brute(fo, ((-10, 10.1, 0.1), (-10, 10.1, 0.1)), finish=None)
opt1
# array([-1.4, -1.4])
fm(opt1[0], opt1[1])
# -1.7748994599769203
最優化引數值現在是 x=y=1.4, 全域性最小化的最小函式值大約為-1.7749
9.2.2 區域性優化
對於區域性凸優化,我們打算利用全域性優化的結果。fmin函式的輸人是需要最小化的函式和起始引數值。此外,可以定義輸入引數寬容度和函式值寬容度, 以及最大迭代及函式呼叫次數:
output = True
opt2 = spo.fmin(fo, opt1, xtol=0.001, ftol=0.001, maxiter=15, maxfun=20)
opt2
# -1.4000 -1.4000 -1.7749
# -1.4700 -1.4000 -1.7743
# -1.4000 -1.4700 -1.7743
# -1.3300 -1.4700 -1.7696
# -1.4350 -1.4175 -1.7756
# -1.4350 -1.3475 -1.7722
# -1.4088 -1.4394 -1.7755
# -1.4438 -1.4569 -1.7751
# -1.4328 -1.4427 -1.7756
# -1.4591 -1.4208 -1.7752
# -1.4213 -1.4347 -1.7757
# -1.4235 -1.4096 -1.7755
# -1.4305 -1.4344 -1.7757
# -1.4168 -1.4516 -1.7753
# -1.4305 -1.4260 -1.7757
# -1.4396 -1.4257 -1.7756
# -1.4259 -1.4325 -1.7757
# -1.4259 -1.4241 -1.7757
# -1.4304 -1.4177 -1.7757
# -1.4270 -1.4288 -1.7757
# Warning: Maximum number of function evaluations has been exceeded.
# array([-1.42702972, -1.42876755])
fm(opt2[0], opt2[1])
# -1.7757246992239009我們可以觀察到解決方案的徽調和更低的函式值。
在許多凸優化問題中, 建議在區域性優化之前進行全域性優化。 主要原因是區域性凸優化演算法很容易陷人某個區域性最小值(所謂的 “盆地跳躍 ” ( basin hopping)), 而忽略“更好”的區域性最小值和全域性最小值。下面可以看到’ 將初始引數化設定為x=y=2得出高於0的“最小”值:
output = False
opt3 = spo.fmin(fo, (2.0, 2.0), maxiter=250)
# Optimization terminated successfully.
# Current function value: 0.015826
# Iterations: 46
# Function evaluations: 86
# Out[11]: array([ 4.2710728 , 4.27106945])
fm(opt3[0], opt3[1])
# 0.0158257532746804999.2.3 有約束優化
目前為止, 我們只考慮了無約束優化問題。但是許多型別的經濟學或者金融學優化問題都有 一個或者多個約束條件。 這些約束可能採取等式或者不等式等正規形式。
舉個簡單的例子, 考慮可能投資於兩種高風險證券(希望效用最大化)的投資者的效用最大化問題。 兩種證券今天的價格為。 一年之後, 狀態 u 下它們的收益分別為15美元和5美元,而在狀態 d 下收益分別為5美元和12美元。 兩種狀態的出現可能性相同。兩種證券的向盤收益分別記為和。
投資者的投資頂算為