快速理解平衡二叉樹、B-tree、B+tree、B*tree
1、平衡二叉樹
(1)由來:平衡二叉樹是基於二分法的策略提高資料的查詢速度的二叉樹的資料結構;
(2)特點:
平衡二叉樹是採用二分法思維把資料按規則組裝成一個樹形結構的資料,用這個樹形結構的資料減少無關資料的檢索,大大的提升了資料檢索的速度;平衡二叉樹的資料結構組裝過程有以下規則:
非葉子節點只能允許最多兩個子節點存在,每一個非葉子節點資料分佈規則為左邊的子節點小當前節點的值,右邊的子節點大於當前節點的值(這裡值是基於自己的演算法規則而定的,比如hash值);
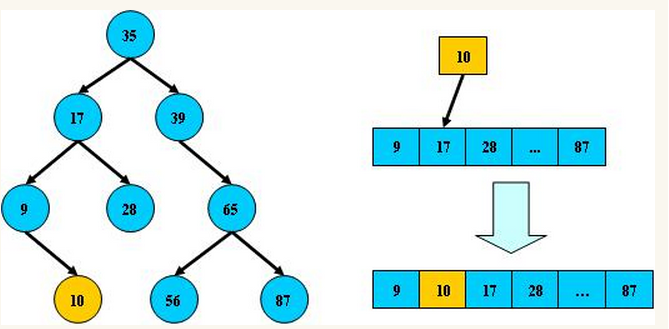
平衡樹的層級結構:因為平衡二叉樹查詢效能和樹的層級(h高度)成正比、為了保證樹的結構左右兩端資料大致平衡降低二叉樹的查詢難度一般會採用一種演算法機制實現節點資料結構的平衡,實現了這種演算法的有比如AVL、
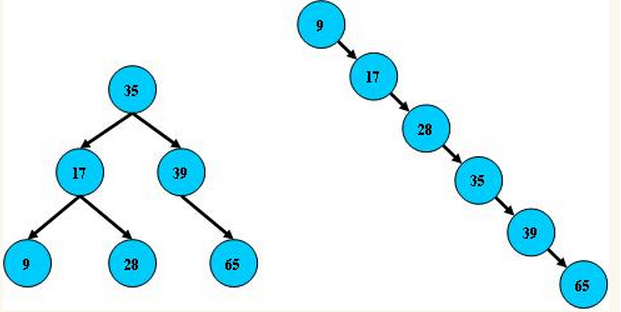
總結平衡二叉樹特點:
(1)非葉子節點最多擁有兩個子節點;
(2)非葉子節值大於左邊子節點、小於右邊子節點;
(3)樹的左右兩邊的層級數相差不會大於1;
(4)沒有值相等重複的節點;
2、B樹(B-tree)
注意:之前有看到有很多文章把B樹和B-tree理解成了兩種不同類別的樹,其實這兩個是同一種樹;
1、概念:B樹和平衡二叉樹稍有不同的是B樹屬於多叉樹又名平衡多路查詢樹(查詢路徑不只兩個),資料庫索引技術裡大量使用者B樹和B+樹的資料結構,讓我們來看看他有什麼特點;
2、規則:
(1)樹種的每個節點最多擁有m個子節點且m>=2,空樹除外(注:m階代表一個樹節點最多有多少個查詢路徑,m階=m路,當m=2則是2叉樹,m=3則是3叉);
(2)除根節點外每個節點的關鍵字數量大於等於ceil(m/2)-1個小於等於m-1個;(注:ceil()是個朝正無窮方向取整的函式 如ceil(1.1)結果為2)
(3)所有葉子節點均在同一層、葉子節點除了包含了關鍵字和關鍵字記錄的指標外也有指向其子節點的指標只不過其指標地址都為null對應下圖最後一層節點的空格子
(4)如果一個非葉節點有N個子節點,則該節點的關鍵字數等於N-1;
(5)所有節點關鍵字是按遞增次序排列,並遵循左小右大原則;
最後我們用一個圖和一個實際的例子來理解B樹(這裡為了理解方便我就直接用實際字母的大小來排列C>B>A)
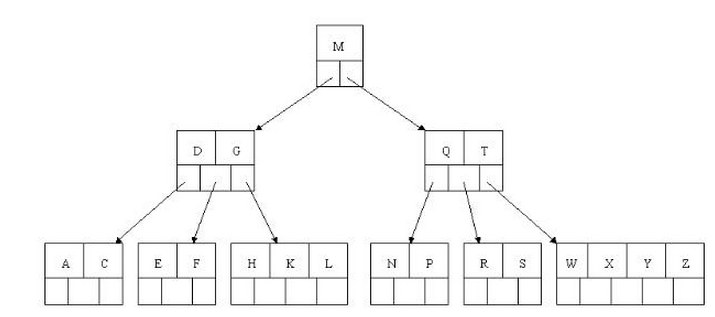
3、B樹的查詢流程: 如上圖我要從上圖中找到E字母,查詢流程如下
(1)獲取根節點的關鍵字進行比較,當前根節點關鍵字為M,E要小於M(26個字母順序),所以往找到指向左邊的子節點(二分法規則,左小右大,左邊放小於當前節點值的子節點、右邊放大於當前節點值的子節點);
(2)拿到關鍵字D和G,D<E<G 所以直接找到D和G中間的節點;
(3)拿到E和F,因為E=E 所以直接返回關鍵字和指標資訊(如果樹結構裡面沒有包含所要查詢的節點則返回null);
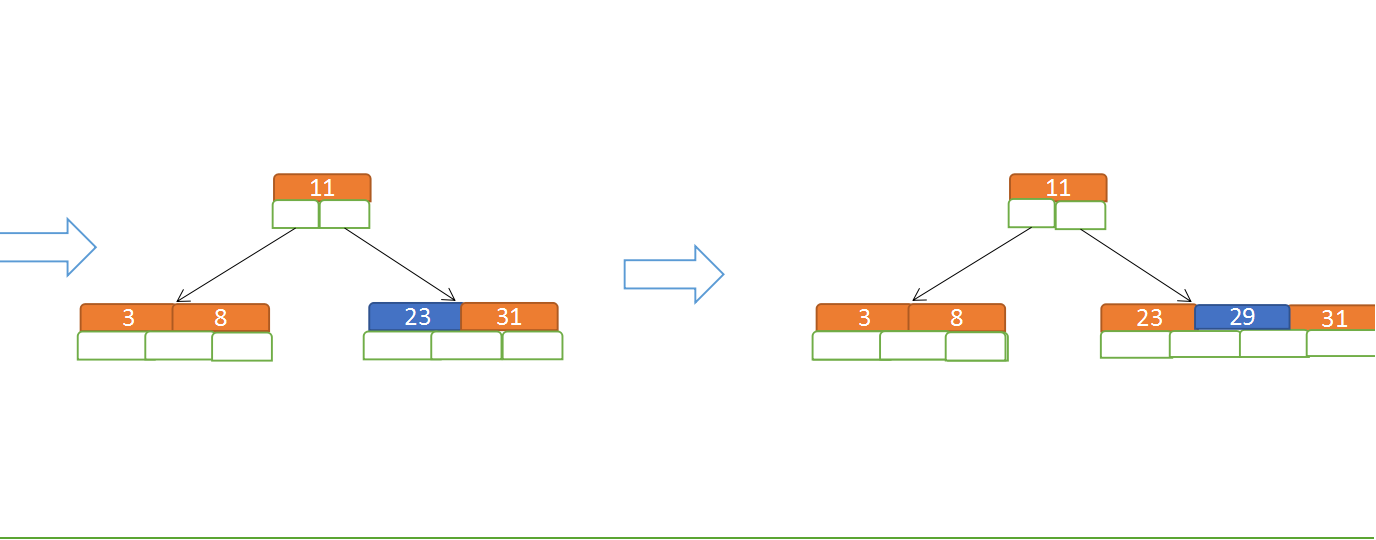
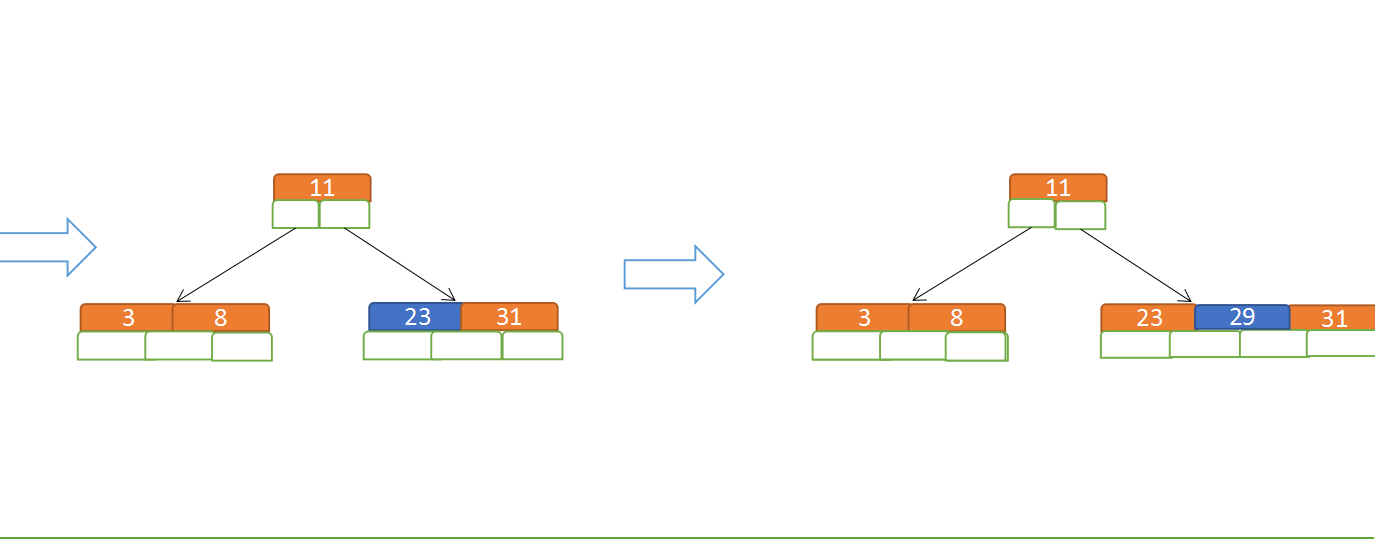
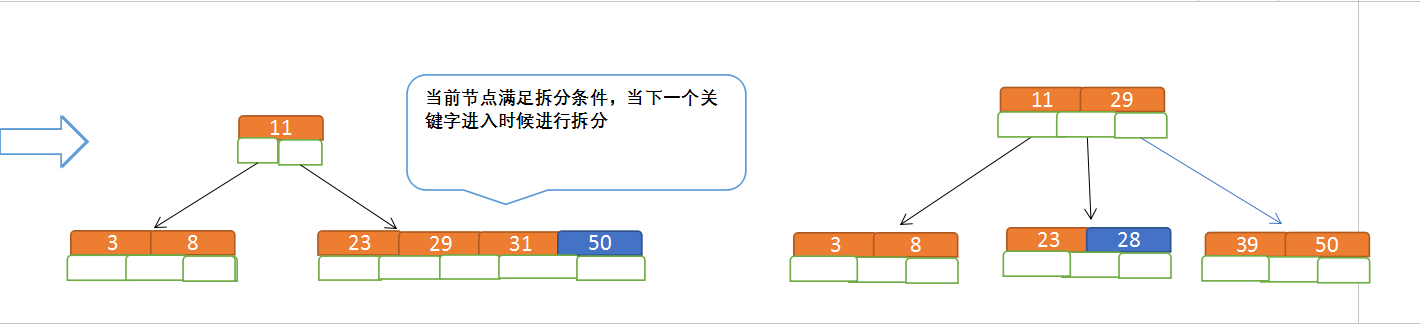
4、B樹的插入節點流程
定義一個5階樹(平衡5路查詢樹;),現在我們要把3、8、31、11、23、29、50、28 這些數字構建出一個5階樹出來;
遵循規則:
(1)當前是要組成一個5路查詢樹,那麼此時m=5,關鍵字數必須大於等於cei(5/2)-1小於等於5-1(關鍵字數小於cei(5/2)-1 就要進行節點合併,大於5-1就要進行節點拆分);
(2)滿足左大右小的排序規則;
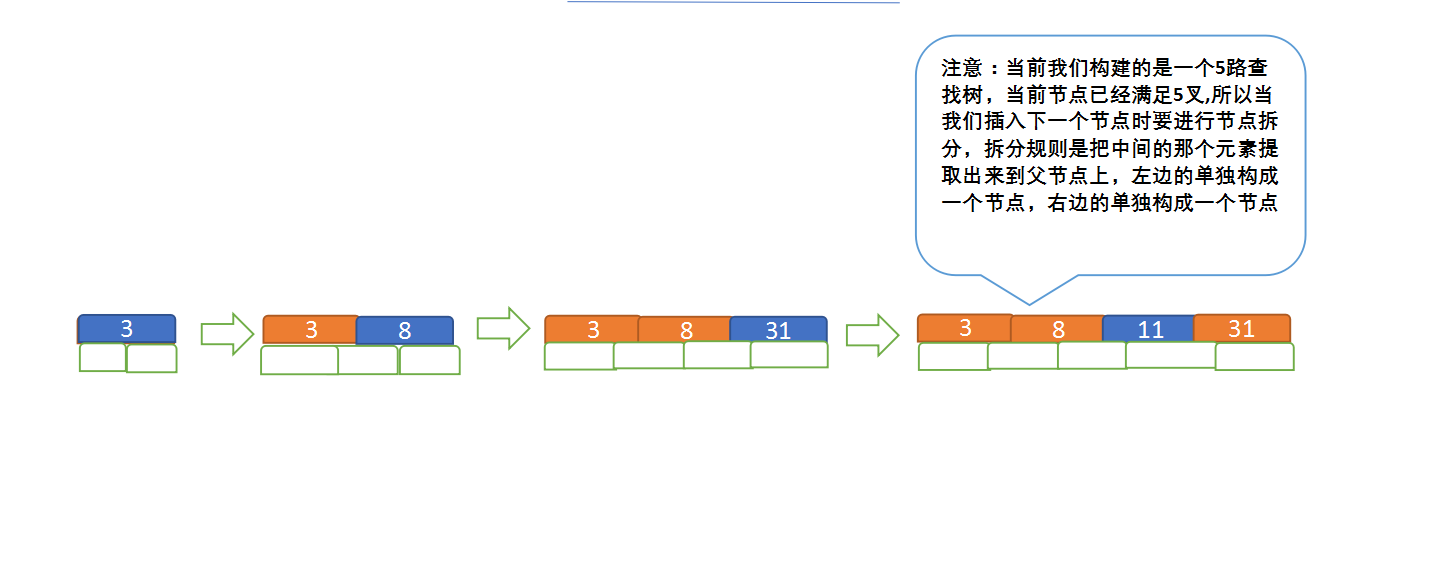
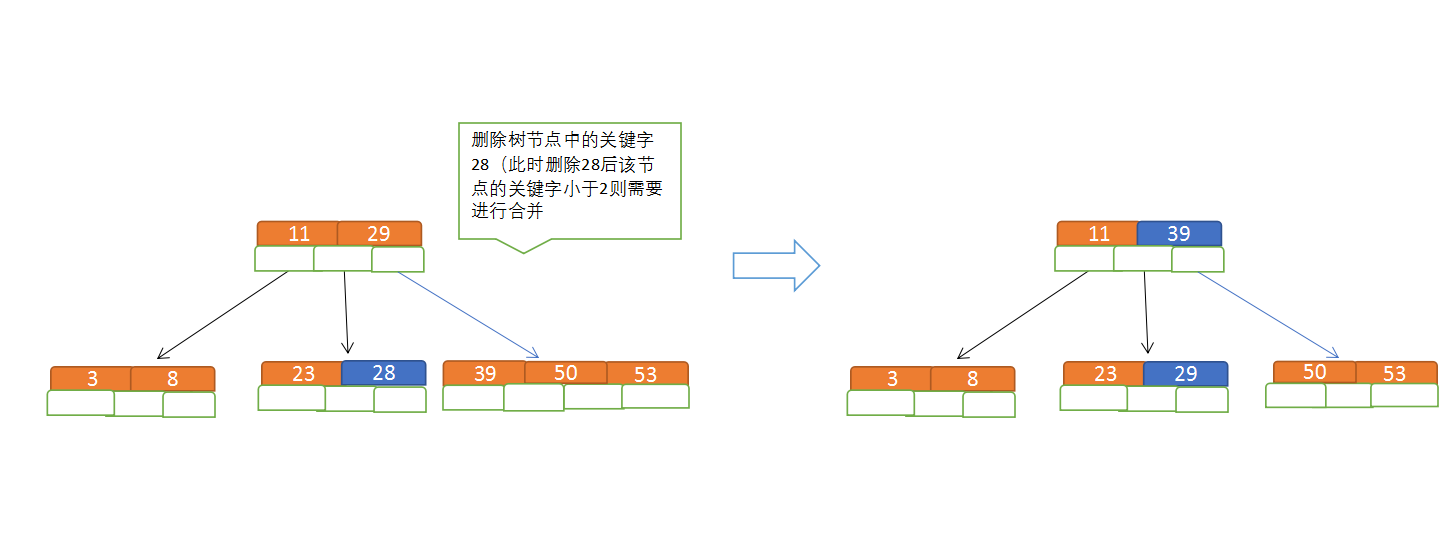
5、B樹節點的刪除
規則:
(1)當前是要組成一個5路查詢樹,那麼此時m=5,關鍵字數必須大於等於cei(5/2)-1小於等於5-1;
(2)滿足左大右小的排序規則;
(3)關鍵字數小於二時先從子節點取,子節點沒有符合條件時就向向父節點取,取中間值往父節點放;
3、特點:
B樹相對於平衡二叉樹的不同是,每個節點包含的關鍵字增多了,特別是在B樹應用到資料庫中的時候,資料庫充分利用了磁碟塊的原理(磁碟資料儲存是採用塊的形式儲存的,每個塊的大小一般為4K,每次IO進行資料讀取時,同一個磁碟塊的資料可以一次性讀取出來)把節點大小限制和充分使用在磁碟快大小範圍;把樹的節點關鍵字增多後樹的層級比原來的二叉樹少了,減少資料查詢的次數和複雜度;
3、B+樹
B+樹是B樹的一個升級版,相對於B樹來說B+樹更充分的利用了節點的空間,讓查詢速度更加穩定,其速度完全接近於二分法查詢。為什麼說B+樹查詢的效率要比B樹更高、更穩定;我們先看看兩者的區別
(1)B+跟B樹不同B+樹的非葉子節點不儲存關鍵字記錄的指標,這樣使得B+樹每個節點所能儲存的關鍵字大大增加;
(2)B+樹葉子節點儲存了父節點的所有關鍵字和關鍵字記錄的指標,每個葉子節點的關鍵字從小到大連結;
(3)B+樹的根節點關鍵字數量和其子節點個數相等;
(4)B+的非葉子節點只進行資料索引,不會存實際的關鍵字記錄的指標,所有資料地址必須要到葉子節點才能獲取到,所以每次資料查詢的次數都一樣;
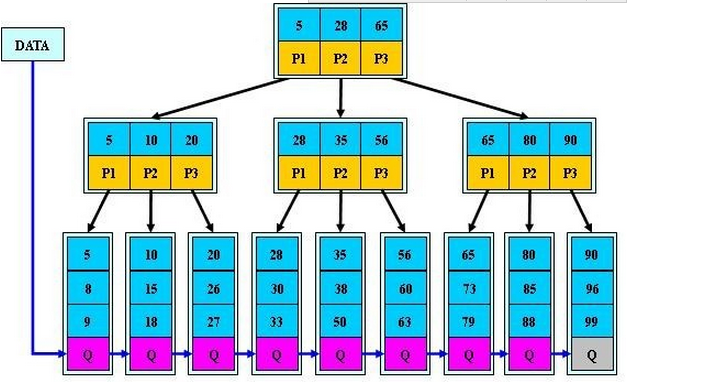
特點:
在B樹的基礎上每個節點儲存的關鍵字數更多,樹的層級更少所以查詢資料更快,所有指關鍵字指標都存在葉子節點,所以每次查詢的次數都相同所以查詢速度更穩定;
4、B*樹
B*樹是B+樹的變種,相對於B+樹他們的不同之處如下:
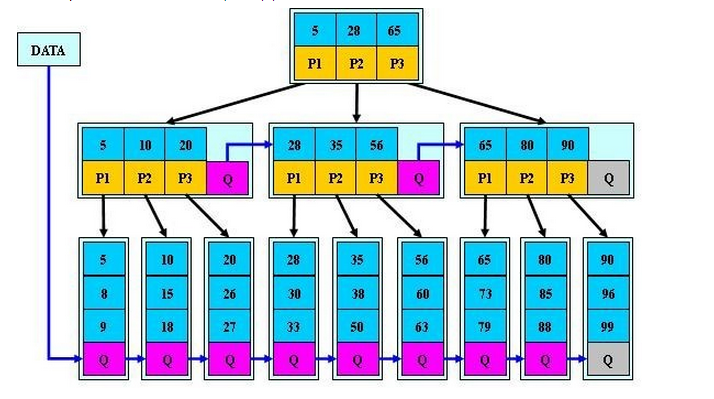
(1)首先是關鍵字個數限制問題,B+樹初始化的關鍵字初始化個數是cei(m/2),b*樹的初始化個數為(cei(2/3*m))
(2)B+樹節點滿時就會分裂,而B*樹節點滿時會檢查兄弟節點是否滿(因為每個節點都有指向兄弟的指標),如果兄弟節點未滿則向兄弟節點轉移關鍵字,如果兄弟節點已滿,則從當前節點和兄弟節點各拿出1/3的資料建立一個新的節點出來;
特點:
在B+樹的基礎上因其初始化的容量變大,使得節點空間使用率更高,而又存有兄弟節點的指標,可以向兄弟節點轉移關鍵字的特性使得B*樹額分解次數變得更少;
總結:從平衡二叉樹、B樹、B+樹、B*樹總體來看它們的貫徹的思想是相同的,都是採用二分法和資料平衡策略來提升查詢資料的速度;
不同點是他們一個一個在演變的過程中通過IO從磁碟讀取資料的原理進行一步步的演變,每一次演變都是為了讓節點的空間更合理的運用起來,從而使樹的層級減少達到快速查詢資料的目的;
如果還沒理解的話推薦以下資料描敘的很詳細:
推薦資料:
附二(B、B+、B*樹):http://blog.csdn.net/v_JULY_v/article/details/6530142/
附三(B、B+、B*樹):http://blog.csdn.net/endlu/article/details/51720299
