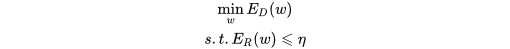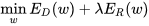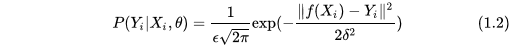（作者：陳玓玏）

1、 為什麼要正則化?

知乎上有個兄弟說得對（https://www.zhihu.com/question/20924039 這個問題下Stark Einstein的回答），不應該說是正則化，應該說是規則化，也就是說，我們原來是在完全沒有任何先驗知識的情況下進行的訓練，那訓練出來的結果有可能會“過”，你不知道哪個特徵會有用，於是你找了很多特徵，儘可能精確地去擬合你的訓練資料，結果用上了一些其實不重要的特徵，這些特徵在訓練集中表現不錯，但是在測試集中卻不重要，也就是說這些特徵本身就不具備普適性，但你還學習到它了，在這種不具備普遍性的情況下學習到它，自然會影響你測試集的效果，自然就做不出泛化能力強的模型，就產生了過擬合。當然了，並不是只要引數一多就會過擬合，還要看你的樣本量。

規則化的另外一個意義是減少不必要的特徵，只剩下那些普遍成立的特徵，既然每個特徵都對應一個引數，那麼我們減少特徵或者降低特徵權重，就是讓引數等於0或接近0。最原始的想法就是用L0範數，因為它表示向量中非零元素的個數，只要把這個控制在一定範圍內，模型複雜度就控制住了。但L0不好求解，因為是NP完全問題，因此求意義接近的L1範數，表示所有引數的絕對值之和。但是L1範數會把一些特徵丟棄，但是大家只想讓它們在最小化結構風險的過程中儘可能小，所以就有了L2範數來進行規則化。

具體的問題我們接下來慢慢討論。

2、 為什麼說正則相當於加入先驗？

那如果我們有了先驗知識呢？規則化就是幫助我們加入先驗知識到學習過程中的。先說個結論：L1正則就是加入拉普拉斯先驗，L2正則就是加入高斯先驗，這個先驗是針對引數來說的。

下面的內容是從知乎上（https://www.zhihu.com/question/23536142 這個回答下Charles Xiao和Thaurun的回答）學到的，算是自己做的筆記，這些博主的部落格也有一些很棒的其他文章，可以學習一下~

規則化=加入先驗資訊這個是從貝葉斯的角度來看的，如果我們考慮一個線性模型，那麼其模型公式為： 這裡的$\epsilon$是白噪聲，用來模擬資料集中的觀測值$\hat Y$與真實值之間的誤差。因此，我們能夠從樣本$X$中預測出真實值$Y$的概率是由白噪聲的概率分佈決定的。既然是白噪聲，那就是符合標準正態分佈的，即它的分佈為$\epsilon$~$N(0,\delta^2)$

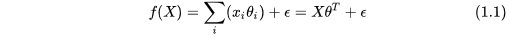
假設樣本之間是獨立的，那麼我們最後得到的整體預測正確的概率為： 根據極大似然估計，我們最後能夠儘可能多地預測正確資料，其概率值和引數$\theta$有關，那麼我們的目標就是找到使式(1.3)概率最大的$\theta$值，對其取log也成立： 第二個等式就是對第一個取log之後的結果，這個結果中的第二項是常數，在優化過程中是可以忽略不計的，第一項的係數也可以忽略不計，並且加負號後轉換成求最小值，優化目標依然成立，但這個形式就已經是最小二乘的形式了，也是我們平時所見到的RMSE損失函式。

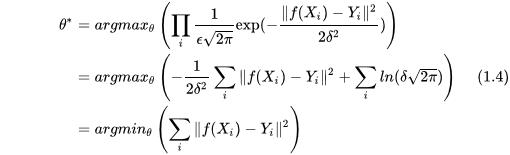
到了這一步我們可以看出來，正則就是在最後一個等式的結果上加了一項，對L1規則化往回推導，那就是在似然函式上乘上以下這一項： $\prod \exp(\lambda |\theta_i|)$ L2規則化往回推導，就是在似然函式乘上這一項： $\prod \exp(\lambda ||\theta_i||^2)$ 這兩項的形式正好一個接近拉普拉斯分佈，一個接近高斯分佈。下面還是順著來看吧。在不考慮$\theta$的分佈時，我們認為它的分佈是個常數，既然現在知道了，那麼極大似然估計的最大化後驗概率中必然要乘上這一項： 拉普拉斯分佈的概率密度函式： 我們可以認為$\lambda=\frac{1}{b}$，$\mu = 0$，這就很接近我們剛才反推的結果了，最後把這個概率值乘上式（1.3）後再簡化，結果如下： 同理，高斯分佈的概率密度函式中，取$\mu =0$,$\lambda=\frac{1}{2\delta^2}$。

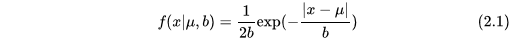
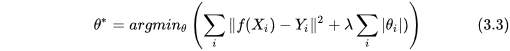
3、 為什麼L1稀疏L2平滑？

從上面兩個概率公式中能看出些苗頭，首先，拉普拉斯分佈圖是這樣的： 高斯分佈的概率分佈圖是這樣的： 我們之前已經討論過了，我們加入的正則是假設引數分佈的均值為0，並且把$\lambda$做了等價，$\lambda$越大，表示拉普拉斯分佈的$b$和高斯分佈的$\delta^2$越小，也就是方差越小，分佈越集中在0附近，因此懲罰因子$\lambda$越大，兩種規則化的結果必然是越來越多的引數接近0，那為什麼我們又會說，L1稀疏，L2平滑呢？

這個從導數上能窺得一二。先寫出L1正則的結構風險導數，L1表示加了L1正則後的結構化風險，L表示規則化以前的結構化風險： $\frac{\partial L1}{\partial \theta}= \frac{\partial L}{\partial \theta}+ \lambda sign(\theta)$ $\frac{\partial L1}{\partial \theta}= \begin{cases} \frac{\partial L}{\partial \theta} + {\lambda}, & \text {if $\theta>0$}\\ \frac{\partial L}{\partial \theta} - {\lambda}, & \text {if $\theta<0$} \end{cases}$ 什麼時候$\theta=0$會是我們要找的極小值點呢？看以下這幅圖： 最下方的線是規則化之前的結構化風險函式，中間的是L2規則化的，最上面的是L1規則化的，圖片來自於（https://www.zhihu.com/question/37096933王贇 Maigo） 的回答。圖中的綠色、黃色、紅色的點分別表示這三種函式的極小值點。從圖中我們可以看出，只有L1正則的極小值點是在引數為0的位置的，那麼這個函式的特點自然是左右兩邊的導數正好是$\theta>0$時導數大於0，單調遞增，$\theta<0$時導數小於0，單調遞減，從這一點啟發，我們就可以重新回去看那個公式了，想要在$\theta=0$處獲得最小值，需要： $\frac{\partial L}{\partial \theta}+\lambda>0$ 且$\frac{\partial L}{\partial \theta}-\lambda<0$ 結合以上兩個式子我們得出，只要在$\theta=0$的位置滿足$\lambda>|\frac{\partial L}{\partial \theta}|$，我們就能獲得圖中粉色線的結果，在$\theta=0$的位置獲得極小值。

那麼L2正則呢？先看看導數： $\frac{\partial L2}{\partial \theta}= \frac{\partial L}{\partial \theta}+ 2\lambda \theta$ 很容易發現，當$\theta=0$的時候，L2的導數就是原來L的導數，所以原來的極小值不在$\theta=0$的位置，那麼L2規則化之後的也不會在這個位置。這就解釋了為什麼L1稀疏而L2不稀疏。

4、 直觀解釋

下面要放那張被詬病面試時被問死了的圖了，如下： 參考了（https://www.zhihu.com/question/37096933 這個問題下王小明的回答）。這裡只考慮了兩個引數的情況，等高線是怎麼畫出來的我在邏輯迴歸的詳解裡寫過了，本質就是所有樣本點的損失函式構成的代價函式是一個拋物面（兩個引數的情況下），這個拋物面的損失值取不同值的時候其在引數平面的投影就是這個等高線圖。

具體分析時，為什麼可以把結構化風險函式拆分成兩部分？因為在優化裡 和 是等價的問題。那麼通過$E_R(\omega)<=\eta$，我們也可以很清楚地知道圓和菱形是怎麼來的了，因為你限制了它們小於等於一個常數，那麼$|\omega_1|+|\omega_2|<=\eta$可不就是個菱形麼？$\omega_1^2+\omega_2^2<=\eta$可不就是個圓麼？也就是說我們原來要找的極小值點就是藍色等高線的最中心點，而現在我們需要在黃色區域內尋找在儘可能靠近等高線中心點的值。$\lambda$越大，$\eta$越小（這個數學解釋並不清楚，我只能直觀地理解它是為了滿足整體最小的約束），那麼黃色區域面積越小，等高線上獲得的極小值會越大，與原來的解相差越多，規則化作用也就越明顯。反之，如果$\lambda$非常小，那麼黃色區域會非常大，大到包含原始中心點時，規則化就不起任何作用了。

5、 參考資料