斯坦福cs231n計算機視覺——線性分類器(中 下),損失函式和最優化
week 2 10/15-10/21
損失函式和最優化:cs231n_2018_lecture03
觀看視訊 p7 和 p8,瞭解更多關於線性分類器,損失函式以及優化器的相關知識
損失函式 Loss function
我們將使用損失函式(Loss Function)(有時也叫代價函式Cost Function或目標函式Objective)來衡量我們對結果的不滿意程度。直觀地講,當評分函式輸出結果與真實結果之間差異越大,損失函式輸出越大,反之越小。
多類支援向量機損失 Multiclass Support Vector Machine Loss
SVM的損失函式想要正確分類類別的分數比不正確類別分數高,而且至少要高
正則化(Regularization):上面損失函式有一個問題。假設有一個數據集和一個權重集W能夠正確地分類每個資料(即所有的邊界都滿足,對於所有的i都有)。問題在於這個W並不唯一:可能有很多相似的W都能正確地分類所有的資料。
換句話說,我們希望能向某些特定的權重W新增一些偏好,對其他權重則不新增,以此來消除模糊性。這一點是能夠實現的,方法是向損失函式增加一個正則化懲罰(regularization penalty)部分。最常用的正則化懲罰是L2正規化,L2正規化通過對所有引數進行逐元素的平方懲罰來抑制大數值的權重:
完整公式如下所示:
將其展開完整公式是:
Softmax分類器
在Softmax分類器中,函式對映保持不變,但將這些評分值視為每個分類的未歸一化的對數概率,並且將折葉損失(hinge loss)替換為交叉熵損失(cross-entropy loss)。公式如下:
或等價的
SVM和Softmax的比較
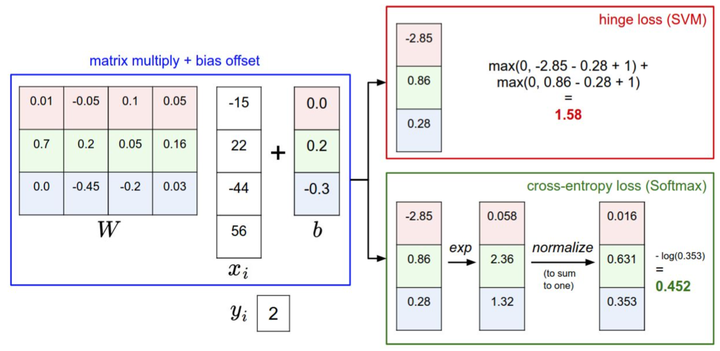
SVM當一個數據點超過閾值,它就放棄這個點了,不關心這個資料點。而Softmax總是試圖不斷提高,每一個數據點都會越來越好。這是兩個函式的差異。
而softmax分類器可以計算出這三個標籤的”可能性“是[0.9, 0.09, 0.01],這就讓你能看出對於不同分類準確性的把握。為什麼我們要在”可能性“上面打引號呢?這是因為可能性分佈的集中或離散程度是由正則化引數λ直接決定的,λ是你能直接控制的一個輸入引數。舉個例子,假設3個分類的原始分數是[1, -2, 0],那麼softmax函式就會計算:
現在,如果正則化引數λ更大,那麼權重W就會被懲罰的更多,然後他的權重數值就會更小。這樣算出來的分數也會更小,假設小了一半吧[0.5, -1, 0],那麼softmax函式的計算就是:
現在看起來,概率的分佈就更加分散了。還有,隨著正則化引數λ不斷增強,權重數值會越來越小,最後輸出的概率會接近於均勻分佈。這就是說,softmax分類器算出來的概率最好是看成一種對於分類正確性的自信。和SVM一樣,數字間相互比較得出的大小順序是可以解釋的,但其絕對值則難以直觀解釋。
最優化筆記上
我們可以通過數學公式來解釋損失函式的分段線性結構。對於一個單獨的資料,有損失函式的計算公式如下:
通過公式可見,每個樣本的資料損失值是以為引數的線性函式的總和(零閾值來源於
函式)。
的每一行(即
),有時候它前面是一個正號(比如當它對應錯誤分類的時候),有時候它前面是一個負號(比如當它是是正確分類的時候)。為進一步闡明,假設有一個簡單的資料集,其中包含有3個只有1個維度的點,資料集資料點有3個類別。那麼完整的無正則化SVM的損失值計算如下:
-->針對資料1,屬於類別1。
-->針對資料2,屬於類別2。
-->針對資料3,屬於類別3。
-->整個訓練集的平均損失函式。
因為這些例子都是一維的,所以資料和權重
都是數字。觀察
,可以看到上面的式子中一些項是
的線性函式,且每一項都會與0比較,取兩者的最大值。可作圖如下:——————————————————————————————————————
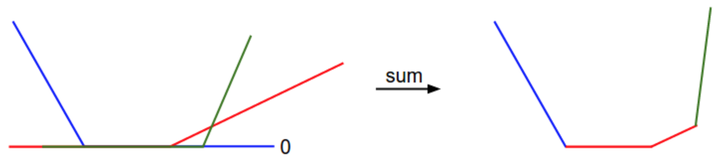
從一個維度方向上對資料損失值的展示。x軸方向就是一個權重,y軸就是損失值。資料損失是多個部分組合而成。其中每個部分要麼是某個權重的獨立部分,要麼是該權重的線性函式與0閾值的比較。你可能根據SVM的損失函式的碗狀外觀猜出它是一個凸函式。
不可導的損失函式。作為一個技術筆記,你要注意到:由於max操作,損失函式中存在一些不可導點(kinks),這些點使得損失函式不可微,因為在這些不可導點,梯度是沒有定義的。但是次梯度(subgradient)依然存在且常常被使用。在本課中,我們將交換使用次梯度和梯度兩個術語。
損失函式可以量化某個具體權重集W的質量。而最優化的目標就是找到能夠最小化損失函式值的W 。我們現在就朝著這個目標前進,實現一個能夠最優化損失函式的方法。對於有一些經驗的同學,這節課看起來有點奇怪,因為使用的例子(SVM 損失函式)是一個凸函式問題。但是要記得,最終的目標是不僅僅對凸函式做最優化,而是能夠最優化一個神經網路,而對於神經網路是不能簡單的使用凸函式的最優化技巧的。
策略#1:一個差勁的初始方案:隨機搜尋
即遍歷法,嘗試不同的w,選擇最小的一個。
策略#2:隨機本地搜尋
每走一步前,嘗試幾個方向,選最最小方向走
策略#3:跟隨梯度
作業:
