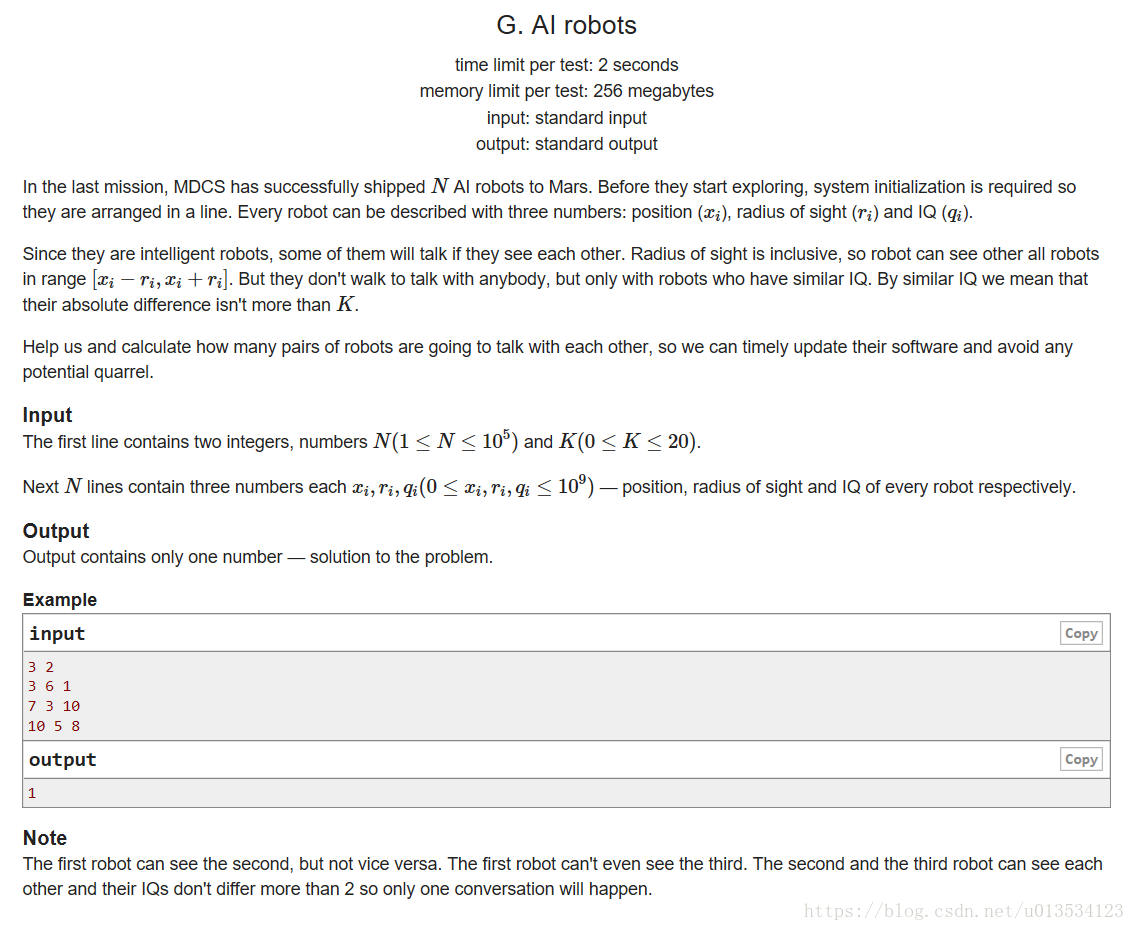
CodeForces 1045G AI robots(CDQ分治 + 樹狀陣列 + 單調佇列)
大致題意:有很多個機器人,他們要相互交流有一些限制條件。首先是,兩個人要相互能夠能夠看到;其次,兩個人的智商的差不超過K。現在給出每個機器人的視力範圍和他們的智商,現在問你總共有多少對機器人能夠相互交流。
首先來看下總共有多少個限制條件。由於是要求雙方都能夠看到,所以顯然是要按照視野半徑去排序的。然後要求兩個人的智商差要在一定的範圍內的,所以也要按照智商去排序。另外還要跟自己的位置有關。根據這個,我們可以構造出分治的大致方法:首先按照半徑去排序,半徑大的在前面,因為這樣如果後面的東西能夠看到前面,那麼前面的東西一定能看到後面,符合cdq分治前面更新後面的要求;然後分治的過程中歸併排序按照智商的大小去排序,因為這樣可以利用一些單調性,同時好確定智商差;最後就是用一個離散化的樹狀陣列去維護每個位置的機器人數量。
前面和最後的都好說,關鍵是如何利用智商差去求能夠相互看到的機器人的對數。這裡我們用到了單調佇列。由於是按照智商的大小來進行分治的。所以前一半和後一半已經是按照智商的大小排好序了的,所以說我們可以利用單調性。根據cdq分治的原則,前面一半去更新後面一半,所以我們考慮對於後一半的每個機器人,單獨計算貢獻。對於後一半的第i個機器人,我可以在前一半確定一個區間[j,k],在這個區間內的所有機器人與機器人i的智商差不超過K。把這個區間內的所有機器人新增到樹狀陣列中,然後貢獻就是機器人i視野範圍內的機器人數目。然後再往後考慮後一半的其他機器人。由於前一半和後一半的智商是遞減的,所以從i移動到i+1區間的移動只會單調往後移動,符合單調佇列性質。這樣前一半的每一個機器人只會進出佇列各一次,對應加入和移出樹狀陣列各一次。所以這個部分均攤的時間複雜度是O(NlogN)的,這個log來自樹狀陣列。
如此我們就求出了合併的時候前面對後面產生的貢獻。總的時間複雜度就是O(NlogNlogN)。具體見程式碼:
#include<bits/stdc++.h> #define LL long long #define N 100010 using namespace std; struct node{int x,r,iq,L,R;} p[N],tmp[N]; int n,tot,K,x[N<<2],q[N]; LL ans=0; struct BinaryIndexedTree { int c[N<<2]; inline void update(int x,int k) { x=min(x,tot); for(;x<=tot;x+=x&-x) c[x]+=k; } inline int getsum(int x) { int ans=0; for(;x>0;x-=x&-x) ans+=c[x]; return ans; } } BIT; bool cmp1(node a,node b) { return a.r>b.r; } bool cmp2(node a,node b) { return a.iq>b.iq; } void cdq(int l,int r) { if (l==r) return; int mid=(l+r)>>1; cdq(l,mid); cdq(mid+1,r); int h=0,t=0; for(int i=mid+1,j=l;i<=r;i++) { while(j<=mid&&p[j].iq-p[i].iq>K) j++; while(j<=mid&&abs(p[j].iq-p[i].iq)<=K) { BIT.update(p[j].x,1); q[t++]=j++; } while(h<t&&abs(p[q[h]].iq-p[i].iq)>K) { BIT.update(p[q[h]].x,-1); h++; } ans+=BIT.getsum(p[i].R)-BIT.getsum(p[i].L-1); } for(;h<t;h++) BIT.update(p[q[h]].x,-1); inplace_merge(p+l,p+mid+1,p+r+1,cmp2); } int main() { scanf("%d%d",&n,&K); for(int i=1;i<=n;i++) { int X,Y,Z; scanf("%d%d%d",&X,&Y,&Z); p[i]=node{X,Y,Z,0,0}; x[++tot]=X; x[++tot]=X-Y; x[++tot]=X+Y; } sort(x+1,x+tot+1); tot=unique(x+1,x+tot+1)-x-1; for(int i=1;i<=n;i++) { p[i].L=lower_bound(x+1,x+tot+1,p[i].x-p[i].r)-x; p[i].R=lower_bound(x+1,x+tot+1,p[i].x+p[i].r)-x; p[i].x=lower_bound(x+1,x+tot+1,p[i].x)-x; } sort(p+1,p+n+1,cmp1); cdq(1,n); printf("%lld\n",ans); return 0; }