三大抽樣分佈:卡方分佈,t分佈和F分佈的簡單理解
有很多統計推斷是基於正態分佈的假設,以標準正態分佈變數為基石而構造的三個著名統計量在實際中有廣泛的應用,這是因為這三個統計量不僅有明確背景,而且其抽樣分佈的密度函式有顯式表示式,它們被稱為統計中的“三大抽樣分佈”。這三大抽樣分佈即為著名的卡方分佈,t分佈和F分佈。
目錄
1 卡方分佈(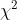 分佈)
分佈)
1.1 定義
設隨機變數 X 是自由度為 n 的 χ2 隨機變數, 則其概率密度函式為
表示的是一個gamma函式,它是整數k的封閉形式。gamma函式的介紹如下
的密度函式
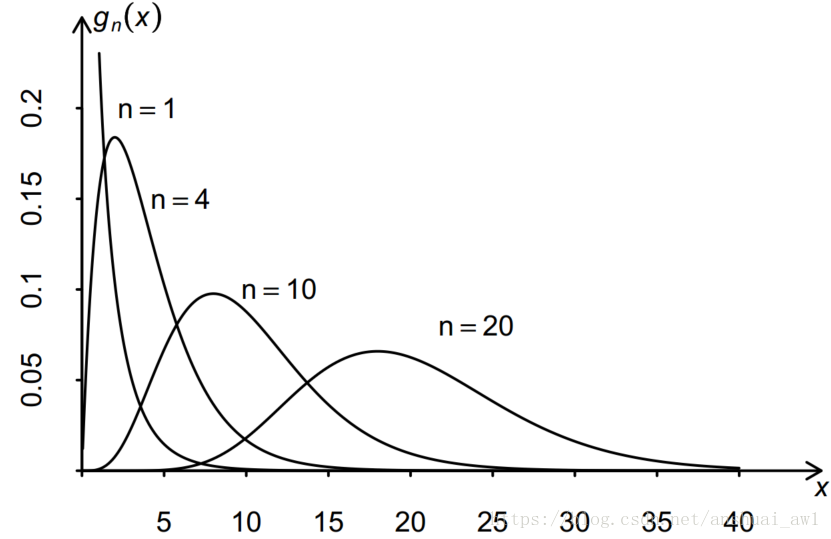
形狀如下圖
密度函式的支撐集 (即使密度函式為正的自變數的集合) 為(0, +∞), 從上圖可見當自由度 n 越大,
的密度曲線越趨於對稱, n
越小, 曲線越不對稱. 當 n = 1, 2 時曲線是單調下降趨於 0. 當 n ≥ 3時曲線有單峰, 從 0 開始先單調上升, 在一定位置達到峰值, 然後單下降趨向於 0。
若 X ∼ , 記
,則
稱為
分佈的上側
分位數, 如下圖所示。當
和
給定時可查表求出
之值,如
,
等。
1.2 性質
χ2 變數具有下列性質:
2 t分佈
說起t分佈,首先要提一句u分佈,正態分佈(normal distribution)是許多統計方法的理論基礎。正態分佈的兩個引數μ和σ決定了正態分佈的位置和形態。為了應用方便,常將一般的正態變數X通過u
由於在實際工作中,往往σ(總體方差)是未知的,常用s(樣本方差)作為σ的估計值,為了與u變換區別,稱為t變換,統計量t 值的分佈稱為t分佈。
2.1 定義
設隨機變數 T ∼ , 則其密度函式為
該密度函式的圖形如下
的密度函式與標準正態分佈 N(0, 1) 密度很相似, 它們都是關於原點對稱, 單峰偶函式, 在 x = 0 處達到極大. 但
的峰值低於
N(0, 1) 的峰值, 的密度函式尾部都要比 N(0, 1) 的兩側尾部粗一些. 容易證明:
此處 是 N(0, 1) 變數的密度函式。
若T ∼ ,記
,則
為自由度為n的t分佈的雙側
分位數(如上圖所示). 當給定
時,
,
等可通過查表求出. 例如 ,
等。
t 分佈是英國統計學家 W.S. Gosset 在 1908 年以筆名 Student發表的論文中提出的, 故後人稱為 “學生氏 (Student) 分佈” 或 “t 分
布”。
2.2 性質
t 變數具有下列的性質:
3 F分佈
3.1 定義
若隨機變數 Z ∼, 則其密度函式為
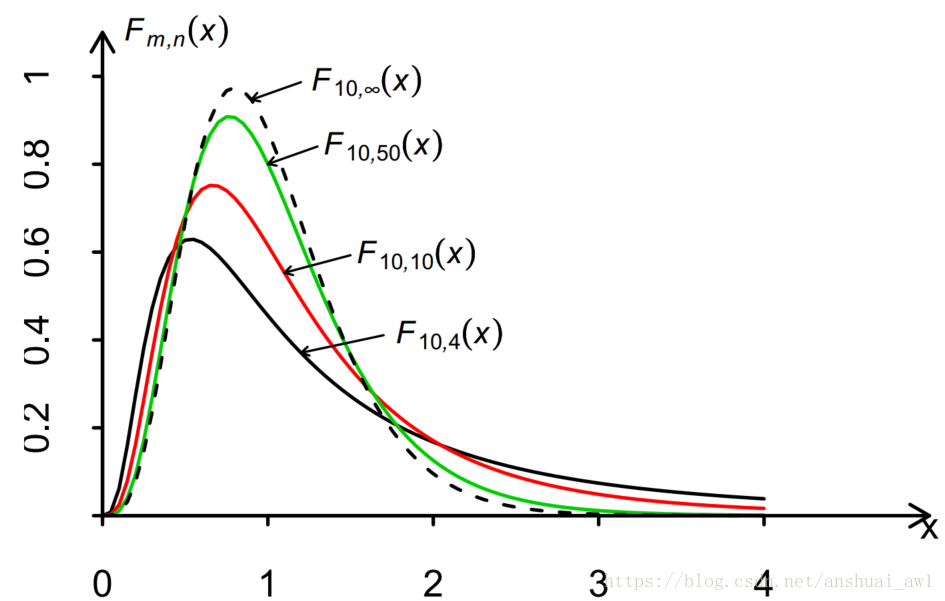
自由度為 m, n 的 F 分佈的密度函式如下圖:
注意 F 分佈的自由度 m 和 n 是有順序的, 當 時, 若將自由度 m 和 n 的順序顛倒一下, 得到的是兩個不同的 F 分佈. 從上圖
可見對給定 m = 10, n 取不同值時 的形狀, 我們看到曲線是偏態的, n 越小偏態越嚴重。
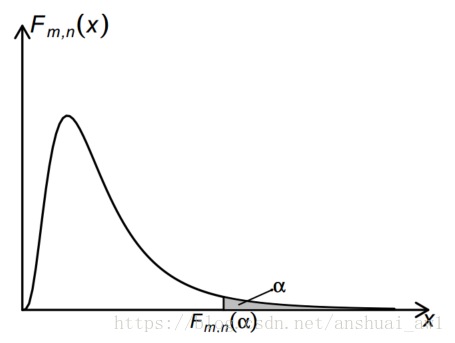
若 F ∼ , 記
, 則
稱為 F 分佈的上側
分位數 (見上圖). 當 m, n 和
給定時, 可以通過查表求出
之值, 例如
,
等. 在區間估計和假設檢驗問題中常常用到.
3.2 性質
F 變數具有下列的性質:
以上性質中 (1) 和 (2) 是顯然的, (3) 的證明不難. 尤其性質 (3)在求區間估計和假設檢驗問題時會常常用到. 因為當 α 為較小的數,
如 α = 0.05 或 α = 0.01, m, n 給定時, 從已有的 F 分佈表上查不到 和
之值, 但它們的值可利用性質(3) 求得, 因為
和
是可以通過查 F 分佈表求得的.
4 正態總體樣本均值和樣本方差的分佈
為方便討論正態總體樣本均值和樣本方差的分佈, 我們先給出正態隨機變數的線性函式的分佈.
4.1 正態變數線性函式的分佈

4.2 正態變數樣本均值和樣本方差的分佈
下述定理給出了正態變數樣本均值和樣本方差的分佈和它們的獨立性.
5 幾個重要推論
下面幾個推論在正態總體區間估計和假設檢驗問題中有著重要應用.
6 總結
資料在使用前要注意採用有效的方法收集資料, 如設計好抽樣方案, 安排好試驗等等. 只有有效的收集了資料, 才能有效地使用資料,開展統計推斷工作.獲得資料後, 根據問題的特點和抽樣方式確定抽樣分佈, 即統計模型. 基於統計模型, 統計推斷問題可以按照如下的步驟進行:
- 確定用於統計推斷的合適統計量;
- 尋求統計量的精確分佈; 在統計量的精確分佈難以求出的情形,可考慮利用中心極限定理或其它極限定理找出統計量的極限分佈.
- 基於該統計量的精確分佈或極限分佈, 求出統計推斷問題的精確解或近似解.
- 根據統計推斷結果對問題作出解釋
其中第二步是最重要, 但也是最困難的一步. 統計三大分佈及正態總體下樣本均值和樣本方差的分佈, 在尋求與正態變數有關的統計量精確分佈時, 起著十分重要作用. 尤其在求區間估計和假設檢驗問題時可以看得十分清楚