題解正文

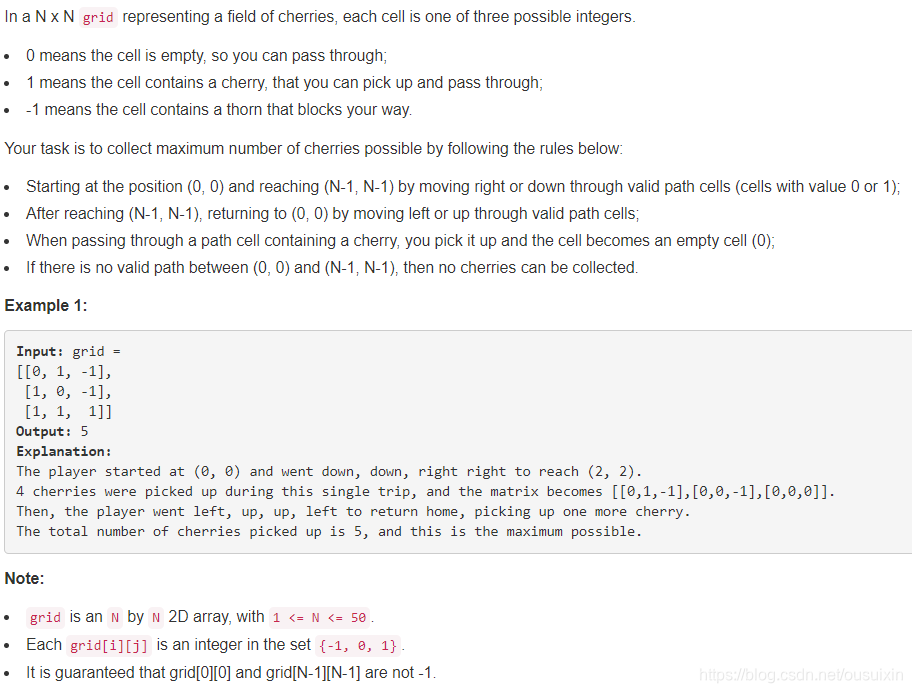
題目描述

問題分析

此題給出一個n乘n矩陣，矩陣中值可以是0/1/-1。
要求我們找出從（0，0）出發，到（n-1，n-1），然後回到（0，0）的路徑，要求往程只能向右向下，而返程只能向左向上走，並且路徑沒有經過值為-1的位置。
然後求出符合上述要求的路徑中，所經過的所有位置值加和最大的路徑，將其經過的各個位置值加和，作為答案返回。

思路分析

這周本來先做了leetcode的Dungeon Game這個題，標籤是hard，但是感覺並不很難，所有繼續往下做直到做到這個題，我一看題目覺得這兩個題目不就是同一個題目嗎，只不過Dungeon Game只需要針對單程求解問題，而

Cherry Pickup這道題需要先求出最大的往程節點值之和，然後將往程經過的路徑上的值設為0，然後求出最大的返程節點值之和，將兩個最大加起來就是答案。但是這個做法遇到了一個問題，遇到下面的例子會出現問題：
1 1 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 1
1 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 1 1 1
在這個例子中，按照我們原本的演算法，會得出如下往程和返程（加粗表示）：
1 1 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 1
1 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 1 1 1
或者
1 1 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 1
1 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 1 1 1
還有其它選擇方法，但是往程都一樣，只是返程所選擇的路徑會經過（2，6）和（0，3）其中一個，因此往返經過路徑的節點值加起來是13+1 = 14（注意重疊的點只能算一次加法）
但是實際上最優路徑如下：
1 1 1 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 1
1 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 0 0 0
0 0 0 1 1 1 1
當然還有其它走法，總之都可以經過（2，6）和（0，3）這兩個點，而不是其中一個，所以往返經過路徑的節點值加起來是8+7 = 14（注意重疊的點只能算一次加法）
相比最優解我們的答案不正確，這是因為分為子問題取最優然後合併子問題，並不等價於整個問題取最優。所以我們需要從整體考慮，而不能夠分往返程求解然後合併。

其實稍加思考我們就知道，往返路徑合起來也可以看成是，兩條單程路徑放在一起，所以問題變成求解兩條往程路經過徑節點值求和最大是多少，如果換一個角度分析問題，問題可以進一步變成：兩個人同時以v=1的速度從（0，0）去往（n-1，n-1），經過t=2n-1之後，兩個人將同時到達終點，求出他們路經節點值之和最大值，如果兩人都經過了某個相同的節點，那麼該節點值只能被加一次。
要解決上述問題，我們需要更加詳細的分析兩個人的行進過程：假設在出發後的t時刻，第一個人所在位置橫座標x1，那麼此人座標為（x1，t-x1），同理假設第二個人所在位置橫座標x2，那麼此人座標為（x2，t-x2），那麼我們可以使用元組（t，x1，x2）來唯一標識一個進行過程狀態，用maxSum（t，x1，x2）來表示當前狀態下他們已經經過節點的節點值之和（同一個節點只能加一次），而maxSum陣列的計算方法就是本題求解的核心。
假設現在在t時刻，我們目前已經知道了t時刻之前所有的maxSum（i，j，k）了（i<t，x1<n，x2<n），我們要求解maxSum（t，x1<n，x2<n）這個陣列，我們可以遍歷每個maxSum（t，x1，x2），這個數值對應的狀態用（t，x1，x2）的前一個狀態可以有四種可能：（t-1，x1，x2）、（t-1，x1-1，x2）、（t-1，x1，x2-1）、（t-1，x1-1，x2-1），即他們可以且僅可以從這四個狀態經過一個時間單位到達（t，x1，x2），其它狀態是不能經過一個時間單位就到達（t，x1，x2）狀態的，如下圖所示：

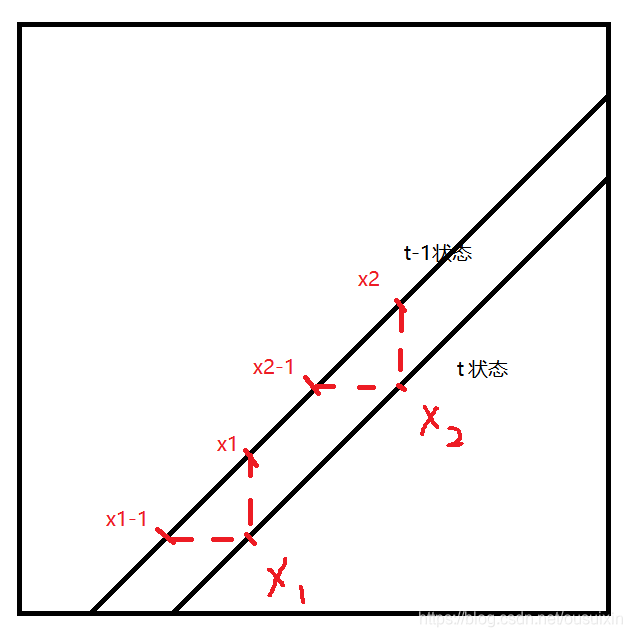
所以我們求解maxSum（t，x1，x2）的時候，求出maxSum（t-1，x1，x2）、maxSum（t-1，x1-1，x2）、maxSum（t-1，x1，x2-1）、maxSum（t-1，x1-1，x2-1）的最大值，再加上（x1，t-x1），（x2，t-x2）這兩個節點本身的數值即可（如果兩個節點重合則只需要加一次），但是如果（x1，t-x1），（x2，t-x2）中有一個節點值為-1那麼這個走法不可行（因為這個節點不能走），需要設定maxSum（t，x1，x2）為-1，或者maxSum（t-1，x1，x2）、maxSum（t-1，x1-1，x2）、maxSum（t-1，x1，x2-1）、maxSum（t-1，x1-1，x2-1）的最大值為-1，那麼這個走法也不可行（因為沒有任何一個可行狀態能夠經過一個時間單位到達改狀態）
最後，當我們完成對maxSum（t，x1<n，x2<n）這個陣列的遍歷之後，我們再繼續完成對maxSum（t+1，x1<n，x2<n）、maxSum（t+1，x1<n，x2<n）等陣列的求解，直到我們完成對整個maxSum（t<2n-1，x1<n，x2<n）陣列的遍歷，我們知道本問題答案就是經過時間2n-1之後，兩個人都到達（n-1，n-1）這一點，即x1 == x2 == n-1，此時maxSum的值，然後在maxSum[2n-2][n-1][n-1]這個對應位置找到本問題的答案。

最後我們還可以對於正確解法做一下優化：本來我們需要的空間複雜度是n立方，也就是需要一個maxSum（t<2n-1，x1<n，x2<n）三維陣列，但是其實我們只使用maxSum（x1<n，x2<n）也能完成任務，這需要我們在對maxSum（t，x1<n，x2<n）這個陣列的遍歷的時候，先算x1，x2比較大的狀態，然後算x1，x2比較小的狀態。因為maxSum（i，x1，x2）在求解的時候取決於maxSum（i-1，x<=x1，x’<=x2），我們使用反向求解能夠保證修改maxSum（x<=x1，x’<=x2）之後，maxSum（x<=x1，x’<=x2）中的值不再被使用，從而安全完成問題求解，之所以不會在修改之後使用，是因為，需要用到maxSum（x<=x1，x’<=x2）的那些狀態的x1，x2下標更大，而具有更大x1，x2下標的狀態在反向求解之中已經被先行求解了。
最終通過這種做法大大優化了空間複雜度。更多細節見程式碼實現

演算法實現

初始化陣列maxCherries為全-1；

設定maxCherries[0][0]為0；

遍歷t∈（0，2n-1），每一輪求解一次陣列maxCherries（x1<n，x2<n），即求解經過時間t，兩人所能到達的全部狀態對應的節點值之和：
	遍歷x1∈（0，n-1），每一輪固定x1求解陣列maxCherries（x1，x2<n），即第一個人經過t走到的位置，求解第二個人所能達到的全部狀態對應的節點值之和：
		遍歷x2∈（0，n-1），每一次求解經過時間t之後，第一個人到達x1，第二個人到達x2時對應的路徑上節點值之和，即maxCherries（x1，x2）：
			如果（x1，t-x1），（x2，t-x2）中有一個節點值為-1：
				設定maxCherries（t，x1，x2）為-1；
				跳出該次迴圈，x2++，進入下一次迴圈；
				
			求解maxCherries（t-1，x1，x2）、maxCherries（t-1，x1-1，x2）、maxCherries（t-1，x1，x2-1）、maxCherries（t-1，x1-1，x2-1）的最大值，記為temp；
			
			如果temp為-1：
				設定maxCherries（t，x1，x2）為-1；
				跳出該次迴圈，x2++，進入下一次迴圈；
			否則：
				如果兩個節點（x1，t-x1），（x2，t-x2）重合則：
					設定maxCherries（t，x1，x2）為temp+矩陣在（x1，t-x1）的數值+矩陣在（x2，t-x2）的數值；
				否則：
					設定maxCherries（t，x1，x2）為temp+矩陣在（x1，t-x1）的數值；

返回maxCherries[n-1][n-1]和0中的最大值作為本題答案；

複雜度分析

時間複雜度：主要部分就是對於陣列maxSum（x1<n，x2<n）的動態規劃求解，這個求解需要2n-1輪，每一輪需要nn（常數）的時間複雜度，所以該演算法總共的時間複雜度是 $O(n^3)$，其它過程沒有超過該過程複雜度的，所以最終複雜度就是n立方。
空間複雜度：通過優化你，我們最終僅僅使用了陣列maxSum（x1<n，x2<n）就完成了問題求解，所以空間複雜度是 $O(n^2)$，其他都是迴圈遍歷用到的臨時變數，三層迴圈需要平方個臨時變數，因此總共的空間複雜度還是 $O(n^2)$

程式碼實現&結果分析：

程式碼實現：

class Solution {
public:
    int cherryPickup(vector<vector<int>>& nums) {
    	int n = nums.size();
    	vector<vector<int>> maxCherries(n, vector<int>(n, -1));
    	maxCherries[0][0] = nums[0][0];
    	for (int t = 1; t <= 2*n-1; t++) {
    		for (int x1 = min(t, n-1); x1 >= max(0, t-(n-1)); --x1) {
    			for (int x2 = min(t, n-1); x2 >= max(0, t-(n-1)); --x2)	{
    				if (nums[x1][t-x1] == -1 || nums[x2][t-x2] == -1) {
    					maxCherries[x1][x2] = -1;
    					continue;
    				}
    				if (x1 > 0) {
    					maxCherries[x1][x2] = max(maxCherries[x1][x2], maxCherries[x1-1][x2]);
    				}
    				if (x2 > 0) {
    					maxCherries[x1][x2] = max(maxCherries[x1][x2], maxCherries[x1][x2-1]);
    				}
    				if (x1 > 0 && x2 > 0) {
    					maxCherries[x1][x2] = max(maxCherries[x1][x2], maxCherries[x1-1][x2-1]);
    				}
    				if (maxCherries[x1][x2] == -1) {
    					continue;
    				}
    				maxCherries[x1][x2] = maxCherries[x1][x2] + nums[x1][t-x1] + (x1 == x2 ? 0 : nums[x2][t-x2]);
    			}
    		}
    	}
    	return max(0, maxCherries[n-1][n-1]);
    }
};

提交結果：從結果看來，經過優化後的演算法無論從時間還是空間複雜度看都是相當好了。