六天搞懂“深度學習”之二:神經網路
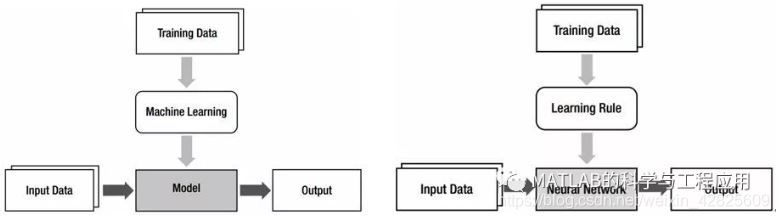
注意對比左右兩個框圖,用神經網路代替模型,用學習規則代替機器學習。
因此,神經網路是實現機器學習的一種重要模型,確定模型(神經網路)的過程稱為學習規則。
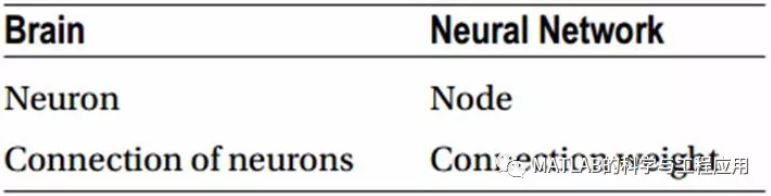
大腦與神經網路的類比:大腦的神經元對應神經網路的節點,大腦的神經元連線對應神經網路的連線權值。
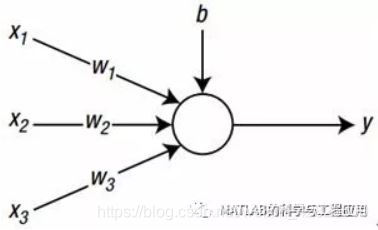
三輸入的神經網路節點示意圖,其中x1、x2、x3為輸入訊號,w1、w2、w3為對應x1、x2、x3的權值,b為偏置,y為神經網路節點的輸出。也就是說,神經網路的資訊以權值和偏置的形式儲存。三輸入神經網路節點的計算如下:
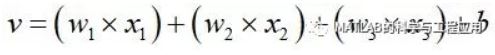
如果權值w1=1,w2=5,那麼訊號x2產生的效果將比x1大5倍;當w1=0,則表明訊號x1並不對節點發送任何資訊。節點將加權和v輸入啟用函式φ得到:
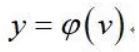
啟用函式決定了節點的行為。
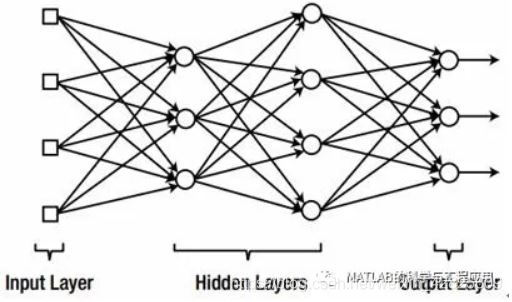
神經網路的分層結構示意圖:輸入層、隱藏層、輸出層。只有輸入和輸出層的神經網路,稱為單層神經網路。
包含兩個或多個隱藏層的多層神經網路被稱為深度神經網路。在實際應用中使用的大多數神經網路都是深度神經網路。

節點的啟用函式為線性函式示例,但是這種啟用函式並不實用,節點中線性函式的使用否定了隱藏層的作用效果。(因為y = x不涉及任何變換)在這種情況下,該模型在數學上與單層神經網路相同,該神經網路不具有隱藏層。
增量規則是一種神經網路的學習規則,也被稱為Adaline規則或者Widrow-Hoff規則。增量規則是一種稱為梯度下降的數值方法。
單層神經網路的增量規則訓練過程如下:
-
以適當的值初始化權值。(權值的初始化可以是隨機的,也可以是預先優化的,或者是經驗值) -
從{輸入、正確輸出}的訓練資料中提取“輸入”資料,並將其輸入神經網路。計算神經網路的輸出yi與輸入對應的正確輸出di之間的誤差。
ei= di - yi
-
根據以下增量規則計算權值更新:
Δwij = αeixj
-
調整權值:
wij= wij + Δwij
-
對所有訓練資料執行第2 – 4步。 -
重複第2 – 5步,直到誤差達到可接受的水平。
每訓練迭代一次,所有訓練資料都將步驟2 – 5執行一次,該過程也稱為紀元或時代。(epoch)
對於任意啟用函式,增量規則可表示為:
wij = wij + αδixj
其中δi=φ’(vi)ei,φ’為輸出節點i的啟用函式的導數。當啟用函式為線性函式時,啟用函式的導數為1。
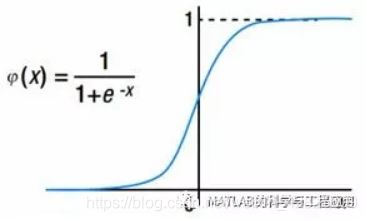
廣泛使用的啟用函式:sigmoid函式。sigmoid函式的輸出值範圍為0 – 1之間,當神經網路產生概率輸出時,sigmoid函式的這種行為是很有用的。
神經網路的有監督學習實現權值更新一般有三種典型方案:隨機梯度下降(Stochastic Gradient Descent,SGD)、批處理(Batch)、小批量處理(Mini batch)。
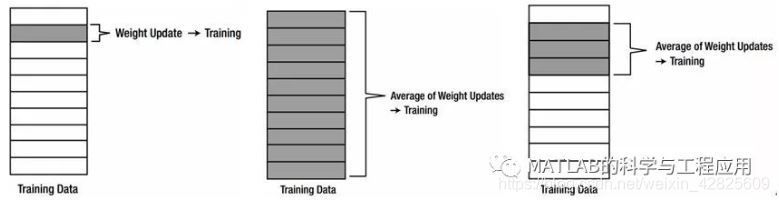
上圖從左到右為:隨機梯度下降、批處理、小批量處理
如果我們有100個訓練資料點,SGD將調整權值100次。在批處理中,由於平均加權更新的計算,批處理方法需要消耗大量的時間進行訓練。為了降低批處理的計算量,小批量處理選擇出訓練資料中的一部分用於批量處理訓練,當選擇合適的處理資料規模時,小批量處理方法會獲得SGD的收斂速度和批處理的穩定性。因此,在深度學習處理海量資料時,小批量處理方法經常被實際應用。
批處理方法中運用的平均特性使得訓練過程相對於訓練資料的敏感程度降低。批處理方法需要更多的時間來訓練神經網路,以產生與SGD方法類似的精度水平,但批處理的優點是:收斂穩定性好。
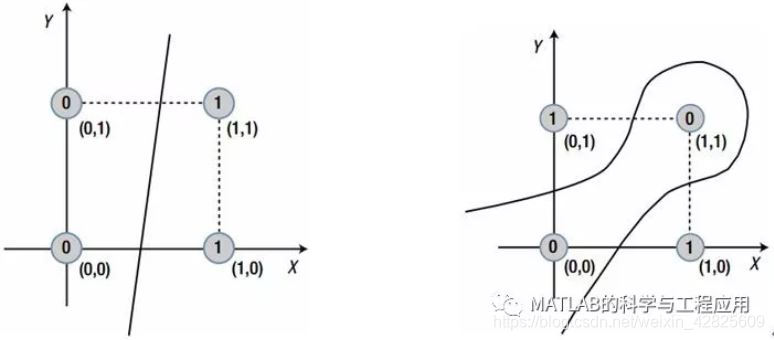
以上圓圈中標為“0”的資料為一組,標為“1”的資料為另一組,左圖為線性可分的兩組資料,右圖無法用直線區分兩組資料,必須用曲線進行分組
單層神經網路只能解決左圖中的線性可分問題。為了克服單層神經網路的本質侷限性,必須研究更復雜的多層神經網路。
更多精彩文章請關注微訊號:
