分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow

也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！

               

1、8*8的棋盤上面放著64個不同價值的禮物，每個小的棋盤上面放置一個禮物（禮物的價值大於0），一個人初始位置在棋盤的左上角，每次他只能向下或向右移動一步，並拿走對應棋盤上的禮物，結束位置在棋盤的右下角，請設計一個演算法使其能夠獲得最大價值的禮物。

//經典的動態規劃//dp[i][j] 表示到棋盤位置（i，j）上可以得到的最大禮物值//dp[i][j] = max( dp[i][j-1] , dp[i-1][j] ) + value[i][j]  （0<i，j<n）int i, j, n = 8;dp[0][0] = value[0][0];for( i = 1 ; i < n ; i++ ){ dp[i][0] = dp[i-1][0] + value[i][0];}for( j = 1 ; j < n ; j++ ){ dp[0][j] = dp[0][j-1] + value[0][j];}for( i = 1
 
 ; i < n ; i++ ){ for( j = 1 ; j < n ; j++ ) {  dp[i][j] = max( dp[i][j-1] , dp[i-1][j] ) + value[i][j]; }}cout<<dp[n-1][n-1]<<endl;

擴充套件：現在增加一個限定值limit，從棋盤的左上角移動到右下角的時候的，每次他只能向下或向右移動一步，並拿走對應棋盤上的禮物，但是拿到的所有的禮物的價值之和不大於limit，請設計一個演算法請實現。

int row,col;int limit;int
 
 dp[row][col][limit];int getMaxLessLimit(){ memset(dp,0,sizeof(dp)); for(int r = row-1 ; r >= 0; r--) {  for(int c = col-1 ; c >= 0; c--)  {   for(int l = 0 ; l <= limit; l++)   {    if(l >= matrix[r][c])    {     int max = 0;     if(r != row-1 && dp[r+1][c][l-matrix[r][c]]>max)      max = dp[r+1][c][l-matrix[r][c]];     if(c != col-1 && dp[r][c+1][l-matrix[r][c]]>max)      max = dp[r][c+1][l-matrix[r][c]];     if(max == 0 && !(r == row-1 && c == col-1))      dp[r][c][l] = 0;     else      dp[r][c][l] = max + matrix[r][c];    }   }  } } return dp[0][0][limit];}

或者

int hash[row][col][limit];int getMaxLessLimit(){ memset(hash,0,sizeof(hash)); hash[0][0][matrix[0][0]] = 1; for(int i = 0 ; i < row ; i++) {  for(int j = 0 ; j < col ; j++)  {   for(int k = 0 ; k <= limit ; k++)   {    if(k >= matrix[i][j])    {     if(i >= 1 && hash[i-1][j][k-matrix[i][j]])      hash[i][j][k] = 1;     if(j >= 1 && hash[i][j-1][k-matrix[i][j]])      hash[i][j][k] = 1;    }   }  } } int ans = 0; for(int k = limit; k >= 0; k--) {  if(hash[row-1][col-1][k] && k>ans)   ans = k; } return ans;}

2、有兩個字串s1和s2，其長度分別為l1和l2，將字串s1插入到字串s2中，可以插入到字串s2的第一個字元的前面或者最後一個字元的後面，對於任意兩個字串s1和s2，判斷s1插入到s2中後是否能夠構成迴文串。。

3、已知有m個頂點，相鄰的兩個頂點之間有一條邊相連線，首尾頂點也有一條邊連線，這樣就構成了一個圓環。
現在有一個二維陣列M[][]，M[i][j]=1時，表明第i和j個節點之間有條邊存在，M[i][j]=0時，表明第i和j個節點之間沒有邊存在，其中 M[i][i]=0，M[i][j]=M[j][i]，輸入為一個二維陣列M[][]和頂點的個數n，試著判斷該圖中是否存在兩個圓環，且兩個圓環彼此之間沒有公共點。試著實現下面這個函式：
bool IsTwoCircle(int **M,int n)
{
  ......
}

4、給定如下的n*n的數字矩陣，每行從左到右是嚴格遞增， 每列的資料也是嚴格遞增

1 3 7 15 16

2 5 8 18 19

4 6 9 22 23
10 13 17 24 28
20 21 25 26 33
現在要求設計一個演算法， 給定一個數k 判斷出k是否在這個矩陣中。 描述演算法並且給出時間複雜度（不考慮載入矩陣的消耗）
方法一
從右上角開始（從左下角開始也是一樣的），然後每步往左或往下走。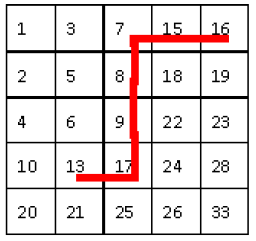

這樣每步都能扔掉一行或者一列，最壞的情況是被查詢的元素位於另一個對角，需要2N步，因此這個演算法是o(n)的，而且程式碼簡潔直接。

bool stepWise(int mat[][N] , int key , int &row , int &col){ if(key < mat[0][0] || key > mat[N-1][N-1])  return false; row = 0; col = N-1; while(row < N && col >= 0) {  if(mat[row][col] == key )     //查詢成功   return true;  else if(mat[row][col] < key )   ++row;  else   --col; } return false;}

方法二（分治法）
首先，我們注意到矩陣中的元素總是把整個矩陣分成四個更小的矩陣。例如，中間的元素9把整個矩陣分成如下圖所示的四塊。由於四個小矩陣也是行列有序的，問題自然而然地劃分為四個子問題。每次我們都能排除掉四個中的一個子問題。假如我們的查詢目標是21，21>9，於是我們可以立即排除掉9左上方的那塊，因為那個象限的元素都小於或等於9。

以下是這種二維二分的程式碼，矩陣的維度使用l、u、r、d刻畫的，其中l和u表示左上角的列和行，r和d表示右下角的列和行。

bool quadPart(int mat[][N] , int key , int l , int u , int r , int d , int &row , int &col){ if(l > r || u > d)  return false; if(key < mat[u][l] || key > mat[d][r])  return false; int mid_col = (l+r)>>1; int mid_row = (u+d)>>1; if(mat[mid_row][mid_col] == key)     //查詢成功 {  row = mid_row;  col = mid_col;  return true; } else if(l == r && u == d)  return false; if(mat[mid_row][mid_col] > key) {   // 分別在右上角、左上角、左下角中查詢  return quadPart(mat , key , mid_col+1 , u , r , mid_row , row , col) ||         quadPart(mat , key , l , mid_row+1 , mid_col , d , row , col) ||      quadPart(mat , key , l , u , mid_col , mid_row , row , col) ; } else {   // 分別在右上角、左下角、右下角中查詢  return quadPart(mat , key , mid_col+1 , u , r , mid_row , row , col) ||         quadPart(mat , key , l , mid_row+1 , mid_col , d , row , col) ||      quadPart(mat , key , mid_col+1 , mid_row+1 , r , d , row , col) ; }}bool quadPart(int mat[][N] , int key , int &row , int &col){ return bool quadPart(mat , key , 0 , 0 , N-1 , N-1 , row , col);}

5、設 一個64位整型n,各個bit位是1的個數為a個. 比如7, 2進位制就是 111, 所以a為3。

現在給出m個數, 求各個a的值。要求程式碼實現。

思路：如果可以直接用stl的bitset。演算法可用移位和&1來做。還有一個更好的演算法是直接位與（x-1)直到它為0。

while(n){ n = n & (n-1); ++count;}

6、有N＋2個數，N個數出現了偶數次，2個數出現了奇數次（這兩個數不相等），問用O（1）的空間複雜度，找出這兩個數，不需要知道具體位置，只需要知道這兩個值。
       求解：如果只有一個數出現過奇數次，這個就比較好求解了，直接將陣列中的元素進行異或，異或的結果就是隻出現過奇數次的那個數。
      但是題目中有2個數出現了奇數次？，求解方法如下：
      假設這兩個數為a，b，將陣列中所有元素異或結果x=a^b，判斷x中位為1的位數（注：因為a！=b，所以x！=0，我們只需知道某一個位為1的位數k，例如0010 1100，我們可取k=2或者3，或者5），然後將x與陣列中第k位為1的數進行異或，異或結果就是a，b中一個，然後用x異或，就可以求出另外一個。
      為什麼呢？因為x中第k位為1表示a或b中有一個數的第k位也為1，假設為a，我們將x與陣列中第k位為1的數進行異或時，也就是將x與a外加上其他第k位為1的出現過偶數次的數進行異或，化簡即為x與a異或，結果是b。
     程式碼如下：

void getNum(int a[],int length){ int s = 0;//儲存異或結果 for(int i=0;i<length;i++) {  s=s^a[i]; } int temp1 = s;     //臨時儲存異或結果 int temp2 = s;     //臨時儲存異或結果 int k=0; while((temp1&1) == 0)        //求異或結果中位為1的位數 {  temp1 = temp1>>1;  k++; } for(int i=0;i<length;i++) {  if((a[i]>>k)&1)          //將s與陣列中第k位為1的數進行異或，求得其中一個數  {   //cout<<a[i]<<" ";   s=s^a[i];  } } cout<<s<<" "<<(s^temp2)<<endl;             //(s^temp2)用來求另外一個數}

7、找出陣列中只出現一次的3個數。

思路類似於求解上題，關鍵是找出第一個來，然後藉助上題結論求另外兩個。 

a[]陣列，假設x y z為只出現一次的數，其他出現偶數次
s^=a[i] 則x^y x^z y^z 的lowbit 這三個值有一個規律，其中肯定兩個是一樣的，另外一個是不一樣的。令flips=上述三個值的異或。因此，可以利用此條件獲得某個x(或者y，或者z)，迴圈判斷的條件是 a[i]^s的lowbit==flips
解釋：a[i]^s即可劃分為兩組，一組是lowbit與flips不同，一組是lowbit與flips相同。這樣就能找到某個x,y,z，找出後，與陣列最戶一個值交換，利用find2，找出剩餘兩個。

lowbit為某個數從右往左掃描第一次出現1的位置。其實 lowbit 函式裡面寫成  mark = (x&(x-1))^x  ; return mark ; 也是可以的，功能是一樣的。

/**  ** author :hackbuteer** date   :2011-10-19   **/#include <iostream>  using namespace std;int lowbit(int x){ return x & ~(x - 1);}void Find2(int seq[], int n, int& a, int& b){ int i, xors = 0; for(i = 0; i < n; i++)  xors ^= seq[i]; int diff = lowbit(xors); a = 0,b = 0; for(i = 0; i < n; i++) {  if( diff&seq[i] )    //與運算，表示陣列中與異或結果位為1的位數相同   a ^= seq[i];  else   b ^= seq[i]; }}//三個數兩兩的異或後lowbit有兩個相同，一個不同，可以分為兩組void Find3(int seq[], int n, int& a, int& b, int& c){    int i, xors = 0;    for(i = 0; i < n; i++)        xors ^= seq[i];    int flips = 0;    for(i = 0; i < n; i++)            //因為出現偶數次的seq[i]和xors的異或，異或結果不改變        flips ^= lowbit(xors ^ seq[i]); //表示的是：flips=lowbit(a^b)^lowbit(a^c)^lowbit(b^c)    //flips = lowbit(flips);    這個是多餘的 //三個數兩兩異或後lowbit有兩個相同，一個不同，可以分為兩組 //所以flips的值為：lowbit(a^b) 或 lowbit(a^c) 或 lowbit(b^c)    //得到三個數中的一個    a = 0;    for(i = 0; i < n; i++)    {        if(lowbit(seq[i] ^ xors) == flips)     //找出三個數兩兩異或後的lowbit與另外兩個lowbit不同的那個數            a ^= seq[i];    }    //找出後，與陣列中最後一個值交換，利用Find2，找出剩餘的兩個    for(i = 0; i < n; i++)    {        if(a == seq[i])        {            int temp = seq[i];            seq[i] = seq[n - 1];            seq[n - 1] = temp;        }    }    //利用Find2，找出剩餘的兩個    Find2(seq, n - 1, b, c);}//假設陣列中只有2、3、5三個數，2與3異或後為001，2與5異或後為111，3與5異或後為110，//則flips的值為lowbit（110）= 2 ，當異或結果xors與2異或的時候，得到的就是3與5異或的結果110，其lowbit值等於flips，所以最先找出來的是三個數中的第一個數：2int main(void){ int seq[]={ 2,3,3,2,4,6,4,10,9,8,8 }; int a,b,c; Find3(seq, 11, a, b, c); cout<<a<<endl; cout<<b<<endl; cout<<c<<endl; return 0;}

8、do while(0)在巨集定義中的應用。

看linux原始碼時,經常發現有巨集定義用
#define XYZ \
do{...} while(0)
這是一個奇怪的迴圈，它根本就只會執行一次，為什麼不去掉外面的do{..}while結構呢？原來這也是非常巧妙的技巧。在工程中可能經常會引起麻煩，而上面的定義能夠保證這些麻煩不會出現。下面是解釋：

假設有這樣一個巨集定義

#define macro(condition) \

if(condition) dosomething()

現在在程式中這樣使用這個巨集：

if(temp)
    macro(i);
else
    doanotherthing();

一切看起來很正常，但是仔細想想。這個巨集會展開成：

if(temp)
    if(i) dosomething();
else
    doanotherthing();

這時的else不是與第一個if語句匹配，而是錯誤的與第二個if語句進行了匹配，編譯通過了，但是執行的結果一定是錯誤的。

為了避免這個錯誤，我們使用do{….}while(0) 把它包裹起來，成為一個獨立的語法單元，從而不會與上下文發生混淆。同時因為絕大多數的編譯器都能夠識別do{…}while(0) 這種無用的迴圈並進行優化，所以使用這種方法也不會導致程式的效能降低。

此外，這是為了含多條語句的巨集的通用性。因為預設規則是巨集定義最後是不能加分號的，分號是在引用的時候加上的。

在MFC的afx.h檔案裡面， 你會發現很多巨集定義都是用了do...while(0)或do...while(false)。

為了看起來更清晰，這裡用一個簡單點的巨集來演示：
#define SAFE_DELETE(p) do{ delete p; p = NULL } while(0)
假設這裡去掉do...while(0),
#define SAFE_DELETE(p)   delete p; p = NULL;
那麼以下程式碼：
if(NULL != p) SAFE_DELETE(p)
else   ...do sth...
就有兩個問題，
1) 因為if分支後有兩個語句，else分支沒有對應的if，編譯失敗。
2) 假設沒有else, SAFE_DELETE中的第二個語句無論if測試是否通過，會永遠執行。
你可能發現，為了避免這兩個問題，我不一定要用這個令人費解的do...while,  我直接用{}括起來就可以了
#define SAFE_DELETE(p)   { delete p; p = NULL;}
的確，這樣的話上面的問題是不存在了，但是我想對於C++程式設計師來講，在每個語句後面加分號是一種約定俗成的習慣，這樣的話，以下程式碼:
if(NULL != p)  SAFE_DELETE(p);
else   ...do sth...
由於if後面的大括號後面加了一個分號，導致其else分支就無法通過編譯了（原因同上），所以採用do...while(0)是做好的選擇了。

如果使用名家的方法

#define SAFE_FREE(p)   do {free(p);p=NULL;}  while(0)

那麼

if(NULL!=p)

        SAFE_FREE(p);

else

         do something

展開為

if(NULL!=p)

do

      { free(p);p=NULL;}

while(0);

else

        do something

好了 這樣就一切太平了。

           

給我老師的人工智慧教程打call！http://blog.csdn.net/jiangjunshow