目的

　　用勢函式的概念來確定判別函式和劃分類別介面。

基本思想

　　假設要劃分屬於兩種類別ω1和ω2的模式樣本，這些樣本可看成是分佈在n維模式空間中的點xk。 把屬於ω1的點比擬為某種能源點，在點上，電位達到峰值。 隨著與該點距離的增大，電位分佈迅速減小，即把樣本xk附近空間x點上的電位分佈，看成是一個勢函式K(x, xk)。 對於屬於ω1的樣本叢集，其附近空間會形成一個“高地”，這些樣本點所處的位置就是“山頭”。 同理，用電位的幾何分佈來看待屬於ω2的模式樣本，在其附近空間就形成“凹地”。 只要在兩類電位分佈之間選擇合適的等高線，就可以認為是模式分類的判別函式。

3.9.1 判別函式的產生

　　模式分類的判別函式可由分佈在模式空間中的許多樣本向量{xk, k=1,2,…且 }的勢函式產生。 任意一個樣本所產生的勢函式以K(x, xk)表徵，則判別函式d(x)可由勢函式序列K(x, x1)， K(x, x2)，…來構成，序列中的這些勢函式相應於在訓練過程中輸入機器的訓練模式樣本x1，x2，…。 在訓練狀態，模式樣本逐個輸入分類器，分類器就連續計算相應的勢函式，在第k步迭代時的積累位勢決定於在該步前所有的單獨勢函式的累加。 以K(x)表示積累位勢函式，若加入的訓練樣本xk+1是錯誤分類，則積累函式需要修改，若是正確分類，則不變。 

　　從勢函式可以看出，積累位勢起著判別函式的作用 當xk+1屬於ω1時，Kk(xk+1)>0；當xk+1屬於ω2時，Kk(xk+1)<0，則積累位勢不做任何修改就可用作判別函式。 由於一個模式樣本的錯誤分類可造成積累位勢在訓練時的變化，因此勢函式演算法提供了確定ω1和ω2兩類判別函式的迭代過程。 判別函式表示式 取d(x)=K(x)，則有：dk+1(x)= dk(x)+rk+1K(x, xk+1 )

3.9.2 勢函式的選擇

選擇勢函式的條件：一般來說，若兩個n維向量x和xk的函式K(x, xk)同時滿足下列三個條件，則可作為勢函式。 K(x, xk)= K(xk, x)，並且當且僅當x=xk時達到最大值； 當向量x與xk的距離趨於無窮時，K(x, xk)趨於零； K(x, xk)是光滑函式，且是x與xk之間距離的單調下降函式。

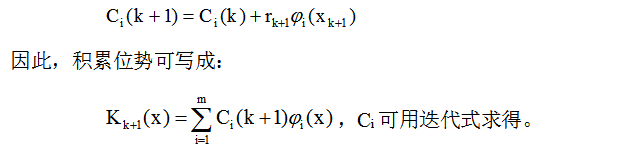
勢函式法

例項1：用第一類勢函式的演算法進行分類

（1） 選擇合適的正交函式集{}

選擇Hermite多項式，其正交域為(-∞, +∞)，其一維形式是

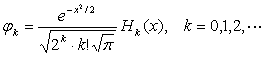
其正交性：

其中，H_k(x)前面的乘式為正交歸一化因子，為計算簡便可省略。因此，Hermite多項式前面幾項的表示式為

H₀(x)=1, H₁(x)=2x, H₂(x)=4x²-2,

H₃(x)=8x³-12x, H₄(x)=16x⁴-48x²+12

（2） 建立二維的正交函式集

二維的正交函式集可由任意一對一維的正交函式組成，這裡取四項最低階的二維的正交函式

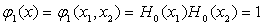
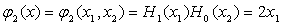
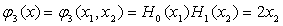
（3） 生成勢函式

按第一類勢函式定義，得到勢函式

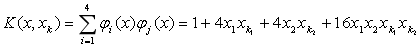
其中，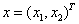

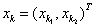
（4） 通過訓練樣本逐步計算累積位勢K(x)

給定訓練樣本：ω₁類為x_①=(1 0)^T, x_②=(0 -1)^T

ω₂類為x_③=(-1 0)^T, x_④=(0 1)^T

累積位勢K(x)的迭代演算法如下

第一步：取x_①=(1 0)^T∈ω₁，故

K₁(x)=K(x, x_①)=1+4x₁·1+4x₂·0+16x₁x₂·1·0=1+4x₁

第二步：取x_②=(0 -1)^T∈ω₁，故K₁(x_②)=1+4·0=1

因K₁(x_②)>0且x_②∈ω₁，故K₂(x)=K₁(x)=1+4x₁

第三步：取x_③=(-1 0)^T∈ω₂，故K₂(x_③)=1+4·(-1)=-3

因K₂(x_③)<0且x_③∈ω₂，故K₃(x)=K₂(x)=1+4x₁

第四步：取x_④=(0 1)^T∈ω₂，故K₃(x_④)=1+4·0=1

因K₃(x_④)>0且x_④∈ω₂，

故K₄(x)=K₃(x)-K(x,x_④)=1+4x₁-(1+4x₂)=4x₁-4x₂

將全部訓練樣本重複迭代一次，得

第五步：取x_⑤=x_①=(1 0)^T∈ω₁，K₄(x_⑤)=4

故K₅(x)=K₄(x)=4x₁-4x₂

第六步：取x_⑥=x_②=(0 -1)^T∈ω₁，K₅(x_⑥)=4

故K₆(x)=K₅(x)=4x₁-4x₂

第七步：取x_⑦=x_③=(-1 0)^T∈ω₂，K₆(x_⑦)=-4

故K₇(x)=K₆(x)=4x₁-4x₂

第八步：取x_⑧=x_④=(0 1)^T∈ω₂，K₇(x_⑧)=-4

故K₈(x)=K₇(x)=4x₁-4x₂

以上對全部訓練樣本都能正確分類，因此演算法收斂於判別函式

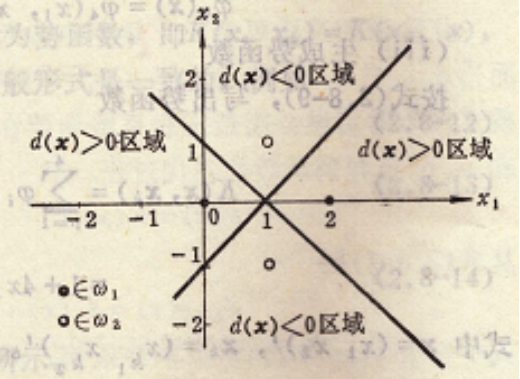
d(x)=4x₁-4x₂

例項2：用第二類勢函式的演算法進行分類

選擇指數型勢函式，取α=1，在二維情況下勢函式為

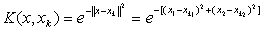
這裡：ω₁類為x_①=(0 0)^T, x_②=(2 0)^T

ω₂類為x_③=(1 1)^T, x_④=(1 -1)^T

可以看出，這兩類模式是線性不可分的。演算法步驟如下：

第一步：取x_①=(0 0)^T∈ω₁，則

K₁(x)=K(x,x_①)=

第二步：取x_②=(2 0)^T∈ω₁

因K₁(x_②)=e^-(4+0)=e^-4>0，

故K₂(x)=K₁(x)=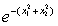

第三步：取x_③=(1 1)^T∈ω₂

因K₂(x_③)=e^-(1+1)=e^-2>0，

故K₃(x)=K₂(x)-K(x,x_③)=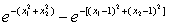

第四步：取x_④=(1 -1)^T∈ω₂

因K₃(x_④) =e^-(1+1)-e^-(0+4)=e^-2-e^-4>0，

故K₄(x)=K₃(x)-K(x,x_④)

=

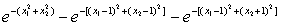
需對全部訓練樣本重複迭代一次

第五步：取x_⑤=x_①=(0 0)^T∈ω₁，K₄(x_⑤)=e⁰-e^-2-e^-2=1-2e^-2>0

故K₅(x)=K₄(x)

第六步：取x_⑥=x_②=(2 0)^T∈ω₁，K₅(x_⑥)=e^-4-e^-2-e^-2=e^-4-2e^-2<0

故K₆(x)=K₅(x)+K(x,x_⑥)

=

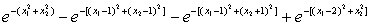
第七步：取x_⑦=x_③=(1 1)^T∈ω₂，K₆(x_⑦)=e^-2-e⁰-e^-4+e^-2=2e^-2-e^-4-1<0

故K₇(x)=K₆(x)

第八步：取x_⑧=x_④=(1 -1)^T∈ω₂，K₇(x_⑧)=e^-2-e^-4-e⁰+e^-2=2e^-2-e^-4-1<0

故K₈(x)=K₇(x)

第九步：取x_⑨=x_①=(0 0)^T∈ω₁，K₈(x_⑨)=e⁰-e^-2-e^-2+e^-4=1+e^-4-2e^-2>0

故K₉(x)=K₈(x)

第十步：取x_⑩=x_②=(2 0)^T∈ω₁，K₉(x_⑩)=e^-4-e^-2-e^-2+e⁰=1+e^-4-2e^-2>0

故K₁₀(x)=K₉(x)

經過上述迭代，全部模式都已正確分類，因此演算法收斂於判別函式

討論

用第二類勢函式，當訓練樣本維數和數目都較高時，需要計算和儲存的指數項較多。 正因為勢函式由許多新項組成，因此有很強的分類能力。