關於似然函式和最大似然估計的詳細說明可以看這篇文章：https://blog.csdn.net/zgcr654321/article/details/83382729

二分類情況和多分類情況下的似然函式與最大似然估計：

二分類情況下的似然函式與最大似然估計：

我們知道按照生活中的常識，一個均勻的硬幣丟擲落在地上，它是正面或者反面的概率是0.5。但是，有很多事物發生的概率我們並不能這樣直觀的估計到。

如：

假設一個袋子裝有白球與紅球，但比例未知，現在抽取10次（每次抽完都放回，保證事件獨立性），現在我們抽取10次，抽到了7次白球和3次紅球。

我們先設是白球的概率為x，則是紅球的概率為1-x。

我們抽取10次，抽到了7次白球和3次紅球。

根據這10次的結果，我們就可以列出其似然函式：

又似然函式的L(x)值越大，則表明此時對應的x值“可能性越大”，即此時的x值最有可能接近真實分佈中的x值（x是一個概率）。

那麼在概率論和數理統計中如何求這個x值呢？

我們先把L(x)寫成lnL(x)的形式，由於lnL(x)與L(x)相同的極大值點，且對數函式更好求導，所以我們只要對lnL(x)求導，令導數為0反求對應x的值，x就是一個可能的極大值點，事實上，這個點往往只有一個。

對數似然函式：

對lnL(x)求導：

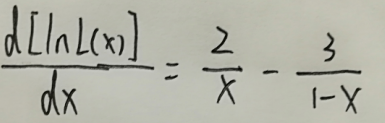
接下來我們令導數為0，得到下式即為對數似然方程：

解這個方程，可得x=0.4。

這個x值就是我們利用這5次拋硬幣的結果推測出的最有可能接近拋硬幣得到正面的真實概率的概率。

多分類情況下的似然函式與最大似然估計：

假設我們有一個六面體的骰子，骰子扔出後必定有某一個面朝下，而哪個面朝下的概率我們並不知道。

現在我們將骰子扔出15次，其中面1朝下2次，面2朝下3次，面3朝下4次，面4朝下1次，面5朝下2次，面6朝下3次。

我們分別設面1-面6朝下的概率分別為x1、x2、x3、x4、x5、x6。

根據這15次的結果，我們可以列出似然函式：

其對數似然函式：

由於這裡的似然函式有多個獨立的自變數，所以是對數似然方程組：

當然，這個方程組我們解不出來。

實際上，在概率論與數理統計中，往往多個自變數之間有相互的聯絡。這使得似然函式最終可以化為只有一個自變數的函式。

例如：

已知X是離散型隨機變數，可能的取值有0，1,  2。對應概率為：

我們對X抽取容量為10的樣本，其中有2個0、5個1、3個2，求θ的最大似然估計值。

似然函式：

對數似然函式：

對對數似然函式求導，並令導數為0，解θ：

得到θ的最大似然估計值為9/20。

那麼二分類的似然函式和多分類的似然函式與機器學習中的交叉熵函式又有什麼關係呢？

機器學習中的交叉熵函式：

什麼是資訊量？

假設X是一個離散型隨機變數，其取值集合為X，概率分佈函式為p(x)=Pr(X=x),x∈X，我們定義事件X=x0的資訊量為： 

可以理解為，一個事件發生的概率越大，則它所攜帶的資訊量就越小，而當p(x0)=1時，熵將等於0，也就是說該事件的發生不會導致任何資訊量的增加。

舉例：

小明平時不愛學習，考試經常不及格，而小王是個勤奮學習的好學生，經常得滿分，所以我們可以做如下假設： 

事件A：小明考試及格，對應的概率P(xA)=0.1，資訊量為I(xA)=−log(0.1)=3.3219
事件B：小王考試及格，對應的概率P(xB)=0.999，資訊量為I(xB)=−log(0.999)=0.0014

可以看出，結果非常符合直觀：

小明及格的可能性很低(十次考試只有一次及格)，因此如果某次考試及格了（大家都會說：XXX竟然及格了！），必然會引入較大的資訊量，對應的I值也較高。而對於小王而言，考試及格是大概率事件，在事件B發生前，大家普遍認為事件B的發生幾乎是確定的，因此當某次考試小王及格這個事件發生時並不會引入太多的資訊量，相應的I值也非常的低。

什麼是熵？

還是通過上邊的例子來說明，假設小明的考試結果是一個0-1分佈XA，只有兩個取值{0：不及格，1：及格}。

在某次考試結果公佈前，小明的考試結果有多大的不確定度呢？你肯定會說：十有八九不及格！因為根據先驗知識，小明及格的概率僅有0.1,90%的可能都是不及格的。怎麼來度量這個不確定度？求期望！不錯，我們對所有可能結果帶來的額外資訊量求取均值（期望），其結果不就能夠衡量出小明考試成績的不確定度了嗎。 

即： 
HA(x)=−[p(xA)log(p(xA))+(1−p(xA))log(1−p(xA))]=0.4690

對應小王的熵： 
HB(x)=−[p(xB)log(p(xB))+(1−p(xB))log(1−p(xB))]=0.0114

雖然小明考試結果的不確定性較低，畢竟十次有9次都不及格，但是也比不上小王（1000次考試只有一次才可能不及格，結果相當的確定） 

我們再假設一個成績相對普通的學生小東，他及格的概率是P(xC)=0.5，即及格與否的概率是一樣的，對應的熵： 
HC(x)=−[p(xC)log(p(xC))+(1−p(xC))log(1−p(xC))]=1

其熵為1，他的不確定性比前邊兩位同學要高很多，在成績公佈之前，很難準確猜測出他的考試結果。 

從上面可以看出，熵其實是資訊量的期望值，它是一個隨機變數的確定性的度量。熵越大，變數的取值越不確定，反之就越確定。

對於一個隨機變數X而言，它的所有可能取值的資訊量的期望（E[I(x)]）就稱為熵。 

X的熵定義為： 

如果p(x)是連續型隨機變數的pdf，則熵定義為： 

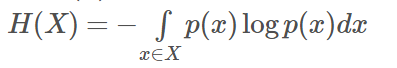
為了保證有效性，這裡約定當p(x)→0時,有p(x)logp(x)→0

當X為0-1分佈時，熵與概率p的關係如下圖： 

 
可以看出，當兩種取值的可能性相等時，不確定度最大（此時沒有任何先驗知識），這個結論可以推廣到多種取值的情況。

在圖中也可以看出，當p=0或1時，熵為0，即此時X完全確定。 

熵的單位隨著公式中log運算的底數而變化，當底數為2時，單位為“位元”(bit)，底數為e時，單位為“奈特”。

什麼是相對熵？

相對熵(relative entropy)又稱為KL散度（Kullback-Leibler divergence），KL距離，是兩個隨機分佈間距離的度量。記為。它度量當真實分佈為p時，假設分佈q的無效性。 

為了保證連續性，做如下約定： 

顯然，當p=q時,兩者之間的相對熵

表示在p分佈下，使用q進行編碼需要的bit數，而H(p)表示對真實分佈p所需要的最小編碼bit數。

故相對熵的含義為：

表示在真實分佈為p的前提下，使用q分佈進行編碼相對於使用真實分佈p進行編碼（即最優編碼）所多出來的bit數。

什麼是交叉熵？

交叉熵容易跟相對熵搞混，二者聯絡緊密，但又有所區別。

假設有兩個分佈p，q，則它們在給定樣本集上的交叉熵定義如下： 

可以看出，交叉熵與上一節定義的相對熵僅相差了H(p)。

當p已知時，可以把H(p)看做一個常數，此時交叉熵與KL距離在行為上是等價的，都反映了分佈p，q的相似程度。最小化交叉熵等於最小化KL距離。它們都將在p=q時取得最小值H(p)（p=q時KL距離為0），因此有的工程文獻中將最小化KL距離的方法稱為Principle of Minimum Cross-Entropy (MCE)或Minxent方法。 

特別的，在logistic regression中：

p:真實樣本分佈，服從引數為p的0-1分佈，即X∼B(1,p)X∼B(1,p) 
q:待估計的模型，服從引數為q的0-1分佈，即X∼B(1,q)X∼B(1,q) 

兩者的交叉熵為： 

對所有訓練樣本取均值得： 

這個結果與通過最大似然估計方法求出來的結果一致。

在機器學習中的交叉熵函式寫法：

二分類問題的loss函式（輸入資料是softmax或sigmoid函式的輸出）：

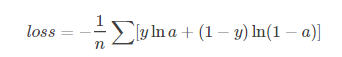
多分類問題使用的loss函式（輸入資料是softmax或sigmoid函式的輸出）：

如果是在tensorflow中，loss函式往往寫成下面這兩種形式之一：

loss = tf.reduce_mean(- tf.reduce_sum(y * tf.log(pred), 1))

loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=output, labels=Y))

看到上面的二分類和多分類問題使用的loss函式，再跟似然函式比對一下，是不是覺得有點像呢？

事實上，loss函式和對數似然函式形式完全一樣。

如果我們從最大似然估計的角度來解讀loss函式，那麼是這樣的：

假如我們的資料集是mnist，這是一個0-9的手寫體數字的資料集，如果我們從其中抽出一個圖片，總共只有10種可能，即數字0-9。

一般情況下我們每一次訓練都是取一個批樣本（batch_size）。

我們現在假設batch_size為1，即每次訓練只取一個樣本。

我們將這個批樣本輸入神經網路中進行計算，最後得到經過softmax函式或sigmoid函式處理後的輸出資料，這個輸出資料是我們預測的這batchsize個圖片的標籤向量，它代表了我們的神經網路預測的這輸入的batchsize個樣本的每個圖片分別是哪一類圖片（具體到mnist資料集裡，就是圖片是數字0-9中的哪一個）。

預測的標籤向量的形式為：

[a0,a1,a2,a3,a4,a5,a6,a7,a8,a9]

我們的真實標籤也是一個有著同樣元素數量的向量，一般寫作：

[y0,y1,y2,y3,y4,y5,y6,y7,y8,y9]

且真實標籤中除了代表自己是哪個數字的那個下標的元素是1，其他都是0，如[0,0,0,0,0,1,0,0,0,0]代表數字5。

如果我們把一個圖片屬於數字0-9中的一個看成10個獨立事件，其實這個標籤向量代表的就是10個獨立事件的概率。

而真實標籤代表的就是我們抽取的一個樣本。這一個樣本中必然會發生一個事件，而其他9個事件都不發生。

現在再看看多分類的loss函式：

還記得上面的多分類的似然函式的形式嗎？就是這個：

現在回到我們的mnist識別問題，對於loss函式，我們的樣本只有1個了，我們現在抽了一個樣本是數字7。

設圖片是數字0-9的概率分別是x0，x1，x2，x3，x4，x5，x6，x7，x8，x9，那麼似然函式為：

對數似然函式為：

這個形式是不是與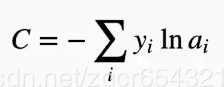一樣呢？很顯然是一樣的。

為什麼多了一個負號？

因為ai總是在0到1之間，而yi值不是0就是1，這就導致每一項要麼為0，要麼是負數。而tensorflow的優化器是向著loss值降低的方向優化的，並且最終目標是loss值儘可能接近0，所以要求loss函式是一個大於0的值。因此我們加一個負號。

同上面的多分類最大似然估計問題一樣，我們一般情況下很難求極值點。

在機器學習中，通過tensorflow使用梯度下降或其他的優化方法，我們可以不斷地更新權重引數，最終使得loss函式從一個正值減小到接近0（也就是似然函式從原來的負值逐漸接近0,在這個mnist的例子中顯然0是似然函式的極大值）求出一個接近似然函式極大值的點，這就是我們求出的一個接近極大似然估計值的一組ai值。

也就是說，loss函式值越小，求得的ai值代表的概率越有可能是真實概率。

二分類的loss函式也與上面的原理類似，事實上，二分類的loss函式可以用多分類的loss函式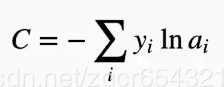

來表達，它們的結果完全一樣。

在李航的《統計學習方法》一書中的6.1.3中，推導了二分類的對數似然函式，如下：

如果有興趣，可以自己詳細看看書上的推導過程。

假如batch_size為100（或大於1的其他數），我們的loss函式又是如何處理的呢？

其實看我們在tensorflow中的loss函式變數的定義就知道了：

loss = tf.reduce_mean(- tf.reduce_sum(y * tf.log(pred), 1))

這個loss函式的意思是，yi與對應的ln(ai)相乘後，使用tf.reduce_sum函式將相乘後的這個向量（相乘後的向量形式是shape=(batch_size、10)的張量）按行求和（其實就是求出了每一個樣本的loss值）,然後按列求和後求平均值。

也就是說，當輸入一個批樣本時，我們使用tensorflow優化器更新權重的依據是這一批樣本的loss值的平均值。然後通過求loss對各個權重的梯度（鏈式求導法則），再用梯度更新各個權重。

舉例：

假設有一個三分類問題。

第一個樣例的正確答案是(1, 0, 0)，經過softmax後的預測答案是(0.5, 0.4, 0.1)

則它和正確答案的交叉熵為： H( (1,0,0) , (0.5,0.4,0.1) ) = - ( 1*log0.5 + 0*log0.4 + 0*log0.1 ) ≈ 0.3

另一個樣例經過softmax的預測值是(0.8, 0.1, 0.1)

則他和正確答案的交叉熵是 ： H( (1, 0, 0), (0.8, 0.1, 0.1) ) = - ( 1*log0.8 + 0*log0.1 + 0*log0.1 ) ≈ 0.1

 

從直觀上看容易知道第二個優於第一個，通過交叉熵計算結果也是一致的。所以我們的優化器總是向著loss值減小的方向去優化。