轉載自：https://blog.dynox.cn/?p=1562

AES簡介

AES, Advanced Encryption Standard，其實是一套標準：FIPS 197，而我們所說的AES演算法其實是Rijndael演算法。

NIST (National INstitute of Standards and Technology) 在1997年9月12日公開徵集更高效更安全的替代DES加密演算法，第一輪共有15種演算法入選，其中5種演算法入圍了決賽，分別是MARS，RC6，Rijndael，Serpent和Twofish。又經過3年的驗證、評測及公眾討論之後Rijndael演算法最終入選。

Rijndael演算法

Rijndael演算法是由比利時學者Joan Daemen和Vincent Rijmen所提出的，演算法的名字就由兩位作者的名字組合而成。Rijndael的優勢在於集安全性、效能、效率、可實現性及靈活性與一體。

Joan Daemen和Vincent Rijmen

AES vs Rijndael

Rijndael演算法支援多種分組及金鑰長度，介於128-256之間所有32的倍數均可，最小支援128位，最大256位，共25種組合。而AES標準支援的分組大小固定為128位，金鑰長度有3種選擇：128位、192位及256位。

加密例項

下面針對16位元組的簡單明文字串“0011223344....eeff”，分別用AES-128/AES-192及AES-256進行加密運算：

AES-128

金鑰選用16位元組長的簡單字串：“00010203....0e0f” 來，上面的明文經過加密變換後成為"69c4e0d8....6089"。

plain :  00 11 22 33 44 55 66 77 88 99 aa bb cc dd ee ff
key   :  00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f
cypher:  69 c4 e0 d8 6a 7b 04 30 d8 cd b7 80 70 b4 c5 5a

AES-192

plain :  00 11 22 33 44 55 66 77 88 99 aa bb cc dd ee ff
key   :  00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d .. .. .. 17
cypher:  dd a9 7c a4 86 4c df e0 6e af 70 a0 ec 0d 71 91
 

AES-256

plain :  00 11 22 33 44 55 66 77 88 99 aa bb cc dd ee ff
key   :  00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d .. .. .. 17 .. .. .. 1f
cypher:  8e a2 b7 ca 51 67 45 bf ea fc 49 90 4b 49 60 89

總體結構

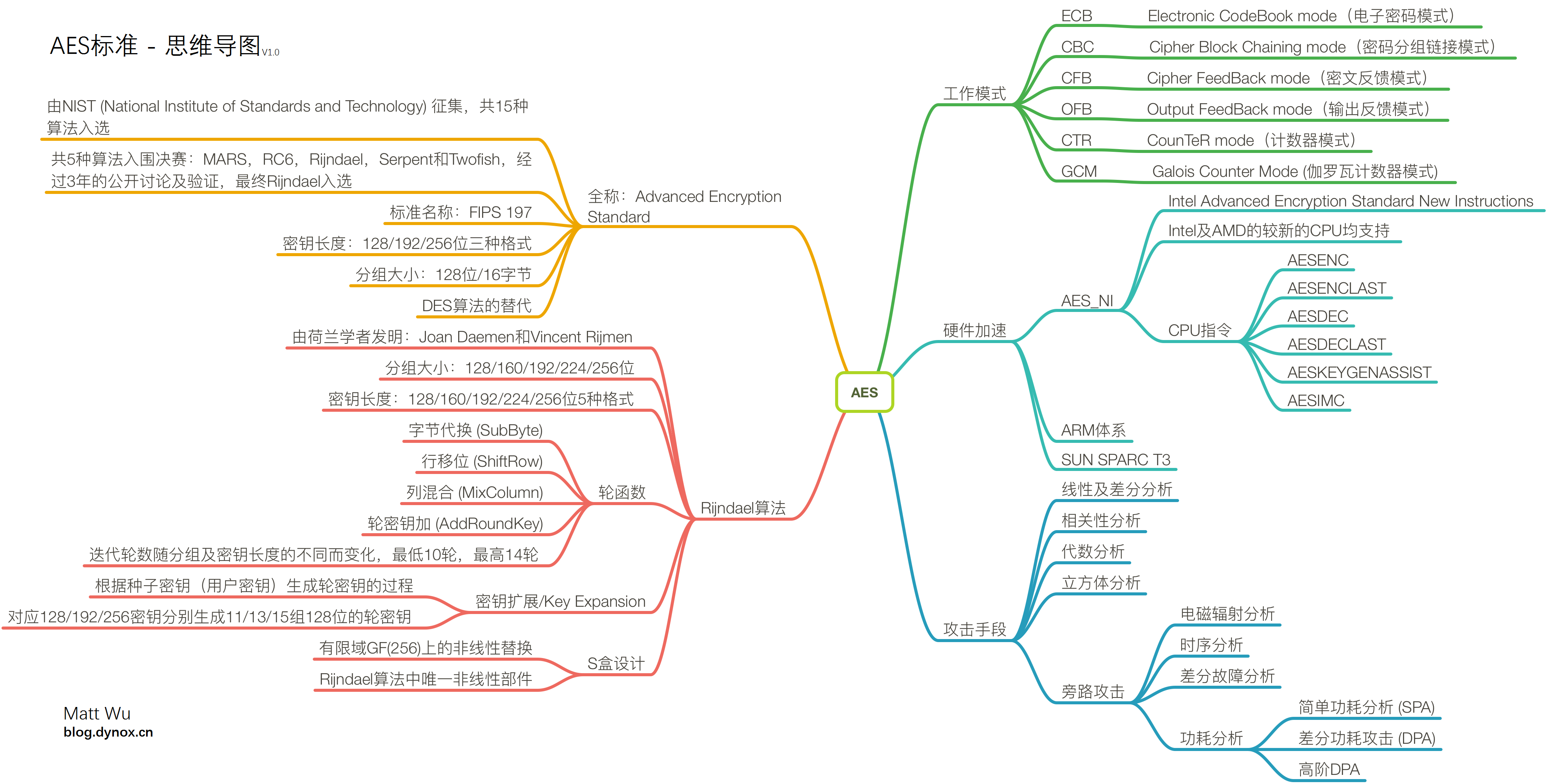
Rijndael演算法是基於代換-置換網路（SPN，Substitution-permutation network）的迭代演算法。明文資料經過多輪次的轉換後方能生成密文，每個輪次的轉換操作由輪函式定義。輪函式任務就是根據金鑰編排序列（即輪密碼）對資料進行不同的代換及置換等操作。

圖左側為輪函式的流程，主要包含4種主要運算操作：位元組代換(SubByte)、行移位(ShiftRow)、列混合(MixColumn)、輪金鑰加(AddRoundKey)。圖右側為金鑰編排方案，在Rijndael中稱為金鑰擴充套件演算法（KeyExpansion）。

AES標準演算法將128位的明文，以特定次序生成一個4x4的矩陣（每個元素是一個位元組，8位），即初始狀態（state），經由輪函式的迭代轉換之後又將作為下一輪迭代的輸入繼續參與運算直到迭代結束。

Rijndael演算法支援大於128位的明文分組，所以需要列數更多的矩陣來描述。Rijndael輪函式的運算是在特殊定義的有限域GF(256)上進行的。有限域（Finite Field）又名伽羅瓦域（Galois field），簡單言之就是一個滿足特定規則的集合，集合中的元素可以進行加減乘除運算，且運算結果也是屬於此集合。更詳細有有關Rijndael演算法的數學描述，可以參閱本文最後所羅列的參考資料，在此不做熬述。

輪函式

我們已經得知輪函式主要包含4種運算，但不同的運算輪所做的具體運的算組合並不相同。主要區別是初始輪（Round: 0）和最後一輪（Round: Nr），所有中間輪的運算都是相同的，會依次進行4種運算，即：

1. 位元組代換(SubByte)
2. 行移位(ShiftRow)
3. 列混合(MixColumn)
4. 輪金鑰加(AddRoundKey)

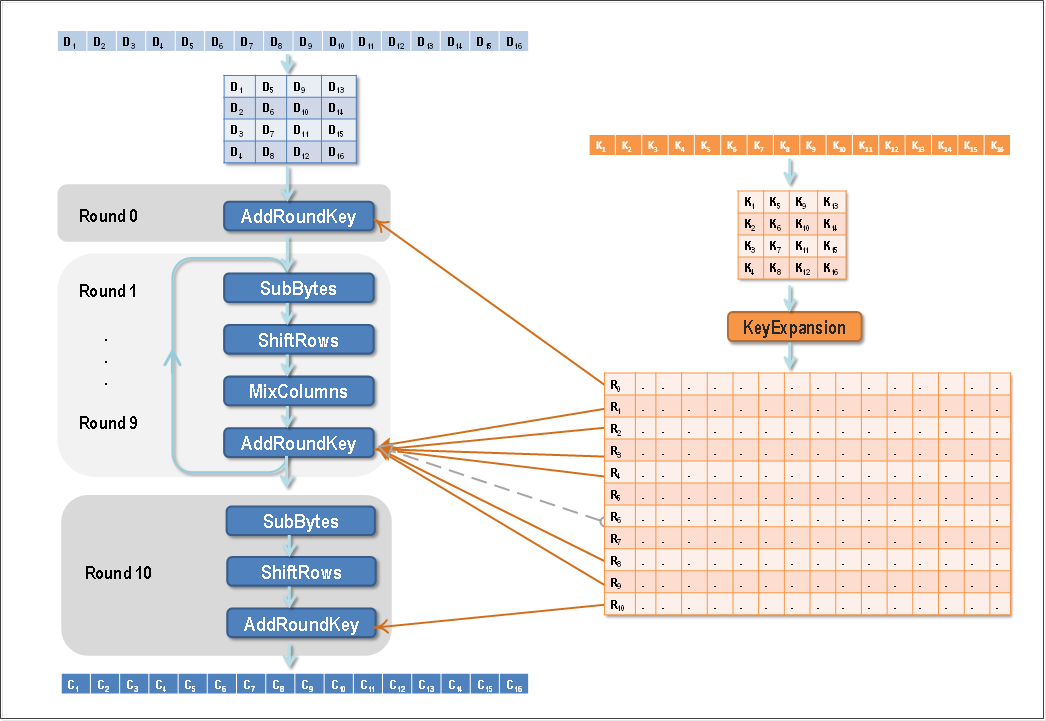
根據Rinjdael演算法的定義，加密輪數會針對不同的分組及不同的金鑰長度選擇不同的數值：

AES標準只支援128位分組（Nb = 4）的情況。

輪函式的實現程式碼如下，直接實現在加密函式內部迴圈中：

int aes_encrypt(AES_CYPHER_T mode, uint8_t *data, int len, uint8_t *key)
{
    uint8_t w[4 * 4 * 15] = {0}; /* round key */
    uint8_t s[4 * 4] = {0}; /* state */

    int nr, i, j;

    /* key expansion */
    aes_key_expansion(mode, key, w);

    /* start data cypher loop over input buffer */
    for (i = 0; i < len; i += 4 * g_aes_nb[mode]) {

        /* init state from user buffer (plaintext) */
        for (j = 0; j < 4 * g_aes_nb[mode]; j++)
            s[j] = data[i + j];

        /* start AES cypher loop over all AES rounds */
        for (nr = 0; nr <= g_aes_rounds[mode]; nr++) {

            if (nr > 0) {

                /* do SubBytes */
                aes_sub_bytes(mode, s);

                /* do ShiftRows */
                aes_shift_rows(mode, s);

                if (nr < g_aes_rounds[mode]) {
                    /* do MixColumns */
                    aes_mix_columns(mode, s);
                }
            }

            /* do AddRoundKey */
            aes_add_round_key(mode, s, w, nr);
        }

        /* save state (cypher) to user buffer */
        for (j = 0; j < 4 * g_aes_nb[mode]; j++)
            data[i + j] = s[j];
    }

    return 0;
}

動畫演示加密過程

Enrique Zabala建立了一個AES-128加密演算法的動畫演示，清楚、直觀地介紹了輪函式執行的過程。點選可直接觀看。

輪函式拆解：位元組代換（Substitute Bytes）

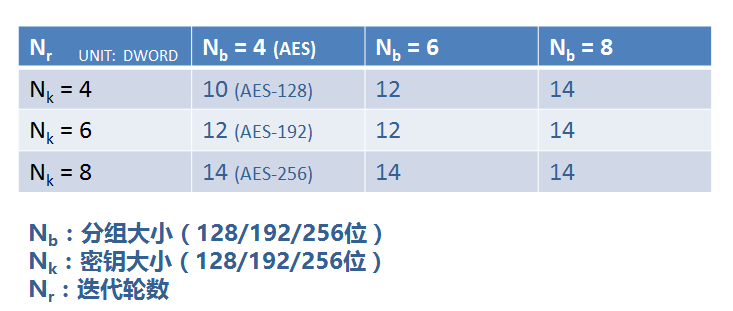
位元組代換（SubBytes）是對state矩陣中的每一個獨立元素於置換盒 （Substitution-box，S盒）中進行查詢並以此替換輸入狀態的操作。位元組代換是可逆的非線性變換，也是AES運算組中唯一的非線性變換。位元組代換逆操作也是通過逆向置換盒的查詢及替換來完成的。

S盒是事先設計好的16x16的查詢表，即256個元素。其設計不是隨意的，要根據設計原則嚴格計算求得，不然無法保證演算法的安全性。既然是S盒是計算得來，所以位元組代換的操作完全可以通過計算來完成，不過通過S盒查表操作更方便快捷，圖中所示就是通過S盒查詢對應元素進行的替換操作。

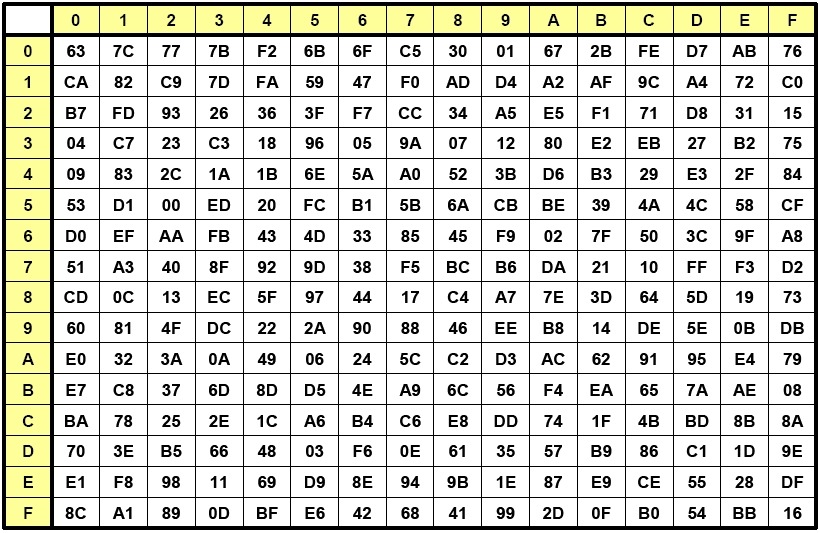
void aes_sub_bytes(AES_CYPHER_T mode, uint8_t *state)
{
    int i, j;

    for (i = 0; i < g_aes_nb[mode]; i++) {
        for (j = 0; j < 4; j++) {
            state[i * 4 + j] = aes_sub_sbox(state[i * 4 + j]);
        }
    }
}

例項說明：

   input:  00 10 20 30 40 50 60 70 80 90 a0 b0 c0 d0 e0 f0
     sub:  63 ca b7 04 09 53 d0 51 cd 60 e0 e7 ba 70 e1 8c

輪函式拆解：行移位（Shift Rows）

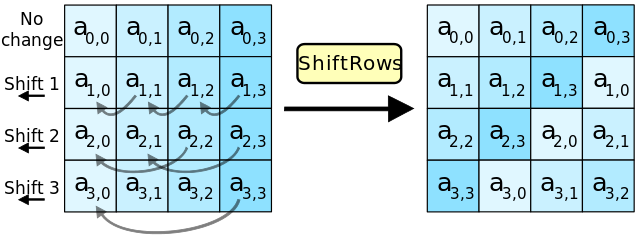
行移位主要目的是實現位元組在每一行的擴散，屬於線性變換。

void aes_shift_rows(AES_CYPHER_T mode, uint8_t *state)
{
    uint8_t *s = (uint8_t *)state;
    int i, j, r;

    for (i = 1; i < g_aes_nb[mode]; i++) {
        for (j = 0; j < i; j++) {
            uint8_t tmp = s[i];
            for (r = 0; r < g_aes_nb[mode]; r++) {
                s[i + r * 4] = s[i + (r + 1) * 4];
            }
            s[i + (g_aes_nb[mode] - 1) * 4] = tmp;
        }
    }
}

例項說明：

     sub:  63 ca b7 04 09 53 d0 51 cd 60 e0 e7 ba 70 e1 8c
   shift:  63 53 e0 8c 09 60 e1 04 cd 70 b7 51 ba ca d0 e7

輪函式拆解：列混合（Mix Columns）

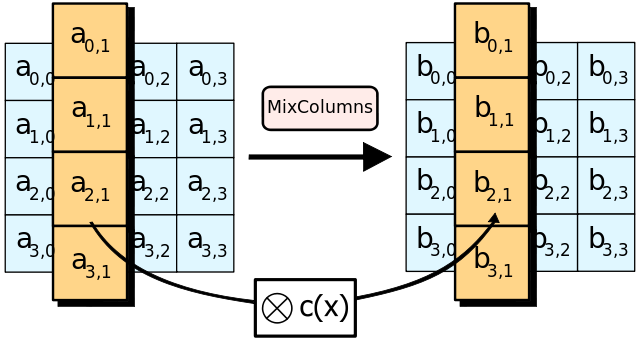
列混合是通過將state矩陣與常矩陣C相乘以達成在列上的擴散，屬於代替變換。列混合是Rijndael演算法中最複雜的一步，其實質是在有限域GF(256)上的多項式乘法運算。

void aes_mix_columns(AES_CYPHER_T mode, uint8_t *state)
{
    uint8_t y[16] = { 2, 3, 1, 1,  1, 2, 3, 1,  1, 1, 2, 3,  3, 1, 1, 2};
    uint8_t s[4];
    int i, j, r;

    for (i = 0; i < g_aes_nb[mode]; i++) {
        for (r = 0; r < 4; r++) {
            s[r] = 0;
            for (j = 0; j < 4; j++) {
                s[r] = s[r] ^ aes_mul(state[i * 4 + j], y[r * 4 + j]);
            }
        }
        for (r = 0; r < 4; r++) {
            state[i * 4 + r] = s[r];
        }
    }
}

例項說明：

   shift:  63 53 e0 8c 09 60 e1 04 cd 70 b7 51 ba ca d0 e7
     mix:  5f 72 64 15 57 f5 bc 92 f7 be 3b 29 1d b9 f9 1a

輪函式拆解：輪金鑰加（Add Round Key）

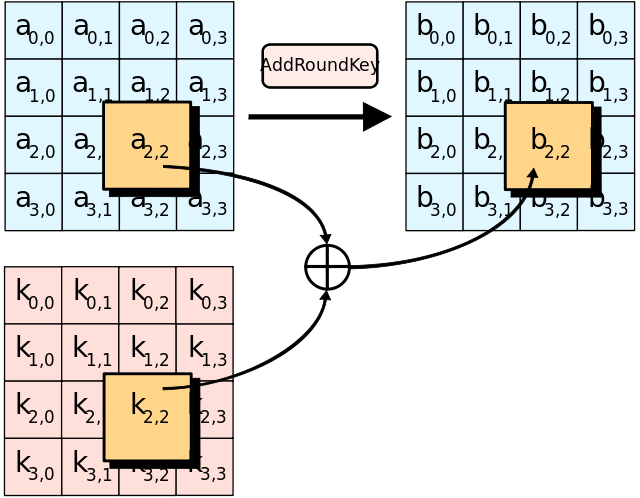
金鑰加是將輪金鑰簡單地與狀態進行逐位元異或。實現程式碼如下：

void aes_add_round_key(AES_CYPHER_T mode, uint8_t *state,
                       uint8_t *round, int nr)
{
    uint32_t *w = (uint32_t *)round;
    uint32_t *s = (uint32_t *)state;
    int i;

    for (i = 0; i < g_aes_nb[mode]; i++) {
        s[i] ^= w[nr * g_aes_nb[mode] + i];
    }
}

例項說明：

     mix:  5f 72 64 15 57 f5 bc 92 f7 be 3b 29 1d b9 f9 1a
   round:  d6 aa 74 fd d2 af 72 fa da a6 78 f1 d6 ab 76 fe
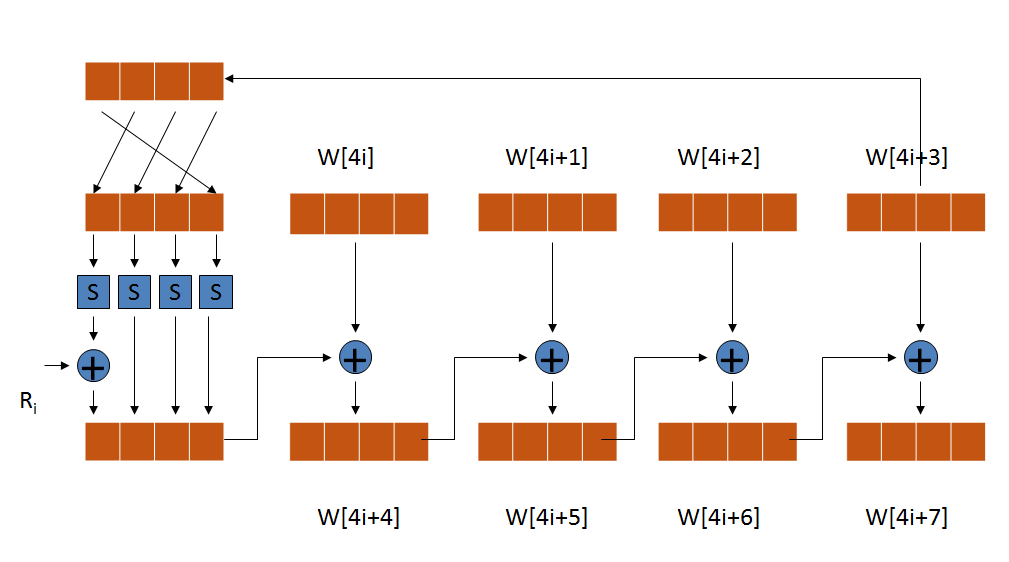
   state:  89 d8 10 e8 85 5a ce 68 2d 18 43 d8 cb 12 8f e4

金鑰擴充套件演算法（Key Expansion）

金鑰擴充套件演算法是Rijndael的金鑰編排實現演算法，其目的是根據種子金鑰（使用者金鑰）生成多組輪金鑰。輪金鑰為多組128位金鑰，對應不同金鑰長度，分別是11，13，15組。

實現程式碼：

/*
 * nr: number of rounds
 * nb: number of columns comprising the state, nb = 4 dwords (16 bytes)
 * nk: number of 32-bit words comprising cipher key, nk = 4, 6, 8 (KeyLength/(4*8))
 */

void aes_key_expansion(AES_CYPHER_T mode, uint8_t *key, uint8_t *round)
{
    uint32_t *w = (uint32_t *)round;
    uint32_t  t;
    int      i = 0;

    do {
        w[i] = *((uint32_t *)&key[i * 4 + 0]);
    } while (++i < g_aes_nk[mode]);

    do {
        if ((i % g_aes_nk[mode]) == 0) {
            t = aes_rot_dword(w[i - 1]);
            t = aes_sub_dword(t);
            t = t ^ aes_swap_dword(g_aes_rcon[i/g_aes_nk[mode] - 1]);
        } else if (g_aes_nk[mode] > 6 && (i % g_aes_nk[mode]) == 4) {
            t = aes_sub_dword(w[i - 1]);
        } else {
            t = w[i - 1];
        }
        w[i] = w[i - g_aes_nk[mode]] ^ t;

    } while (++i < g_aes_nb[mode] * (g_aes_rounds[mode] + 1));

    /* key can be discarded (or zeroed) from memory */
}

以AES-128為例，從128位種子金鑰生成11組輪金鑰（每組128位）：

Input:
    key :  00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f
Key Expansion:
    00:  rs: 00010203
    01:  rs: 04050607
    02:  rs: 08090a0b
    03:  rs: 0c0d0e0f
    04:  rot: 0d0e0f0c sub: d7ab76fe rcon: 01000000 xor: fe76abd6 rs: d6aa74fd
    05:  equ: d6aa74fd rs: d2af72fa
    06:  equ: d2af72fa rs: daa678f1
    07:  equ: daa678f1 rs: d6ab76fe
    08:  rot: ab76fed6 sub: 6238bbf6 rcon: 02000000 xor: f6bb3860 rs: b692cf0b
    09:  equ: b692cf0b rs: 643dbdf1
    10:  equ: 643dbdf1 rs: be9bc500
    11:  equ: be9bc500 rs: 6830b3fe
    12:  rot: 30b3fe68 sub: 046dbb45 rcon: 04000000 xor: 45bb6d00 rs: b6ff744e
    13:  equ: b6ff744e rs: d2c2c9bf
    14:  equ: d2c2c9bf rs: 6c590cbf
    15:  equ: 6c590cbf rs: 0469bf41
    16:  rot: 69bf4104 sub: f90883f2 rcon: 08000000 xor: f28308f1 rs: 47f7f7bc
    17:  equ: 47f7f7bc rs: 95353e03
    18:  equ: 95353e03 rs: f96c32bc
    19:  equ: f96c32bc rs: fd058dfd
    20:  rot: 058dfdfd sub: 6b5d5454 rcon: 10000000 xor: 54545d7b rs: 3caaa3e8
    21:  equ: 3caaa3e8 rs: a99f9deb
    22:  equ: a99f9deb rs: 50f3af57
    23:  equ: 50f3af57 rs: adf622aa
    24:  rot: f622aaad sub: 4293ac95 rcon: 20000000 xor: 95ac9362 rs: 5e390f7d
    25:  equ: 5e390f7d rs: f7a69296
    26:  equ: f7a69296 rs: a7553dc1
    27:  equ: a7553dc1 rs: 0aa31f6b
    28:  rot: a31f6b0a sub: 0ac07f67 rcon: 40000000 xor: 677fc04a rs: 14f9701a
    29:  equ: 14f9701a rs: e35fe28c
    30:  equ: e35fe28c rs: 440adf4d
    31:  equ: 440adf4d rs: 4ea9c026
    32:  rot: a9c0264e sub: d3baf72f rcon: 80000000 xor: 2ff7ba53 rs: 47438735
    33:  equ: 47438735 rs: a41c65b9
    34:  equ: a41c65b9 rs: e016baf4
    35:  equ: e016baf4 rs: aebf7ad2
    36:  rot: bf7ad2ae sub: 08dab5e4 rcon: 1b000000 xor: e4b5da13 rs: 549932d1
    37:  equ: 549932d1 rs: f0855768
    38:  equ: f0855768 rs: 1093ed9c
    39:  equ: 1093ed9c rs: be2c974e
    40:  rot: 2c974ebe sub: 71882fae rcon: 36000000 xor: ae2f8847 rs: 13111d7f
    41:  equ: 13111d7f rs: e3944a17
    42:  equ: e3944a17 rs: f307a78b
    43:  equ: f307a78b rs: 4d2b30c5

加密過程例項

Encrypting block ...
 Round 0:
   input:  00 11 22 33 44 55 66 77 88 99 aa bb cc dd ee ff
   round:  00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f
   state:  00 10 20 30 40 50 60 70 80 90 a0 b0 c0 d0 e0 f0
 Round 1:
   input:  00 10 20 30 40 50 60 70 80 90 a0 b0 c0 d0 e0 f0
     sub:  63 ca b7 04 09 53 d0 51 cd 60 e0 e7 ba 70 e1 8c
   shift:  63 53 e0 8c 09 60 e1 04 cd 70 b7 51 ba ca d0 e7
     mix:  5f 72 64 15 57 f5 bc 92 f7 be 3b 29 1d b9 f9 1a
   round:  d6 aa 74 fd d2 af 72 fa da a6 78 f1 d6 ab 76 fe
   state:  89 d8 10 e8 85 5a ce 68 2d 18 43 d8 cb 12 8f e4
 Round 2:
   input:  89 d8 10 e8 85 5a ce 68 2d 18 43 d8 cb 12 8f e4
     sub:  a7 61 ca 9b 97 be 8b 45 d8 ad 1a 61 1f c9 73 69
   shift:  a7 be 1a 69 97 ad 73 9b d8 c9 ca 45 1f 61 8b 61
     mix:  ff 87 96 84 31 d8 6a 51 64 51 51 fa 77 3a d0 09
   round:  b6 92 cf 0b 64 3d bd f1 be 9b c5 00 68 30 b3 fe
   state:  49 15 59 8f 55 e5 d7 a0 da ca 94 fa 1f 0a 63 f7
 Round 3:
   input:  49 15 59 8f 55 e5 d7 a0 da ca 94 fa 1f 0a 63 f7
     sub:  3b 59 cb 73 fc d9 0e e0 57 74 22 2d c0 67 fb 68
   shift:  3b d9 22 68 fc 74 fb 73 57 67 cb e0 c0 59 0e 2d
     mix:  4c 9c 1e 66 f7 71 f0 76 2c 3f 86 8e 53 4d f2 56
   round:  b6 ff 74 4e d2 c2 c9 bf 6c 59 0c bf 04 69 bf 41
   state:  fa 63 6a 28 25 b3 39 c9 40 66 8a 31 57 24 4d 17
 Round 4:
   input:  fa 63 6a 28 25 b3 39 c9 40 66 8a 31 57 24 4d 17
     sub:  2d fb 02 34 3f 6d 12 dd 09 33 7e c7 5b 36 e3 f0
   shift:  2d 6d 7e f0 3f 33 e3 34 09 36 02 dd 5b fb 12 c7
     mix:  63 85 b7 9f fc 53 8d f9 97 be 47 8e 75 47 d6 91
   round:  47 f7 f7 bc 95 35 3e 03 f9 6c 32 bc fd 05 8d fd
   state:  24 72 40 23 69 66 b3 fa 6e d2 75 32 88 42 5b 6c
 Round 5:
   input:  24 72 40 23 69 66 b3 fa 6e d2 75 32 88 42 5b 6c
     sub:  36 40 09 26 f9 33 6d 2d 9f b5 9d 23 c4 2c 39 50
   shift:  36 33 9d 50 f9 b5 39 26 9f 2c 09 2d c4 40 6d 23
     mix:  f4 bc d4 54 32 e5 54 d0 75 f1 d6 c5 1d d0 3b 3c
   round:  3c aa a3 e8 a9 9f 9d eb 50 f3 af 57 ad f6 22 aa
   state:  c8 16 77 bc 9b 7a c9 3b 25 02 79 92 b0 26 19 96
 Round 6:
   input:  c8 16 77 bc 9b 7a c9 3b 25 02 79 92 b0 26 19 96
     sub:  e8 47 f5 65 14 da dd e2 3f 77 b6 4f e7 f7 d4 90
   shift:  e8 da b6 90 14 77 d4 65 3f f7 f5 e2 e7 47 dd 4f
     mix:  98 16 ee 74 00 f8 7f 55 6b 2c 04 9c 8e 5a d0 36
   round:  5e 39 0f 7d f7 a6 92 96 a7 55 3d c1 0a a3 1f 6b
   state:  c6 2f e1 09 f7 5e ed c3 cc 79 39 5d 84 f9 cf 5d
 Round 7:
   input:  c6 2f e1 09 f7 5e ed c3 cc 79 39 5d 84 f9 cf 5d
     sub:  b4 15 f8 01 68 58 55 2e 4b b6 12 4c 5f 99 8a 4c
   shift:  b4 58 12 4c 68 b6 8a 01 4b 99 f8 2e 5f 15 55 4c
     mix:  c5 7e 1c 15 9a 9b d2 86 f0 5f 4b e0 98 c6 34 39
   round:  14 f9 70 1a e3 5f e2 8c 44 0a df 4d 4e a9 c0 26
   state:  d1 87 6c 0f 79 c4 30 0a b4 55 94 ad d6 6f f4 1f
 Round 8:
   input:  d1 87 6c 0f 79 c4 30 0a b4 55 94 ad d6 6f f4 1f
     sub:  3e 17 50 76 b6 1c 04 67 8d fc 22 95 f6 a8 bf c0
   shift:  3e 1c 22 c0 b6 fc bf 76 8d a8 50 67 f6 17 04 95
     mix:  ba a0 3d e7 a1 f9 b5 6e d5 51 2c ba 5f 41 4d 23
   round:  47 43 87 35 a4 1c 65 b9 e0 16 ba f4 ae bf 7a d2
   state:  fd e3 ba d2 05 e5 d0 d7 35 47 96 4e f1 fe 37 f1
 Round 9:
   input:  fd e3 ba d2 05 e5 d0 d7 35 47 96 4e f1 fe 37 f1
     sub:  54 11 f4 b5 6b d9 70 0e 96 a0 90 2f a1 bb 9a a1
   shift:  54 d9 90 a1 6b a0 9a b5 96 bb f4 0e a1 11 70 2f
     mix:  e9 f7 4e ec 02 30 20 f6 1b f2 cc f2 35 3c 21 c7
   round:  54 99 32 d1 f0 85 57 68 10 93 ed 9c be 2c 97 4e
   state:  bd 6e 7c 3d f2 b5 77 9e 0b 61 21 6e 8b 10 b6 89
 Round 10:
   input:  bd 6e 7c 3d f2 b5 77 9e 0b 61 21 6e 8b 10 b6 89
     sub:  7a 9f 10 27 89 d5 f5 0b 2b ef fd 9f 3d ca 4e a7
   shift:  7a d5 fd a7 89 ef 4e 27 2b ca 10 0b 3d 9f f5 9f
   round:  13 11 1d 7f e3 94 4a 17 f3 07 a7 8b 4d 2b 30 c5
   state:  69 c4 e0 d8 6a 7b 04 30 d8 cd b7 80 70 b4 c5 5a
Output:
  cypher:  69 c4 e0 d8 6a 7b 04 30 d8 cd b7 80 70 b4 c5 5a

解密輪函式

對Rijndael演算法來說解密過程就是加密過程的逆向過程，其解密輪函式實現如下：

int aes_decrypt(AES_CYPHER_T mode, uint8_t *data, int len, uint8_t *key)
{
    uint8_t w[4 * 4 * 15] = {0}; /* round key */
    uint8_t s[4 * 4] = {0}; /* state */

    int nr, i, j;

    /* key expansion */
    aes_key_expansion(mode, key, w);

    /* start data cypher loop over input buffer */
    for (i = 0; i < len; i += 4 * g_aes_nb[mode]) {

        /* init state from user buffer (cyphertext) */
        for (j = 0; j < 4 * g_aes_nb[mode]; j++)
            s[j] = data[i + j];

        /* start AES cypher loop over all AES rounds */
        for (nr = g_aes_rounds[mode]; nr >= 0; nr--) {

            /* do AddRoundKey */
            aes_add_round_key(mode, s, w, nr);

            if (nr > 0) {
                if (nr < g_aes_rounds[mode]) {
                    /* do MixColumns */
                    inv_mix_columns(mode, s);
                }

                /* do ShiftRows */
                inv_shift_rows(mode, s);

                /* do SubBytes */
                inv_sub_bytes(mode, s);
            }
        }

        /* save state (cypher) to user buffer */
        for (j = 0; j < 4 * g_aes_nb[mode]; j++)
            data[i + j] = s[j];
    }

    return 0;
}

解密過程例項

Decrypting block ...
 Round 10:
   input:  69 c4 e0 d8 6a 7b 04 30 d8 cd b7 80 70 b4 c5 5a
   round:  13 11 1d 7f e3 94 4a 17 f3 07 a7 8b 4d 2b 30 c5
   shift:  7a d5 fd a7 89 ef 4e 27 2b ca 10 0b 3d 9f f5 9f
     sub:  7a 9f 10 27 89 d5 f5 0b 2b ef fd 9f 3d ca 4e a7
   state:  bd 6e 7c 3d f2 b5 77 9e 0b 61 21 6e 8b 10 b6 89
 Round 9:
   input:  bd 6e 7c 3d f2 b5 77 9e 0b 61 21 6e 8b 10 b6 89
   round:  54 99 32 d1 f0 85 57 68 10 93 ed 9c be 2c 97 4e
     mix:  e9 f7 4e ec 02 30 20 f6 1b f2 cc f2 35 3c 21 c7
   shift:  54 d9 90 a1 6b a0 9a b5 96 bb f4 0e a1 11 70 2f
     sub:  54 11 f4 b5 6b d9 70 0e 96 a0 90 2f a1 bb 9a a1
   state:  fd e3 ba d2 05 e5 d0 d7 35 47 96 4e f1 fe 37 f1
 Round 8:
   input:  fd e3 ba d2 05 e5 d0 d7 35 47 96 4e f1 fe 37 f1
   round:  47 43 87 35 a4 1c 65 b9 e0 16 ba f4 ae bf 7a d2
     mix:  ba a0 3d e7 a1 f9 b5 6e d5 51 2c ba 5f 41 4d 23
   shift:  3e 1c 22 c0 b6 fc bf 76 8d a8 50 67 f6 17 04 95
     sub:  3e 17 50 76 b6 1c 04 67 8d fc 22 95 f6 a8 bf c0
   state:  d1 87 6c 0f 79 c4 30 0a b4 55 94 ad d6 6f f4 1f
 Round 7:
   input:  d1 87 6c 0f 79 c4 30 0a b4 55 94 ad d6 6f f4 1f
   round:  14 f9 70 1a e3 5f e2 8c 44 0a df 4d 4e a9 c0 26
     mix:  c5 7e 1c 15 9a 9b d2 86 f0 5f 4b e0 98 c6 34 39
   shift:  b4 58 12 4c 68 b6 8a 01 4b 99 f8 2e 5f 15 55 4c
     sub:  b4 15 f8 01 68 58 55 2e 4b b6 12 4c 5f 99 8a 4c
   state:  c6 2f e1 09 f7 5e ed c3 cc 79 39 5d 84 f9 cf 5d
 Round 6:
   input:  c6 2f e1 09 f7 5e ed c3 cc 79 39 5d 84 f9 cf 5d
   round:  5e 39 0f 7d f7 a6 92 96 a7 55 3d c1 0a a3 1f 6b
     mix:  98 16 ee 74 00 f8 7f 55 6b 2c 04 9c 8e 5a d0 36
   shift:  e8 da b6 90 14 77 d4 65 3f f7 f5 e2 e7 47 dd 4f
     sub:  e8 47 f5 65 14 da dd e2 3f 77 b6 4f e7 f7 d4 90
   state:  c8 16 77 bc 9b 7a c9 3b 25 02 79 92 b0 26 19 96
 Round 5:
   input:  c8 16 77 bc 9b 7a c9 3b 25 02 79 92 b0 26 19 96
   round:  3c aa a3 e8 a9 9f 9d eb 50 f3 af 57 ad f6 22 aa
     mix:  f4 bc d4 54 32 e5 54 d0 75 f1 d6 c5 1d d0 3b 3c
   shift:  36 33 9d 50 f9 b5 39 26 9f 2c 09 2d c4 40 6d 23
     sub:  36 40 09 26 f9 33 6d 2d 9f b5 9d 23 c4 2c 39 50
   state:  24 72 40 23 69 66 b3 fa 6e d2 75 32 88 42 5b 6c
 Round 4:
   input:  24 72 40 23 69 66 b3 fa 6e d2 75 32 88 42 5b 6c
   round:  47 f7 f7 bc 95 35 3e 03 f9 6c 32 bc fd 05 8d fd
     mix:  63 85 b7 9f fc 53 8d f9 97 be 47 8e 75 47 d6 91
   shift:  2d 6d 7e f0 3f 33 e3 34 09 36 02 dd 5b fb 12 c7
     sub:  2d fb 02 34 3f 6d 12 dd 09 33 7e c7 5b 36 e3 f0
   state:  fa 63 6a 28 25 b3 39 c9 40 66 8a 31 57 24 4d 17
 Round 3:
   input:  fa 63 6a 28 25 b3 39 c9 40 66 8a 31 57 24 4d 17
   round:  b6 ff 74 4e d2 c2 c9 bf 6c 59 0c bf 04 69 bf 41
     mix:  4c 9c 1e 66 f7 71 f0 76 2c 3f 86 8e 53 4d f2 56
   shift:  3b d9 22 68 fc 74 fb 73 57 67 cb e0 c0 59 0e 2d
     sub:  3b 59 cb 73 fc d9 0e e0 57 74 22 2d c0 67 fb 68
   state:  49 15 59 8f 55 e5 d7 a0 da ca 94 fa 1f 0a 63 f7
 Round 2:
   input:  49 15 59 8f 55 e5 d7 a0 da ca 94 fa 1f 0a 63 f7
   round:  b6 92 cf 0b 64 3d bd f1 be 9b c5 00 68 30 b3 fe
     mix:  ff 87 96 84 31 d8 6a 51 64 51 51 fa 77 3a d0 09
   shift:  a7 be 1a 69 97 ad 73 9b d8 c9 ca 45 1f 61 8b 61
     sub:  a7 61 ca 9b 97 be 8b 45 d8 ad 1a 61 1f c9 73 69
   state:  89 d8 10 e8 85 5a ce 68 2d 18 43 d8 cb 12 8f e4
 Round 1:
   input:  89 d8 10 e8 85 5a ce 68 2d 18 43 d8 cb 12 8f e4
   round:  d6 aa 74 fd d2 af 72 fa da a6 78 f1 d6 ab 76 fe
     mix:  5f 72 64 15 57 f5 bc 92 f7 be 3b 29 1d b9 f9 1a
   shift:  63 53 e0 8c 09 60 e1 04 cd 70 b7 51 ba ca d0 e7
     sub:  63 ca b7 04 09 53 d0 51 cd 60 e0 e7 ba 70 e1 8c
   state:  00 10 20 30 40 50 60 70 80 90 a0 b0 c0 d0 e0 f0
 Round 0:
   input:  00 10 20 30 40 50 60 70 80 90 a0 b0 c0 d0 e0 f0
   round:  00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f
   state:  00 11 22 33 44 55 66 77 88 99 aa bb cc dd ee ff
Output:
   plain:  00 11 22 33 44 55 66 77 88 99 aa bb cc dd ee ff

演算法設計思想

加密演算法的一般設計準則

• 混淆 (Confusion) 最大限度地複雜化密文、明文與金鑰之間的關係，通常用非線性變換演算法達到最大化的混淆。
• 擴散 (Diffusion) 明文或金鑰每變動一位將最大化地影響密文中的位數，通常採用線性變換演算法達到最大化的擴散。

AES評判要求

NIST在徵集演算法的時候就提出了幾項硬性要求：

• 分組加密演算法：支援128位分組大小，128/192/256位金鑰
• 安全性不低於3DES，但實施與執行要比3DES的更高效
• 優化過的ANSI C的實現程式碼
• KAT(Known-Answer tests)及MCT(Monte Carlo Tests)測試及驗證
• 軟體及硬體實現的便捷
• 可抵禦已知攻擊

Rijndael設計思想

1. 安全性（Security） 演算法足夠強，抗攻擊
2. 經濟性（Efficiency） 演算法運算效率高
3. 金鑰捷變（Key Agility） 更改金鑰所引入的損失儘量小，即最小消耗的金鑰擴充套件演算法
4. 適應性 （Versatility） 適用於不同的CPU架構，軟體或硬體平臺的實現
5. 設計簡單（Simplicity） 輪函式的設計精簡，只是多輪迭代

S盒設計

S盒是由一個有限域GF(256)上的乘法求逆並串聯線性仿射變換所構造出來的，不是一個隨意構造的簡單查詢表。因其運算複雜，眾多的AES 軟體及硬體實現直接使用了查詢表(LUP, Look-up table)，但查詢表的方式並不適合所有場景，針對特定的硬體最小化面積設計需求，則要採用優化的組合邏輯以得到同價的S盒替換。

工作模式

分組加密演算法是按分組大小來進行加解密操作的，如DES演算法的分組是64位，而AES是128位，但實際明文的長度一般要遠大於分組大小，這樣的情況如何處理呢？

這正是"mode of operation"即工作模式要解決的問題：明文資料流怎樣按分組大小切分，資料不對齊的情況怎麼處理等等。

早在1981年，DES演算法公佈之後，NIST在標準文獻FIPS 81中公佈了4種工作模式：

• 電子密碼本：Electronic Code Book Mode (ECB)

• 密碼分組連結：Cipher Block Chaining Mode (CBC)

• 密文反饋：Cipher Feedback Mode (CFB)

• 輸出反饋：Output Feedback Mode (OFB)

2001年又針對AES加入了新的工作模式：

• 計數器模式：Counter Mode (CTR)

後來又陸續引入其它新的工作模式。在此僅介紹幾種常用的：

ECB：電子密碼本模式

ECB模式只是將明文按分組大小切分，然後用同樣的金鑰正常加密切分好的明文分組。

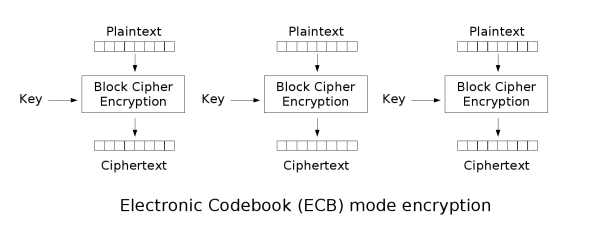
ECB的理想應用場景是短資料（如加密金鑰）的加密。此模式的問題是無法隱藏原明文資料的模式，因為同樣的明文分組加密得到的密文也是一樣的。

舉例來說明，下圖為明文圖片：

經ECB模式加密的圖片：圖中也正好驗證了AES的擴散效果：作為區域性圖案的葉子，其紅顏色在加密後擴散到了整張圖片上。

經CBC模式加密的圖片：

CBC：密碼分組連結模式

此模式是1976年由IBM所發明，引入了IV（初始化向量：Initialization Vector）的概念。IV是長度為分組大小的一組隨機，通常情況下不用保密，不過在大多數情況下，針對同一金鑰不應多次使用同一組IV。 CBC要求第一個分組的明文在加密運算前先與IV進行異或；從第二組開始，所有的明文先與前一分組加密後的密文進行異或。[區塊鏈(blockchain)的鼻祖！]

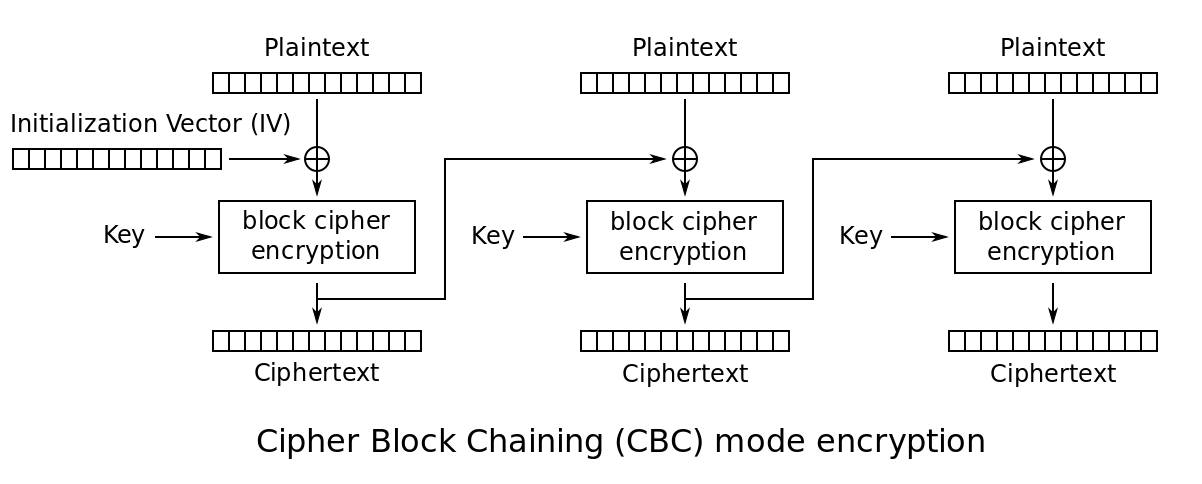
CBC模式相比ECB實現了更好的模式隱藏，但因為其將密文引入運算，加解密操作無法並行操作。同時引入的IV向量，還需要加、解密雙方共同知曉方可。

實現程式碼：

int aes_encrypt_cbc(AES_CYPHER_T mode, uint8_t *data, int len,
                    uint8_t *key, uint8_t *iv)
{
    uint8_t w[4 * 4 * 15] = {0}; /* round key */
    uint8_t s[4 * 4] = {0}; /* state */
    uint8_t v[4 * 4] = {0}; /* iv */

    int nr, i, j;

    /* key expansion */
    aes_key_expansion(mode, key, w);
    memcpy(v, iv, sizeof(v));

    /* start data cypher loop over input buffer */
    for (i = 0; i < len; i += 4 * g_aes_nb[mode]) {
        /* init state from user buffer (plaintext) */
        for (j = 0; j < 4 * g_aes_nb[mode]; j++)
            s[j] = data[i + j] ^ v[j];

        /* start AES cypher loop over all AES rounds */
        for (nr = 0; nr <= g_aes_rounds[mode]; nr++) {

            if (nr > 0) {

                /* do SubBytes */
                aes_sub_bytes(mode, s);

                /* do ShiftRows */
                aes_shift_rows(mode, s);

                if (nr < g_aes_rounds[mode]) {
                    /* do MixColumns */
                    aes_mix_columns(mode, s);
                }
            }

            /* do AddRoundKey */
            aes_add_round_key(mode, s, w, nr);
        }

        /* save state (cypher) to user buffer */
        for (j = 0; j < 4 * g_aes_nb[mode]; j++)
            data[i + j] = v[j] = s[j];
    }

    return 0;
}

CFB：密文反饋模式

與CBC模式類似，但不同的地方在於，CFB模式先生成密碼流字典，然後用密碼字典與明文進行異或操作並最終生成密文。後一分組的密碼字典的生成需要前一分組的密文參與運算。

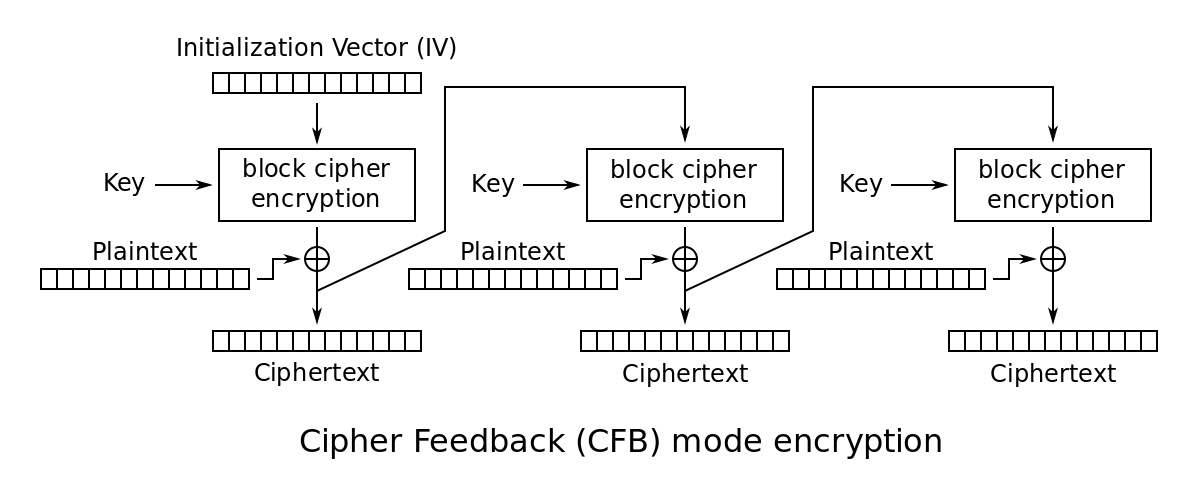
CFB模式是用分組演算法實現流演算法，明文資料不需要按分組大小對齊。

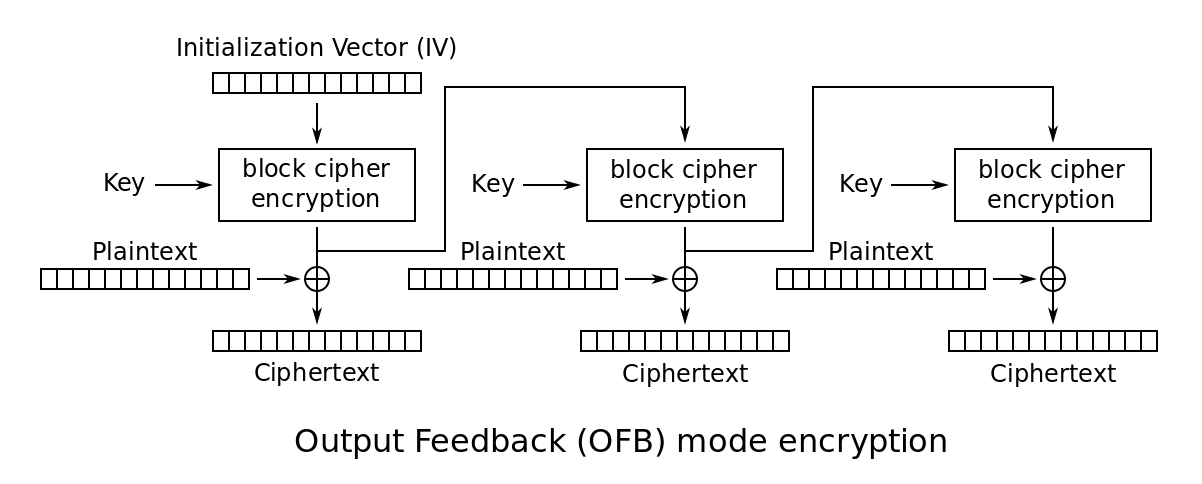
OFB：輸出反饋模式

OFB模式與CFB模式不同的地方是：生成字典的時候會採用明文參與運算，CFB採用的是密文。

CTR：計數器模式模式

CTR模式同樣會產生流密碼字典，但同是會引入一個計數，以保證任意長時間均不會產生重複輸出。

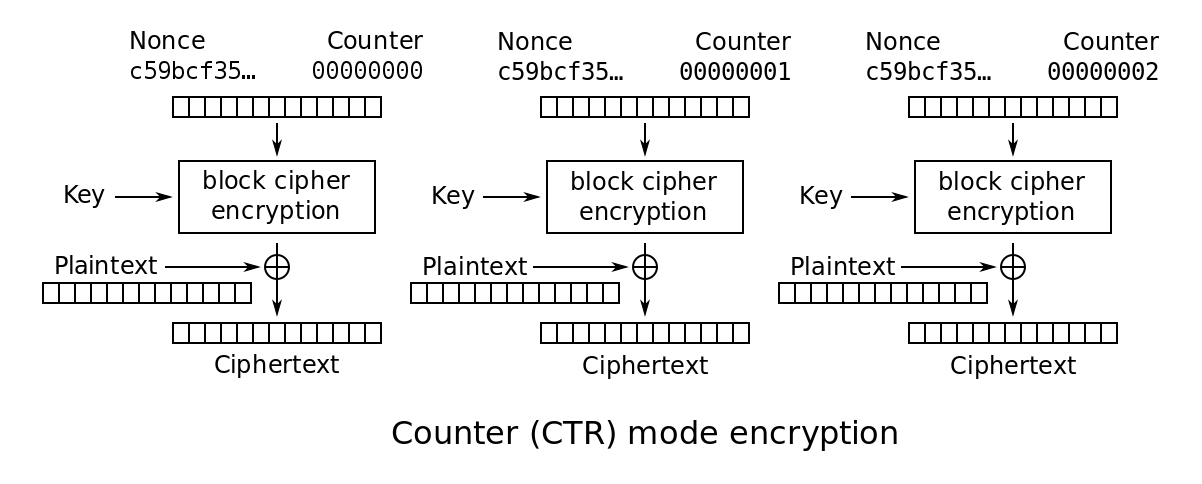
CTR模式只需要實現加密演算法以生成字典，明文資料與之異或後得到密文，反之便是解密過程。CTR模式可以採用並行演算法處理以提升吞量，另外加密資料塊的訪問可以是隨機的，與前後上下文無關。

CCM：Counter with CBC-MAC

CCM模式，全稱是Counter with Cipher Block Chaining-Message Authentication Code，是CTR工作模式和CMAC認證演算法的組合體，可以同時資料加密和鑑別服務。

明文資料通過CTR模式加密成密文，然後在密文後面再附加上認證資料，所以最終的密文會比明文要長。具體的加密流程如下描述：先對明文資料認證併產生一個tag，在後續加密過程中使用此tag和IV生成校驗值U。然後用CTR模式來加密原輸入明文資料，在密文的後面附上校驗碼Ｕ。

GCM：伽羅瓦計數器模式

型別CCM模式，GCM模式是CTR和GHASH的組合，GHASH操作定義為密文結果與金鑰以及訊息長度在GF（2^128）域上相乘。GCM比CCM的優勢是在於更高並行度及更好的效能。TLS 1.2標準使用的就是AES-GCM演算法，並且Intel CPU提供了GHASH的硬體加速功能。

硬體加速

AES作為主導的加密標準，其應用越來越廣泛，特別是針對網路資料的加密需求，越來越多的硬體都整合AES 128/192/256位演算法及不同的工作模式的硬體加速的實現。

AES_NI: X86架構

Intel於2010發發布了支援AES加速的CPU，實現了高階的AES加解密指令即AES_NI：AES New Instructions。AES_NI包含6指令：其中4條用於加解密，2條用於金鑰擴充套件。根據AES_NI白皮書中所說，AES_NI可以帶來2-3倍的效能提升。

Instruction	Description
AESENC	Perform one round of an AES encryption flow
AESENCLAST	Perform the last round of an AES encryption flow
AESDEC	Perform one round of an AES decryption flow
AESDECLAST	Perform the last round of an AES decryption flow
AESKEYGENASSIST	Assist in AES round key generation
AESIMC	Assist in AES Inverse Mix Columns

目前OpenSSL，Linux's Crypto API以及Windows Cryptography API中均已加入對AES_NI的支援。

AES_NI: 測試

測試環境：

Intel(R) Core(TM) i7-4790 CPU @ 3.60GHz 4 Cores with HyperThread (Enabled or Disabled)
Ubuntu 16.04 AMD64, OpenSSL 1.0.2g-fips  1 Mar 2016

測試方法：

關閉硬體加速1/2/4/8執行緒AES-256/128-CBC：
OPENSSL_ia32cap="~0x200000200000000" openssl speed -multi {1/2/4/8} -elapsed -evp {aes-256/128-cbc}

開啟硬體加速1/2/4/8執行緒AES-256/128-CBC：
openssl speed -multi {1/2/4/8} -elapsed -evp {aes-256/128-cbc}

超執行緒的開戶與關閉只能通過UEFI/BIOS來設定，測試命令同上。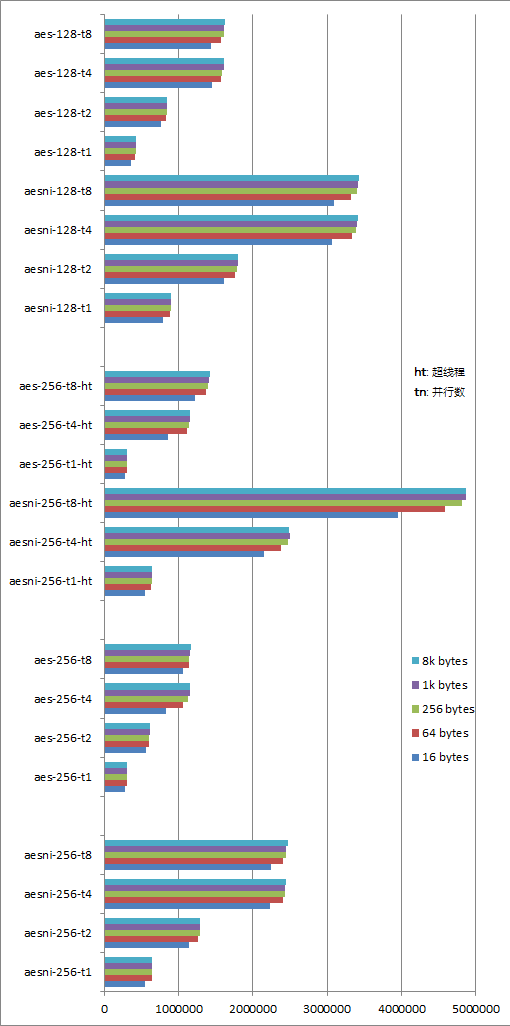

從圖中可以得到如下結論：

1. AES_NI加速可以提升效能1倍多，AESNI-128基本上都是AES-128的2.2倍左右。
2. AES-128與AES-256的效能比基本在1.36左右（15/11，忽略金鑰編排用時的情況下）
3. 比較有趣的一點發現是，超執行緒所帶來的影響比預想的要大得多。針對高並行的情形，在開啟AES_NI時超執行緒可以帶來接近1倍的效能提升；但在關閉AES_NI的情況下對效能提升的貢獻要小的多。超執行緒雖然邏輯上讓我們覺得一核變成了兩核，其實質只是同一物理核上的佇列管理機制，關閉AES_NI的情況下的測試資料基本驗證了這一點。另一方面AES_NI硬體加速是基於物理核的，不可能是針對超執行緒的，所以超執行緒與AES_NI組合所帶來的巨大的效能提升讓人有些費解，比較可能的解釋是AES_NI硬體加速引擎的潛力足夠強大以至於一個物理核心不能完全發揮其效能，所以在超執行緒開啟的情況下能有更好的表現。

ARM及其它體系

2011年釋出的ARMv8-A處理器架構開始支援AES加速指令，其指令集與AES_NI不相容但實現了類似的功能。除ARM外，SUN SPARC(T4, T5, M5以後)及IBM Power7+架構的CPU均已支援AES加速。

實現上的安全性考慮

記憶體與交換

程式如果將金鑰儲存在可交換記憶體頁中，在記憶體吃緊的情況下有可能會交換出來並寫入磁碟。如輔以程式碼逆向等，金鑰很有可能會洩露。

應用層最好用mlock(Linux)或VirtualLock(Windows)來防止記憶體頁被交換至磁碟。

但因為金鑰在記憶體中，所以任何能訪問記憶體的方式均有可能導致金鑰的洩漏。曾流行的一種攻擊是通過1394 DMA方式來訪問目標機記憶體，Linux/Windows Login bypass，Windows bitlock等漏洞均由起引起。較新的CPU為硬體虛擬化所引入的IO MMU （Intel VT-d or AMD-Vi）可以有效地限制硬體對記憶體的訪問許可權。

傳統攻擊

AES從產生至今依然是最安全的加密演算法，傳統攻擊手段依然無法撼動其安全性。雖然已有攻擊手段顯示可以將AES-256的暴力搜尋次數從2^256次降至2^119次，但依然沒有實際操作價值。

不過隨著計算力的提升，特別是量子計算機的發展，AES將不再是安全的。不過可以肯定的是：一定會出現更安全的加密演算法。

旁路攻擊

旁路攻擊（Side-channel attack, SCA）是指繞過對加密演算法的正面對抗及分析，利用硬體實現加密演算法的邏輯電路在運算中所洩露的資訊，如執行時間、功耗、電磁輻射等，並結合統計理論來實現對密碼系統攻擊的手段。

旁路攻擊條件

旁路攻擊成功的必要條件：

1. 在洩漏的物理訊號與處理的資料之間建立關聯
2. 在資訊洩漏模型中處理的資料與晶片中處理的資料之間建立關聯

智慧卡CPU的實現邏輯相對比較簡單，並且都是單執行緒處理機制，因此可以很好的建立起密碼-時序或密碼-功耗之間的關聯。

時序攻擊

不同的數值及不同的運算所需時間是不同的，在演算法(運算邏輯)固定的前提下完全可以根據執行時間反推出具體的運算元。舉個簡單的例子：

if (strelen(passwd) != sizeof(fixed_passwd))
  return 0;

for (i = 0; i < sizeof(fixed_passwd); i++)
  if (passwd[i] != fixed_passwd[i])
    return 0;

這段程式碼在密碼的判斷上就存在時序攻擊的漏洞，如果第一個字元不匹配則直接退出，只有在當前字元匹配的情況下才會繼續下一個字元的比較。

所以如果實際密碼長度為8位且只能用字母及數字，則理論上暴力搜尋次數為 (26 2 + 10) ^ 8。但因為演算法的實現沒有考慮到時序攻擊，如果將執行時間加入考量，則搜尋次數將降低至(26 2 + 10) * 8。

本文示例程式碼中aes_mul()的實現也有時序攻擊的漏洞，並且實現效率也比較低，當然主要目的是為了演算法演示。

功耗攻擊

當訊號發生0-1跳變時，需要電源對電容進行充電；而在其它三種情況(0-0, 1-1, 1-0)下則不會進行充電操作，因此可以很容易區分出前者來，這就是功耗攻擊原理的簡單解釋。

功耗攻擊一般分為簡單功耗攻擊(Simple Power Analysis，SPA)，差分功耗攻擊(Differential Power Analysis, DPA)，高階DPA等。SPA可以揭示出執行操作和能耗洩露間的關係，而DPA則能夠揭示出處理資料和能耗洩露間的關係。

DPA利用不同資料對應的條件功耗分佈的差異進行統計分析以找出數值與功耗的微弱關聯性，並利用此關聯性極大的降低金鑰的搜尋空間，進而完成高效且低成本的攻擊。

上海交大的教授鬱昱就通過功耗攻擊成功破解了來自多家手機制造商以及服務供應商的SIM卡的金鑰。更詳細資訊可見於他在Blackhat 2015年的演示稿: Cloning 3G/4G SIM Cards with a PC and an Oscilloscope: Lessons Learned in Physical Security。

以色列特拉維夫大學的研究人員利用旁路攻擊，成功從Android和iOS裝置上竊取到用於加密比特幣錢包、Apple Pay賬號和其他高價值資產的金鑰，詳細請參閱論文: ECDSA Key Extraction from Mobile Devices via Nonintrusive Physical Side Channels。

參考資料

1. 密碼學原理與實踐(第二版)，Douglas R. Stinson，馮登國譯
2. AES Proposal: Rijndael by Joan Daemen and Vincent Rijmen
3. FIPS 197: Announcing the AES
4. Advanced Encryption Standard - Wikipedia
5. The Design of Rijndael by Joan Daemen & Vincent Rijmen
6. The Block Cipher Companion, L. Knudsen & M. Robshaw, 2011
7. 加密晶片的旁道攻擊防禦對策研究(博士學位論文), 李海軍, 2008
8. 旁路之能量分析攻擊總結
9. AES演算法介紹: 萬天添，2015/3/23
10. AES_NI - Wikipedia
11. AES_NI v3.01 - Intel

相關程式碼

1. https://github.com/matt-wu/AES/

<最早的手工計算AES-128的想法源於2016年底讀過的一本書《How Software Works: The Magic Behind Encryption ...》，在閱讀過程中發現AES一節中的資料全對不上，然後於17年初開始翻閱AES及Rijndael演算法標準等資料，等看完所有文件後才發現此書對AES的介紹真是簡化得沒邊了，後來又做了大量的延伸閱讀，春節期間根據FIPS 197及《The Design of Rijndael》實現了AES 128/192/256 ECB/CBC的計算過程，之後開始本blog的書寫，中間斷斷續續直至今日才完工，本文估計用時約40小時。學習從來不是容易的事！但越是不容易的事情做起來才更有樂趣！>