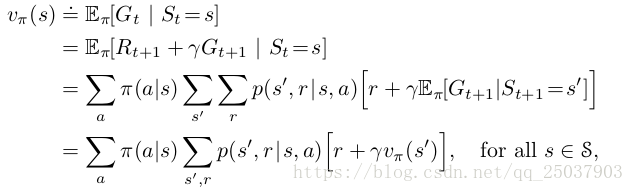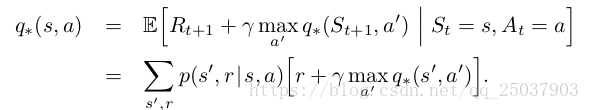強化學習(RLAI)讀書筆記第三章有限馬爾科夫決策過程(finite MDP)
第三章 有限馬爾科夫決策過程
有限馬爾科夫決策過程(MDP)是關於評估型反饋的,就像多臂老虎機問題裡一樣,但是有是關聯型的問題。MDP是一個經典的關於連續序列決策的模型,其中動作不僅影響當前的反饋,也會影響接下來的狀態以及以後的反饋。因此MDP需要考慮延遲反饋和當前反饋與延遲反饋之間的交換。
MDP是強化學習問題的一個數學理想化模型,以此來精確地從理論上描述。這章將會介紹強化學習裡的一些關鍵問題,比如反饋reward,值函式value function和Bellman方程。
3.1 The Agent-Environment Interface
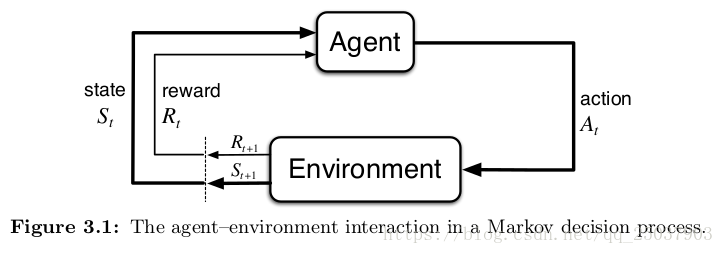
MDPs是一個從互動中達成目標的強化學習問題的一個直接的框架。學習者和決策者叫做agent。agent進行互動的其它一切agent之外的東西都叫做環境。agent不斷的選擇動作,而環境也給出相應的反應,並且向agent表現出新的狀態。環境同時也給出一個數值作為反饋。agent的目標就是通過選擇不同的action來最大化這個反饋值。
具體地說,agent和環境在每個離散時間步驟進行互動,t=1,2,。。。 每個時間步驟tagent會接收到環境的當前狀態並且在狀態的基礎上選擇動作
。每一個步驟之後,作為動作的一個結果,agent會接收到一個數值反饋
,並且會發現自己進入一個新的狀態裡,
。
在有限MDP中,狀態動作和反饋值都只有有限個元素。在這種情況下反饋和狀態
有一個只關於前一狀態以及前一狀態採取的動作的概率分佈:
。這個函式定義出了MDP的動態變化。這個函式對於狀態和反饋值求和之後得到1。函式代表的是,下一個狀態
概率分佈函式p可以計算出關於環境的所有概率,比如狀態轉移概率:
同樣也可以計算出每個狀態動作對的反饋期望:
其中第一個四個引數的概率分佈是我們最常使用的。
MDP框架是一個非常抽象而靈活的應用框架,可以通過不同方式用到不同問題上。比如,時間步驟不一定非得是固定間隔的,可以使任意需要作出決策的連續序列。動作可以使低層次的控制比如電壓控制,也可以是高層次的決策比如去哪裡吃飯。同樣狀態也可以是各種表現形式,動作也是一樣。
需要注意的是,agent和環境之間的界限不是一成不變的。一般來說這個界限靠的離agent更近一些,可能與物理上機器人的界限不太一樣。比如感測器和電機控制部分可以被認為是環境的一部分而非agent。其中劃分的準則是任何不能被agent隨意改變的部分都屬於環境。比如agent可能知道每次reward是如何被反饋來的,但是reward的計算部分被認為在agent之外,因為agent不能隨意改變它。agent與環境的界限代表的是agent的絕對控制,而不是瞭解。
而且這個界限也可以根據不同的任務目標進行調整。在一個複雜的機器人裡面可能有不同的agent在同時執行。
MDP框架是一個非常抽象的目標導向的框架。它致力於把任務中所有的資訊都歸約為在agent與環境之間來回傳播的三個訊號:一是代表agent做出的選擇(action),二是代表做出選擇的基礎(state)以及定義了agent目標的訊號(reward)。對於如何把問題中的各個方面抽象成這些訊號是一個更偏工程的問題,我們目前先關注在這些問題定義好之後的演算法。
練習3.1 空調的控制 下象棋 做飯的火候控制
練習3.2 天氣預報,不僅需要關注今天還需要關注前幾天。
練習3.3 根據目標來決定界限劃分。
練習3.4 只需要把r那一列往前放到一起
3.2 Goals and Rewards
在強化學習中,agent的目標是通過一個特殊的訊號,reward來進行描述的。不正式的說法是agent的目標是最大化它接收到的所有reward的和。也就是說目標不是最大化當前reward而是長期的累計reward。reward訊號的使用是強化學習最重要的特徵之一。儘管這種形式看起來限制很大,但是實際已經證明它很靈活且應用面很廣。
如果我們想要agent完成某件事,那麼一定要把reward定義為agent在完成目標時最大化。所以reward真正反映了任務的目的是一個很重要的事。另外reward不應該是教會agent如何完成目標的地方,reward訊號是告訴agent想要完成什麼而不是如何完成。因此類似於在下棋時給製造出一個陷阱很多reward是不對的。
3.3 Returns and Episodes
我們以及非正式的討論過agent的目標是最大化累積reward。下面介紹這個累積reward的正式定義。大體的說我們尋求最大化反饋的期望值,被定義為反饋序列的某些特殊函式,其中最簡單的定義是
,
T表示的是最後一個時間步。這個定義對於那些能夠自然分成一個個序列的任務很有意義,比如玩一局遊戲或者走一個迷宮等等,每一次都是一個序列。那些有一箇中止狀態的任務被成為episodic tasks。另外有一些沒法分開成一個個序列的任務比如一個機器人整個生命過程,也就是可以被認為時間步驟是無限的任務,叫做continuing tasks。對於這種任務直接把以後所有的reward相加會得到一個無窮值,也就沒法最大化,因此期望值被定義為discounting的形式,即t+1以後每個reward都多加一個[0,1]之間的係數,即:
。
寫為遞推形式為。對於
小於1的情況,如果反饋序列R是有限值,那麼這個無限項相加的結果也是一個有限值。如果每次返回reward的是+1,那麼最終
。
練習3.5 把改為
練習3.6 未失敗返回0,失敗返回-1。 ,k是當前狀態之後的步數。似乎沒啥區別。
練習3.7 沒有辦法找到出口。沒有。
練習3.8 算一下
練習3.9 G1=20 G0=20
練習3.10 等比求和公式
3.4 Unified Notation for Episodic and Continuing Tasks
之前介紹了兩種任務,一種有結束狀態的episodic tasks,另一種是無限狀態的continuing tasks。由於對於episodic tasks來說,每一個episode都是從頭開始,而且屬於哪一個episode並不會影響結果,因此一般忽略關於episode的下標。
為了讓兩種形式的任務的返回值能夠寫成統一的形式,我們把episodic tasks的結束狀態當成一個特殊的無限迴圈狀態,對於到達結束狀態的任務,之後還會無限地返回結束狀態並且返回reward為0。經過這樣的設計,就能夠把兩種任務的反饋期望結合起來寫為統一的形式:
, 其中T可以是無窮,而
可以等於1,但是這兩個條件不能同時滿足。
3.5 Policies and Value Functions
基本所有的強化學習演算法都會評估值函式,也就是評估狀態或者狀態動作對中的agent是否更接近目標。更接近定義為未來反饋值的期望。而值函式是根據某種特殊的動作選擇方式來定義的。這種選擇動作的方式叫做策略(policy)。
正式的policy定義是指從狀態到選擇每個可選動作概率的對映。如果agent在時刻t時遵從policy ,那麼
就是指當
時動作
的概率。
練習3.11
在狀態s時遵循策略的值函式
,是從當前狀態開始遵循策略
之後的反饋值的期望。對於MDPs可以寫成
,
其中是指當agent遵循策略
是對隨機值的期望。如果有結束狀態,那麼結束狀態的值為0。
同樣的我們定義當遵循策略在狀態s時採取了動作a的值
,可以寫成:
,
叫做策略下的動作值函式。
練習3.12
練習3.13
可以從經驗中評估這兩個值函式。比如一個遵循策略的agent為遇到的每一個狀態都保有一個平均反饋值,那麼隨著時間接近無窮大,那麼這個平均值也會逐漸收斂到
,對於
也是一樣的道理。這個方法叫做蒙特卡洛法因為使用了很多隨機樣本真實反饋值的平均。而對於有些問題,狀態太多保持每個狀態的值不太現實,這時候就使用引數化的函式來保持這兩個值函式。
這兩個值函式都可以寫成遞迴的形式,叫做貝爾曼等式(Bellman equation)。對於v的遞推等式如下:
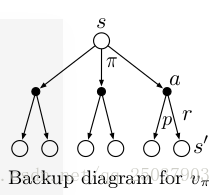
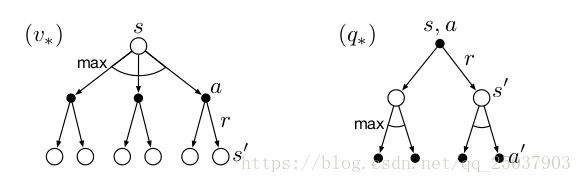
這個過程可以使用一個圖來表示:
在右圖中從頂上的狀態s開始可以在遵循策略下采取集合中的任何動作a。對於每個動作環境都會給出對應的不同反應,也就是轉移到對應的狀態分佈p,並且根據轉移到的狀態s'會返回不同的值r。上述貝爾曼等式就是將不同的動作和對應的轉移狀態分佈的反饋值進行求期望得到的。
對於右圖我們叫做backup diagrams,因為這個圖展示了值函式從後一個狀態往前進行傳遞的過程。另外圖中的狀態不需要是不一樣的,比如每個狀態下一時間可能轉移到這個狀態本身。
練習3.14 0+1/4(2.3+0.4-0.4+0.7) = 0.7
練習3.15 每個v都加了個
,因此不會影響選取動作。
練習3.16 不會有影響。當c大於0就會得到無窮大的反饋,如果c小於0,就會跟不加c一樣。
練習3.17
練習3.18
練習3.19
3.6 Optimal Policies and Optimal Value Functions
解決一個強化學習問題也就是意味著找到一種選擇動作的策略能夠獲得足夠多的獎勵反饋。對於fMDP來說是能夠定義出一個最優策略的。在值函式之上定義一種策略的偏序關係,如果一個策略的所有狀態的值函式都大於策略
,那麼就說前一個策略更好。這樣會有一個最優策略,儘管可能不止一個,我們只用
表示。
這些最優策略有相同的值函式,叫做最優狀態值函式。這個函式被定義為:
。
同樣的也存在一個最優動作值函式:
。
對於狀態動作對(s,a)來說,這個動作值函式給出了在狀態s時採用動作a之後遵循最優策略得到的期望反饋。
。
對於這兩個值函式來說,他們必須滿足上節講到的bellman equation,但是對於最優值函式有獨特的形式,如下:
而對於最優的這兩種情況也有對應的backup diagrams。表示v的圖中在狀態s時選擇最優動作a之後得到反饋然後根據概率分佈轉移到下一個狀態s'。而表示q的圖中在狀態s選擇了動作q之後先根據概率分佈轉移到下一狀態s',然後在狀態s'再選擇其最優動作a'。
對於有限狀態MDP來說,最優貝爾曼方程中v是有一個不依賴於策略的唯一解的。最優貝爾曼方程實際上是一組等式,其中對n個狀態有n個未知數以及n個方程,因此是可解的。只要知道了環境的狀態轉移概率分佈p,就可以直接解出。對q也是一樣。
如果有了最優值,那麼很容易就會選到最優動作和最優策略。可以被看成是一步搜尋,從當前狀態搜尋能夠達到下一最優狀態的動作是什麼。這種策略也叫貪心演算法。對於v來說最好的一點是使用貪心演算法進行一步搜尋最優動作,也就保證了長期的最優,因為值函式v本身就包含了未來動作的反饋期望。而有了最優q函式,我們選擇下一步最優動作時無需考慮接下來的狀態,而是可以直接選擇動作。
直接解貝爾曼最優方程是解決問題的一種方案,但是這種方法很少直接應用。因為這樣做需要進行很多搜尋和觀察所有的可能等等。這個方法需要三個假設:(1)我們準確知道環境的變化(狀態轉移概率分佈);(2)我們有足夠的計算資源直接計算;(3)馬爾科夫性質。一般來說很難三個條件都達到。
但是有很多其他型別的決策性方法被看成是近似解決貝爾曼最優方程的方式,在接下來的章節會講,比如啟發式搜尋,動態規劃等等。
練習3.20 草地外是q(s,driver)的樣子,草地上是v的樣子。
練習3.21 直接是v的樣子不變。
練習3.22 left right 都一樣
練習3.23 太多了。
練習3.24 10+16.0*0.9 = 24.400
練習3.25
練習3.26
練習3.27
練習3.28
練習3.29 略
3.7 Optimality and Approximation
雖然我們已經定義出了最優值函式和最優策略,而且理論上也可以直接計算出來。但是通常情況下我們沒法得到這麼多的計算資源。與此同時記憶體溢位也是一個很大的問題,因為很多問題的狀態數量太多超過儲存範圍。對於這些情況我們就不能夠使用直接儲存每個狀態的值函式而是必須使用一種更精簡的引數型函式表示的方法。
強化學習的框架迫使我們進行近似求解。而且這個框架同時也很容易進行近似,比如對於很多小概率出現的狀態,選擇最優解和次優解區別不大。而且強化學習的線上學習的特性讓其能夠方便地對出現比較多的狀態進行更多關注。這是一個強化學習區分其它近似求解MDP的關鍵特點。
3.8 Summary
強化學習是關於學習如何與環境互動以達成目標的。強化學習的agent和環境在離散時間步驟上進行互動,它們之間的互動定義了一個特定的任務:agent的動作,做出動作的基礎也就是狀態,以及評估每次動作的反饋。agent內部是完全被agent掌控的,在agent之外的都是環境並且可以不完全瞭解。策略是指基於狀態選擇動作的一種隨機規則。agent的目標是最大化所有時間接收到的reward的和。
上面定義的強化學習設定通過一個狀態轉移分佈構成了馬爾科夫決策過程。一個有限狀態MDP是包含有限狀態有限動作和有限reward集合的MDP。很多強化學習的理論侷限於有限狀態MDP,但是很多方法和想法不侷限於此。
反饋值是agent想要最大化的未來獎勵的函式(通過期望值的形式)。根據任務本身的特點和是否使用discounting有不同的定義。不使用discounting的方式適用於episodic tasks,另一種適用於continuing tasks。定義一個特殊狀態可以讓這兩種形式使用同一個等式。
每個狀態的值函式和動作值函式是基於動作或動作狀態對的遵循該策略的未來反饋期望。最優值函式是所有策略中當前狀態能夠獲得的最大反饋期望。取得最優值函式的策略叫做最優策略。貝爾曼最優等式是貝爾曼等式的一個特殊形式,可以得到最優值函式的解。根據最優值函式又能得到最優策略。
根據對整個環境的瞭解又把強化學習問題分為complete knowledge 和 incomplete knowledge兩種。分類標準是agent是否建立起對環境變化的準確而完全的模型。
即使agent擁有完整而準確的環境模型,agent一般也沒有足夠的計算資源去利用它。記憶體也是一個很大的限制,因為很多問題中狀態的數量遠遠超過能夠合理儲存的程度。儘管我們定義了一個最優方案來有利於對強化學習概念的理解,但是現實是很多時候只能對其進行不同程度的近似。強化學習更關注的是那些找不到最優解但是能夠通過一些方式進行近似的例子。