正題

      我就以這一題：玩具裝箱裝玩具來引入我們今天的話題。

      我們先設f[i]表示前i個玩具裝的最小費用是多少。

      那麼，很明顯就有我們列舉一個j，使得j+1到i裝在一起，那麼就有下面的方程。

      然後我們使

      那麼就有

      上面的推導過程是很明顯的。

       接著，我們設

       那麼就有

       我們現在已知，要找到一組x和y使得f[i]最小。

       我們先把a[i]^2丟掉，就剩下：

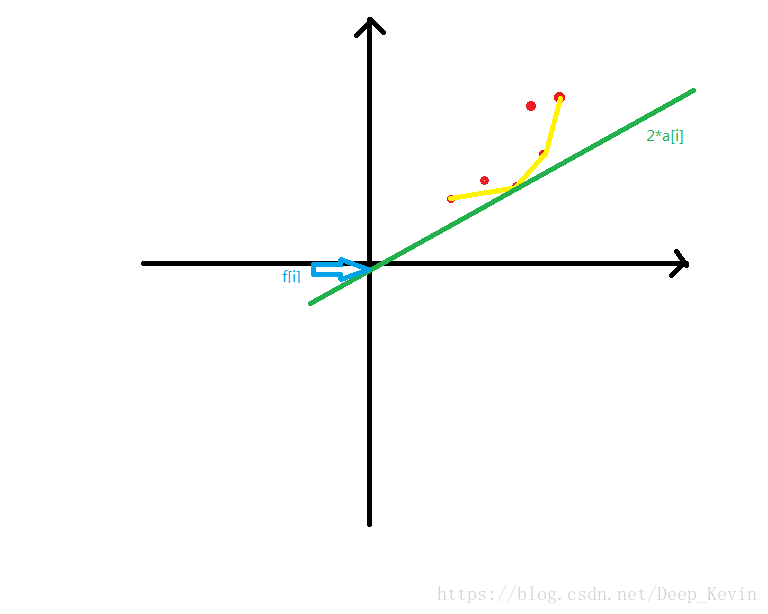
       現在就像一條公式了，所以要使f[i]最小，就相當於讓一條斜率為-k  (2*a[i]) 的直線，從無窮小往上平移，碰到的第一個點就是要求的x和y。明顯這個點肯定在1到i-1的下凸包上，又因為a[i]是遞增的，所以決策一定是單調上升

      那麼證明了決策單調性，可以用常規方法，也可以用維護凸包的方法，維護一下就好了，就像下圖，我們每一次選中的點一定是對於這個斜率的“凸”點。如果有興趣的同學可以用四邊形不等式來證明一下。     

       下面是程式碼，這道題不知道為什麼，算斜率的時候用double是錯的，long long 卻是對的。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int n,m;
long long a[50010],b[50010],f[50010];
struct node{
	long long x,y;
}s[50010],now;
int st=1,ed=1;

long long get_k(node x,node y){
	return (x.y-y.y)/(x.x-y.x);
}

int main(){
	scanf("%d %d",&n,&m);
	int x,sum=0;
	a[0]=0;b[0]=m+1;
	s[st]=(node){b[0],b[0]*b[0]};
	for(int i=1;i<=n;i++){
		scanf("%d",&x);
		sum+=x;
		a[i]=sum+i;b[i]=sum+i+m+1;
	}
	for(int i=1;i<=n;i++){
		while(st<ed && get_k(s[st],s[st+1])<=2*a[i]) st++;
		f[i]=-2*a[i]*s[st].x+s[st].y+a[i]*a[i];
		now=(node){b[i],f[i]+b[i]*b[i]};
		while(st<ed && get_k(s[ed-1],s[ed])>=get_k(s[ed],now)) ed--;
		s[++ed]=now;
	}
	printf("%lld\n",f[n]);
}
 

      有一篇好論文：https://wenku.baidu.com/view/eeb6d3ea19e8b8f67c1cb937.html

      四邊形不等式：如果狀態x轉移到狀態y的代價為w[x,y]，只要滿足

      那麼這個動態規劃問題的決策就是單調的。

      像上面的方程，我們可以把它轉化為

      明顯是狀態i轉移到狀態j的代價，自己動筆，豐衣足食。

      好的，我們現在研究完了這一題，發現什麼，它的是單調上升的，而且斜率也是單調上升的。所以我們可以直接用一個單調佇列來維護下凸包，而不用考慮前面的值。

      現在，我們要研究的問題就是（x單調，k不單調）（x不單調，k單調）和（x不單調，k不單調）三個分支問題。

      我現在只會（x不單調，k不單調）的 O(n log2 n) 的解法，其他的也一樣可以這樣做，但是不知道有沒有特殊的 O(n) 解法。

x不單調，k不單調

       首先我們知道，這種東西會很煩，所以我們就想到了CDQ分治。

       我們先全部按k排序，很明顯k是可以根據輸入直接得到的，並記錄下這個元素原來是在哪裡的。

       每次分，我們把（l , r）區間內的，按原來的位置分成左右兩堆，下去分治。

       先做左邊，每次遞迴結束後會把這些元素按照x座標（算出來的），從左到右排序。

       那麼左邊的序列就是關於x有序的了，我們用左邊的構建一個下凸包，然後用右邊沒有改變過順序的斜率，去更新每一個節點的答案，然後就完了。

       最後把右邊分治一下。遞歸回來之後，把左邊排好序的和右邊排好序的做一次類似於歸併排序的東西就好了。

       例題有[NOI2007]貨幣兌換。

如果多加一維限制，表示x所能取的範圍在之間呢?

       好的，問了一下zhf大佬，是雙log的。

       我們構建一棵線段樹，以位置為關鍵字。每個節點維護一個凸包。

       每次我們對一個節點有一個它的斜率，對於bound[x]~x-1這段區間，線上段樹上是log個的，把它找出來，它肯定是被完全覆蓋的，所以，對於log個區間分別二分就可以了。

       插入一個節點的時候，會更改log個區間，當且僅當這個區間的元素被填滿，我們就把它排序構造一個凸包，那麼插入的時間也是兩個log的。

       這樣子就可以完美得完成這個口胡題。

       以上純屬口胡，要做更多的題，才能完善這個噁心有趣的知識體系。