一：狀壓dp的基本特征

狀態壓縮問題一般是指用十進制的數來表示二進制下的狀態

這種用一個數來表示一組數，以降低表示狀態所需的維數的解題手段，就叫做狀態壓縮。

常用到位運算

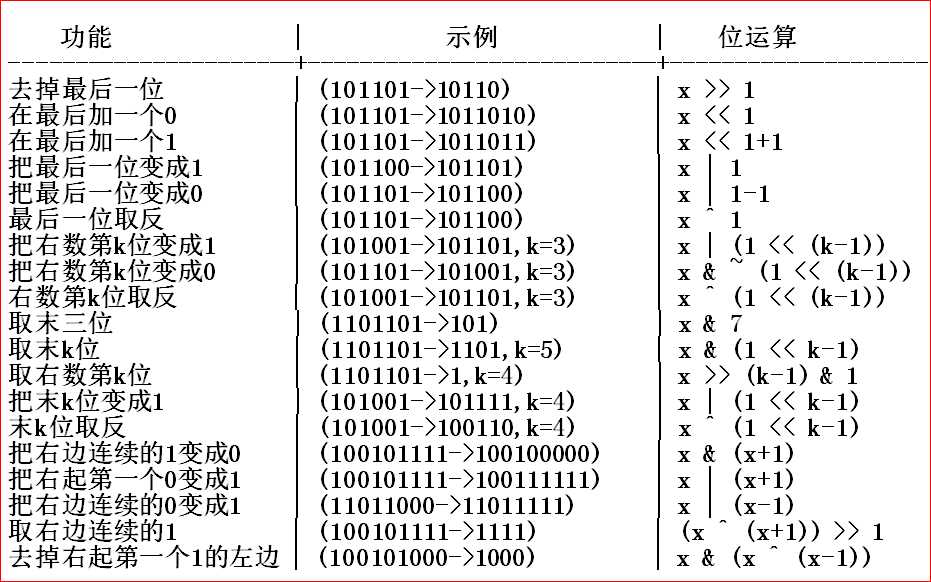
二：位運算

&：與運算，相同為1不同為0

| ：或運算，全0位0，否則為1

^：異或運算，不同為1，相同為0（也叫半加與運算）

<<：左移操作，x<<j，x在二進制下向左移j位,（也就是原來的數乘j即：x*=j）右邊用0填充，反碼不同，要用1填充（負數）

>>：右移操作，x>>j相當於x=/j，左邊反碼，補碼補1（負數）

例：

1.判斷一個數字x在二進制下的第i位是不是為1if(((i<<(i-1))&x)>0)

將1左移i-1位，相當於制造了一個只有第i位為1其他位都是0的二進制數，然後用該數與x做與運算

2.把一個數字x在二進制下的第x為更改為1

x|=(1<<(i-1))

eg：

有一個n*m的棋盤（1<=n<=5,1<=m<=1000）現有1*2和2*1的小木塊無數

要想蓋滿整個棋盤有多少種方法，答案大於1000000007，mod1000000007。

#include <cstdio>
#include <cstring>
#include <algorithm>     
#include <iostream>   
using namespace
 
 std;
int N, M;    //n,m分別代表棋盤的長寬
long long dp[1005][34];    //dp[i][j]表示對於前i-1行，第i行采用第j（一個十進制的數）種狀態時，得到的方案可行的總數　　
void dfs(int i,int j,int state,int nex)    //這裏i代表列數，j代表當前位數(也可以說是行數-1，初始時為0)，state代表狀態數，nex代表下一列出現的狀態
{
    if (j==N)    //用if判斷每種情況都嘗試去做，而不用if...else判斷
    {
        dp[i+1][nex]+=dp[i][state];
        
 
return;
    }
    if (((1<<j)&state)>0)    
        dfs(i,j+1,state,nex);    //如果這個位置已經被上一列所占用,直接跳過
    if (((1<<j)&state)==0)
        dfs(i,j+1,state,nex|(1<<j));       //如果這個位置是空的，嘗試放一個左右覆蓋1*2的木板
    if (j+1<N && ((1<<j)&state)==0 && ((1<<(j+1))&state)==0)
        dfs(i,j+2,state,nex);     //如果這個位置以及下一個位置都是空的，嘗試放一個上下覆蓋2*1的木板，而此時要跳過下一個木塊
    return;
}
int main()
{
    while (cin>>N>>M)
    {
        memset(dp,0,sizeof(dp));    
        dp[1][0]=1;    //初始化第一列狀態為0的方法數等於1
        for (int i=1;i<=M;i++)    //外層for循環遍歷每一列
        {
            for (int j=0;j<(1<<N);j++)    //內層for遍歷每一個列的所有狀態
                if (dp[i][j])    //只要dp[i][j]方法數不為空，就執行dfs方法
                {
                    dfs(i,0,j,0);
                }
        }
        cout<<dp[M+1][0]<<endl;    //最後dp[m+1][0]就是結果
    }
}

https://blog.csdn.net/harrypoirot/article/details/23163485

一個大佬講的狀壓dp

二：狀壓dp