• 前言

  本文只是用比較通俗的例子讓大家了解一下什麽是莫比烏斯反演，其中說明
  （明明都是瞎猜）可能有紕漏。本人也是個蒟蒻，未能給出珂學證明，還望多多指教。

• 理論基礎

1. “|”符號表示整除，
   a|b 表示b被a整除，也就是b有a這個因數，b=ka (k∈N)。
2. “∑ ”求和符號

• 是什麽

請先看這個例子：

假設有兩個函數F(n),f(d)，且d∈{x| x|n(即n被d整除)}
並有以下關系：F(n)等於所有f(d)之和。

比如：6能被1,2,3,6整除，所以F(6)=f(1)+f(2)+f(3)+f(6)
用一個公示表示就是：

由此可得到：

F(1)=f(1)

F(2)=f(1)+f(2)

F(3)=f(1)+ f(3)

F(4)=f(1)+f(2)+f(4)

F(5)=f(1)+f(5)

F(6)=f(1)+f(2)+f(3)+f(6)

F(7)=f(1)+f(7)

稍微變形得到：

f(1)=F(1)

f(2)=F(2)-f(1)=F(2)-F(1)

f(3)=F(3)-F(1)

f(4)=F(4)-f(2)-f(1)=F(4)-F(2)

f(5)=F(5)-F(1)

f(6)=F(6)-F(3)-F(2)+F(1)

f(7)=F(7)-F(1)

f(8)=F(8)-F(4)

emmmmm這樣如果我們知道各個F(n)的值我們肯定能算出各個f(d)的值，只要打表推就可以了，但仔細觀察一下，有沒有什麽規律呢？

好像每一個f(n)都由它所有的因子d∈{x| x|n(即n被d整除)}的F(d)乘上一個0或1或-1的系數再相加得到，我們就把這個系數也看成是d的一個函數μ(d)，稱作莫比烏斯函數。

那莫比烏斯函數的值我們怎麽知道呢？有沒有一個通項公式？

我們就從最特殊的f(6)著手：
f(6)=F(6)-F(3)-F(2)+F(1)
我們不妨這樣看：

f(6)=1×F(6/1)+(-1)×F(6/2)+(-1)×F(6/3)+1×F(6/6)

此時好像有點端倪了，我們可以將F()中每個分母看作d,且把1看做特殊情況：μ(1)=1,易看出μ(2)=-1,μ(3)=-1,μ(6)=1.

這時相信不少大佬已看出μ(d)的值與d本身互異質因子

假設一正整數d的互異質因子個數為k，則μ(d)=(-1)^k。
特殊的μ(1)=1.

那有些μ(d)卻等於0怎麽解釋呢？？？
比如：f(8)= F(8)-F(4),

根據上文的推測，我們知道,f(8)=μ(1)×F(8/1)+μ(2)×F(8/2)+μ(4)×F(8/4)+μ(8)×F(8/8)

再看看上文我們已有的結論，正整數d的互異質因子個數這就要求d必須能為k個互異且互質的數的乘積。但是4=2×2不滿足互異，8=2×4不滿足互質。

所以我們就猜想除1外不能由幾個互質且互異的正整數相乘得到的數d的莫比烏斯函數值為0,例：μ(4)=0,μ(8)=0。

下面總結一下：

- μ(d)函數是莫比烏斯函數，如果d=1，μ(d)=1

- 如果d為互異質數p1,p2…pk的乘積(若d本身是個質數就看是它本身一個的乘積)，則μ(d)=(?1)^k

- 否則，μ(d)=0 


然而，我們現在只是會求莫比烏斯函數值，什麽是莫比烏斯反演呢？

其實就是下面兩個定理：

 - 式1（約數關系）：若
 

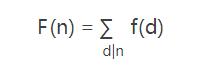
 則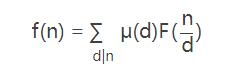

 - 式二（倍數關系）：若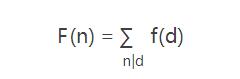

 則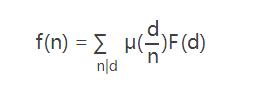

式1在開頭已經說過，式2也類似，還請大家拿出草稿紙多演算一下，才能領悟。

• 相關（不會證的）性質

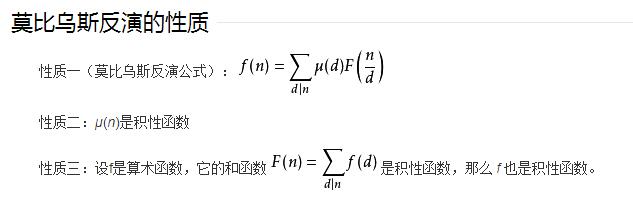
好吧我是從百科上截來的，不過我還找到了其他幾個（全都不會證）

• 對於大於1的正整數n

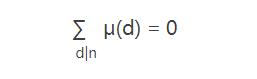
• 對於任意正整數n

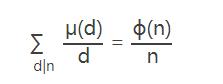
φ()就是歐拉函數，若不清楚的可以看我的這篇博客：
我又打廣告了

• 應用

線性方法求莫比烏斯函數值表

和歐式篩法很像，建議先了解歐式篩法原理，其他詳見代碼註釋

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn=19260817;
int n;
int prime[maxn];//記錄素數 
int mob[maxn];//記錄莫比烏斯函數值 
bool vis[maxn];
int cnt=0;//記錄素數個數 
void make_mob(int m)
{
    memset(vis,0,sizeof(vis));
    mob[1]=1;//特殊 
    for(int i=2;i<=m;i++)
    {
        if(!vis[i]){
            prime[++cnt]=i;
            mob[i]=-1;//素數的μ()為-1，
            //只有其本身一個互異互質因子 
        }
        for(int j=1;j<=cnt&&i*prime[j]<=m;j++)
        {
            vis[i*prime[j]]=1;//篩素數，不必多講
            if(i%prime[j]==0){
                mob[i*prime[j]]=0;break; 
            //設x=i*prime[j]很明顯它的兩個因子i與prime[j]不互質 
            //break;大家可以先去看看歐式篩素數原理理解這句話 
            }
            mob[i*prime[j]]=-mob[i];
        //不難理解，i*prime[j]比i多了一個因子 
        }
    }
}
int main()
{
    cin>>n;
    make_mob(n);
    for(register int i=1;i<=n;i++)
    {
        cout<<mob[i]<<‘ ‘;
        if(i%10==0)putchar(‘\n‘);
    }
    return 0;
} 

學習筆記--數論--莫比烏斯反演初認識