基於ANN的6種調制信號自動調制識別（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）
目的： 實現6種（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）調制信號自動調制識別。
條件：windows 10，MATLAB 2014a
內容： 本實驗設計了一個分層結構的MLP神經網絡分類器。該分類器使用BP算法，自適應改變判決門限，6種調制信號的整體平均識別率為96.94。
更多內容查看：word版（內附完整源代碼）下載地址：http://download.csdn.net/download/lanluyug/9923631
一、數字通信調制信號matlab實現原理
1.1二進制振幅鍵控（2ASK）
振幅鍵控，就是根據基帶信號改變載波的幅度。最簡單的實現方式是載波的頻率不變，使用二進制信號“0”和“1”控制。2ASK信號可以表示成一個單極性矩形脈沖序列與一個正弦波相乘，其時域表達式為:
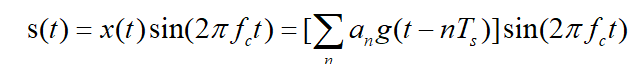
其中matlab代碼實現2ASK為：
% 2ASK signal
x=randint(1,M); %M為64，x為隨機生成的1*64的隨機矩陣（矩陣元素由0和1組成）
m=sin(2*pi*fc*t); %載波信號
y=ones(1,M*N); %M=64,N=200,y為1*12800的全1矩陣
for i=1:M
for j=1:N
y((i-1)*N+j)=x(i)*m(j); %隨機生成的2ASK信號
end
end
原理：使用randint()函數生成1*M的隨機矩陣（此矩陣由0和1兩種元素組成）；此時矩陣x=randint()可充當單極性矩形脈沖序列，最後兩層嵌套循環生成2ASK信號：y((i-1)*N+j)=x(i)*m(j);
1.2二進制頻移鍵控（2FSK）
頻移鍵控，就是根據基帶信號改變載波的頻率。二進制頻移鍵控，是指調制信號“0”和“1”分別對應載波的兩個頻率f1和f2。此時2FSK信號可以看成調整幅度為0和1的兩個2ASK信號的疊加，其時域表達式為：
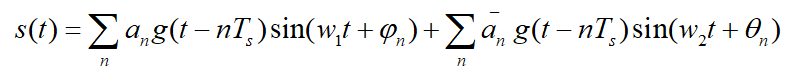
式子中g(t)為單個矩陣脈沖，脈寬為Ts
其中an取值如下：
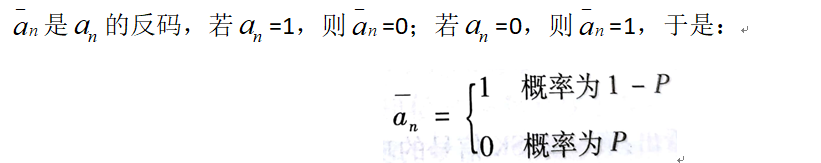
其中matlab代碼實現2FSK為：
%2FSK signal
x=randint(1,M);
m1=sin(2*pi*fc*t); %載頻信號1
m2=sin(2*pi*2*fc*t); %載頻信號2
y=zeros(1,M*N);
for i=1:M
if x(i)==1;
for j=1:N;
y((i-1)*N+j)=x(i)*m1(j); %碼元信息為1時，為m1頻率波形
end
elseif x(i)==0;
for j=1:N;
y((i-1)*N+j)=(1-x(i))*m2(j); %碼元信息為0時，為m2頻率波形
end
end
end
原理：使用randint()函數生成1*M的隨機矩陣（此矩陣由0和1兩種元素組成）；此時矩陣x=randint()可充當單極性矩形脈沖序列，然後兩層嵌套for循環加if判斷x[i]生成兩類2ASK信號，最後疊加成2FSK信號：x[i]=1時，y((i-1)*N+j)=x(i)*m1(j); x[i]=0時，y((i-1)*N+j)=(1-x(i))*m2(j)。
1.3二進制相移鍵控（2PSK）
二進制相移鍵控（2PSK）是載波的相位隨著二進制數字基帶信號而變化，而振幅和頻率保持不變。2PSK信號的時域表達式為：
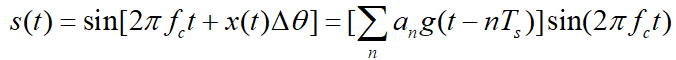
式子中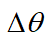
是相移常數，式子中是基帶序列為“0”和“1”控制。
%2PSK signal,
x=randint(1,M);
m1=sin(2*pi*fc*t);
m2=sin(2*pi*fc*t+pi);
y=zeros(1,M*N);
for i=1:M
if x(i)==1;
for j=1:N;
y((i-1)*N+j)=x(i)*m1(j);
end
elseif x(i)==0;
for j=1:N;
y((i-1)*N+j)=(1-x(i))*m2(j);
end
end
end
原理：使用randint()函數生成1*M的隨機矩陣（此矩陣由0和1兩種元素組成）；此時矩陣x=randint()可充當單極性矩形脈沖序列，然後兩層嵌套for循環加if判斷x[i]生成兩類相位相差π的2ASK信號，最後疊加成2PSK信號：當x[i]=1時，m1=sin(2*pi*fc*t); y((i-1)*N+j)=x(i)*m1(j); 當x[i]=0時，m2=sin(2*pi*fc*t+pi);
y((i-1)*N+j)=(1-x(i))*m2(j)。
1.4總結
4ASK,4FSK,4PSK調制信號matlab代碼采用類似手段構成，在此不作介紹，詳細信息可以參考最後附錄的源代碼。再者，本次實驗設置參數如下：載波頻率fc=20000；采樣頻率fs=40000；信息碼元長度=15*round(k*fs/fc); 信號長度t0=5.5; 采樣點個數Ns=256; 符號速率fd=200; 碼元個數M=64，信噪比SNR=5dB;更多細節可參考附錄源代碼，本人在多數代碼後面都寫有註釋。
二、自動調制識別設計與仿真
目前，自動調制識別方法可以分為兩大類：統計判決理論方法和統計模式識別方法。本次報告詞用後者。
一個通用的模式識別系統由信號預處理、特征提取和分類識別三部分組成。根據識別部分采用不同又可以分為基於決策理論的信號調制識別、基於人工神經網絡的信號調制識別和基於支持向量機的信號調制識別。下圖為自動調制識別一般流程：
2.1 調制信號特征參數選取
E.E.Azzouz和A.K.Nandi發表多篇調制信號識別的類似文章，利用他們提出的五個參數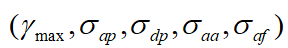
，采用判決數的方法對數字信號集（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）進行識別分類，在信噪比10dB時，識別率高於90%，在信噪比為20dB時，識別率高於96%。
2.2 神經網絡分類器概述
人工神經網絡（ANN）是仿生物神經網絡的結構提出的，他是由大量簡單的計算單元（節點）相互連接而構成的一種並行分布式處理網絡。神經網絡的分布處理以及它所特有的高度容錯性、自組織和自學習能力使它在自動調制識別領域具有很強的應用能力。
神經網絡分類器一般由許多個計算節點組成，每個節點只有一個輸出，而這個輸出可以連接很多其他的計算節點，每個節點的輸入有很多個連接通路，每個連接通路對應於一個連接權系數。
（1） 每個節點具有一個狀態變量；
（2） 節點i到節點j有一個權系數；
（3） 每個節點有一個閾值；
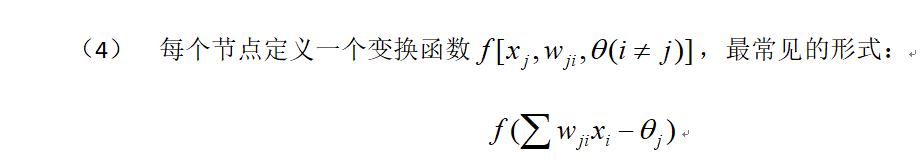
在通信信號自動調制識別應用中，一般選用基於有監督訓練的神經網絡模型作為分類器，特別是各種有監督訓練的前饋神經網絡，其中的MLP（多層感知器）和RBF（徑向基函數神經網絡）是最常用的兩種模型。
2.3分類器設計
（1）隱含層數的選擇
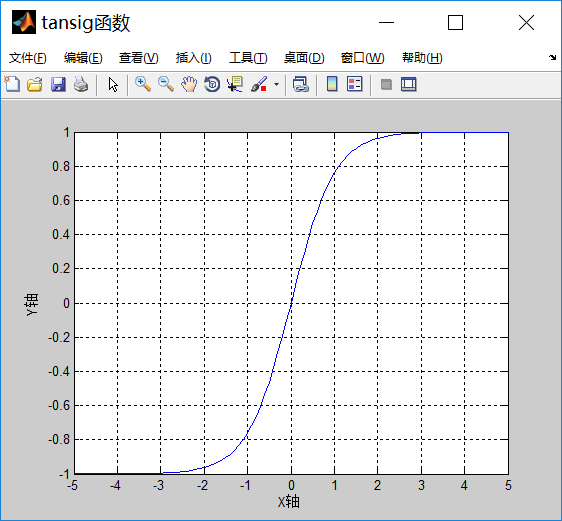
本文設計的神經網絡分類器是一個具有三層網絡結構的神經網絡分類器：輸入層、一個隱藏層和輸出層。輸入層到隱含層采用的傳遞函數（激活函數）是S型對數函數logsig，隱含層到輸出層采用的傳遞函數是S型正切函數tansig。
兩個函數的笛卡爾坐標圖分別為：
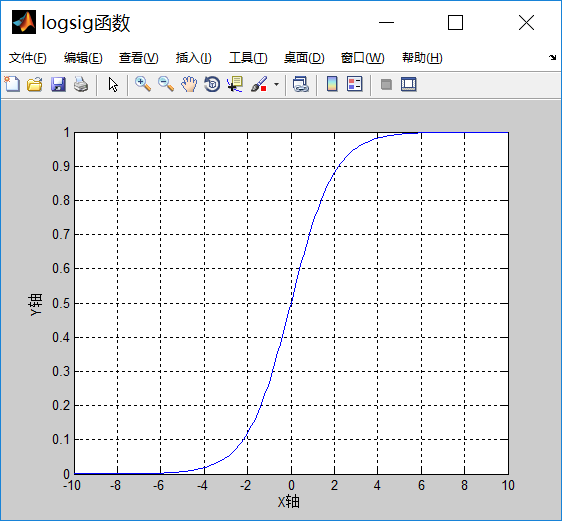
（2）隱含層節點數的確定
由於ANN是一個極為復雜的非線性動態系統，因此很難找到有關其特征、容量一類的簡潔解析表達式，常用的一個確定隱含層節點的方法為試湊法：先設置較少的隱含節點訓練網絡，然後逐漸增加隱含點，用同一樣本集進行訓練，從中確定網絡誤差最小時對應的隱節點數。在用試湊法時，可以用一些確定的隱節點數的經驗公式。
ANN最常見的試湊法的經驗公式如下：
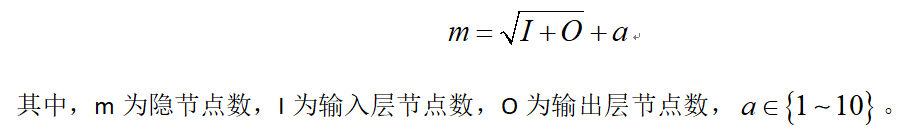
（3）訓練樣本集與測試樣本集
6種（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）調制信號的目標結果以1，2，3，4，5，6來表示。本文選取的訓練樣本集包含了這六種調制信號的特征參數向量各200組，測試樣本集為包含了這6種調制信號特征參數向量各60組。
% 6種（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）調制信號的自動調制識別matlab2014a
clear all;
close all;
echo off; %神經網絡訓練時不顯示每一步的梯度和誤差性能
fc=20000; %載波頻率
fs=40000; %采樣速率
k=2; %常用系數k為2
code_size=15*round(k*fs/fc); %信息碼元長度
t0=5.5; %信號長度
Ns=256; %采樣點個數
fd=200; %符號速率
ts=1/fs; %采樣周期
M=64 %碼元個數
ti=1/fd; %碼元間隔 N=200
N=ti/ts
t=[0:ts:t0];
select=menu(‘調制方式‘,‘2ASK‘,‘2FSK‘,‘2PSK‘,‘4ASK‘,‘4FSK‘,‘4PSK‘);
switch select
case 1, % 2ASK signal
x=randint(1,M); %M為64，x為隨機生成的1*64的隨機矩陣（矩陣元素由0和1組成）
m=sin(2*pi*fc*t); %載波信號
y=ones(1,M*N); %M=64,N=200,y為1*12800的全1矩陣
for i=1:M
for j=1:N
y((i-1)*N+j)=x(i)*m(j); %隨機生成的2ASK信號
end
end
T=zeros(6,50); %T為6*50的全0矩陣
T(1,1:50)=1; %將矩陣T第一行全部置1
case 2, %2FSK signal
x=randint(1,M);
m1=sin(2*pi*fc*t); %載頻信號1
m2=sin(2*pi*2*fc*t); %載頻信號2
y=zeros(1,M*N);
for i=1:M
if x(i)==1;
for j=1:N;
y((i-1)*N+j)=x(i)*m1(j); %碼元信息為1時，為m1頻率波形
end
elseif x(i)==0;
for j=1:N;
y((i-1)*N+j)=(1-x(i))*m2(j); %碼元信息為0時，為m2頻率波形
end
end
end
T=zeros(6,50);
T(2,1:50)=1;
case 3, %2PSK signal,
x=randint(1,M);
m1=sin(2*pi*fc*t);
m2=sin(2*pi*fc*t+pi);
y=zeros(1,M*N);
for i=1:M
if x(i)==1;
for j=1:N;
y((i-1)*N+j)=x(i)*m1(j);
end
elseif x(i)==0;
for j=1:N;
y((i-1)*N+j)=(1-x(i))*m2(j);
end
end
end
T=zeros(6,50);
T(3,1:50)=1;
case 4, % 4ASK signal
x=randint(1,M,4);
m=sin(2*pi*fc*t);
y=ones(1,M*N);
for i=1:M
if x(i)==0;
for j=1:N
y((i-1)*N+j)=x(i)*m(j);
end
elseif x(i)==1;
for j=1:N
y((i-1)*N+j)=x(i)*m(j);
end
elseif x(i)==2;
for j=1:N
y((i-1)*N+j)=x(i)*m(j);
end
elseif x(i)==3;
for j=1:N
y((i-1)*N+j)=x(i)*m(j);
end
end
end
T=zeros(6,50);
T(4,1:50)=1;
case 5, % 4FSK signal
x=randint(1,M,4);
m1=sin(2*pi*fc*t);
m2=sin(2*pi*2*fc*t);
m3=sin(2*pi*3*fc*t);
m4=sin(2*pi*4*fc*t);
y=zeros(1,M*N);
for i=1:M
if x(i)==0;
for j=1:N
y((i-1)*N+j)=(1-x(i))*m1(j);
end
elseif x(i)==1;
for j=1:N
y((i-1)*N+j)=x(i)*m2(j);
end
elseif x(i)==2;
for j=1:N
y((i-1)*N+j)=(x(i)-1)*m3(j);
end
elseif x(i)==3;
for j=1:N
y((i-1)*N+j)=(x(i)-2)*m4(j);
end
end
end
plot(y)
T=zeros(6,50);
T(5,1:50)=1;
case 6, %4PSK signal
x=randint(1,M,4);
m1=sin(2*pi*fc*t);
m2=sin(2*pi*fc*t+pi/2);
m3=sin(2*pi*fc*t+pi);
m4=sin(2*pi*fc*t+3*pi/2);
y=zeros(1,M*N);
for i=1:M
if x(i)==0;
for j=1:N
y((i-1)*N+j)=(1-x(i))*m1(j);
end
elseif x(i)==1;
for j=1:N
y((i-1)*N+j)=x(i)*m2(j);
end
elseif x(i)==2;
for j=1:N
y((i-1)*N+j)=(x(i)-1)*m3(j);
end
elseif x(i)==3;
for j=1:N
y((i-1)*N+j)=(x(i)-2)*m4(j);
end
end
end
T=zeros(6,50);
T(6,1:50)=1;
end
SNR=5; %定義信噪比，單位dB
sigpow=mean(abs(y).^2); %power of input signal
noisefac=10^(-SNR/10);
noise=randn(1,size(y,2));
noise=noise*(sqrt(sigpow*noisefac)/sqrt(mean(noise.^2))); %產生所需的高斯噪聲
ynoise=noise+y; %加噪後的信號
for n=1:1:50
m=n*Ns;
x=(n-1)*Ns;
for i=x+1:m; %提取信號段
y0(i)=ynoise(i);
end
Y=fft(y0); %調制信號的傅立葉變換
y1=hilbert(y0); %實信號的解析式
z=abs(y0); %實信號的瞬時幅度
phase=angle(y1); %實信號的瞬時相位
add=0; %求Rmax
for i=x+1:m;
add=add+z(i);
end
ma=add/Ns; %瞬時幅度的平均值
y2=z./ma ; %幅度比,即為文獻中的an(i)
y2n=y2-1; %歸一化瞬時幅度
Rmax=max(abs(fft(y2n.^2)/Ns));%零中心歸一化瞬時幅度的譜密度的最大值
Xcn=0;
Ycn=0;
for i=x+1:m;
Xcn=Xcn+y2n(i).*y2n(i);
Ycn=Ycn+abs(y2n(i));
end
Xcnav=Xcn/Ns;
Ycnav=(Ycn/Ns).*(Ycn/Ns);
deltaaa=sqrt(Xcnav-Ycnav); %零中心歸一化瞬時幅度絕對值得標準偏差
if phase(2+x)-phase(1+x)>pi; %修正相位序列
Ck(1+x)=-2*pi;
elseif phase(1+x)-phase(2+x)>pi;
Ck(1+x)=2*pi;
else Ck(1+x)=0;
end
for i=x+2:m-1;
if phase(i+1)-phase(i)>pi;
Ck(i)=Ck(i-1)-2*pi;
elseif phase(i)-phase(i+1)>pi
Ck(i)=Ck(i-1)+2*pi;
else
Ck(i)=Ck(i-1);
end
end
if -phase(m)>pi;
Ck(m)=Ck(m-1)-2*pi;
elseif phase(m)>pi;
Ck(m)=Ck(m-1)+2*pi;
else Ck(m)=Ck(m-1);
end
phase1=phase+Ck %去相位卷疊後的相位序列
phasenl=phase1-2*pi*fc*i/fs; %非線性相位
at=1; %判決門限電平
a=0; %求取零中心非弱信號段瞬時相位非線性分量絕對值的標準偏差和零中心非弱信號段瞬時相位非線性分量的標準偏差
b=0;
d=0;
c=0;
for i=x+1:m;
if y2(i)>at
c=c+1;
phasesquare(i)=phasenl(i).*phasenl(i);
a=a+phasesquare(i);
phaseabs(i)=abs(phasenl(i));
b=b+phaseabs(i);
d=d+phasenl(i)
end
end
a1=a/c;
b1=(b/c).*(b/c);
d1=(d/c).*(d/c);
deltaap=sqrt(a1-b1); %零中心非弱信號段瞬時相位非線性分量絕對值的標準偏差
deltadp=sqrt(a1-d1); %零中心非弱信號段瞬時相位非線性分量的標準偏差
freqN(i)=phase1(i)-phase1(i-1);
for i=x+1:m;
if i>at;
c=c+1;
freqNsquare(i)=freqN(i).*freqN(i);
a=a+freqNsquare(i);
b=b+freqN(i);
end
end
a1=a/c;
b1=(b/c)^2;
deltaaf=sqrt(a1-b1); %零中心歸一化非弱信號段瞬時頻率絕對值得標準偏差
Pi=rand(5,50);
P0=rand(5,50);
Pi(5*n-4)=Rmax;
Pi(5*n-3)=deltaap;
Pi(5*n-2)=deltadp;
Pi(5*n-1)=deltaaa;
Pi(5*n)=deltaaf;
end
%采用BP網絡
%NEWCF--生成一個新的前向神經網絡
%TRAIN--對網絡進行訓練
% 定義訓練樣本
%Pi為輸入矢量
%T為目標矢量
%創建一個新的前向神經網絡
net=newff(minmax(Pi),[5,15,6],{‘tansig‘,‘purelin‘,‘logsig‘},‘traingda‘);
%設置訓練參數
net.trainParam.show=50; %兩次顯示之間的訓練步數
net.trainParam.lr=1; %
net.trainParam.mc=0.5;
net.trainParam.epochs=2000; %訓練次數
net.trainParam.goal=1e-3; %訓練目標
%調用TRAINGDM算法訓練網絡
[net,tr]=train(net,Pi,T);
%對網絡進行仿真
A=sim(net,Pi);
E=T-A;
T1=zeros(6,50);
T1(1,1:50)=1;
E1=0;
for c=1:1:300
Eout=(T1(c)-A(c))^2;
E1=Eout+E1 ;
end
T2=zeros(6,50);
T2(2,1:50)=1;
E2=0;
for c=1:1:300
Eout=(T2(c)-A(c))^2;
E2=Eout+E2;
end
T3=zeros(6,50);
T3(3,1:50)=1;
E3=0;
for c=1:1:300
Eout=(T3(c)-A(c))^2;
E3=Eout+E3;
end
T4=zeros(6,50);
T4(4,1:50)=1;
E4=0;
for c=1:1:300
Eout=(T4(c)-A(c))^2;
E4=Eout+E4;
end
T5=zeros(6,50);
T5(5,1:50)=1;
E5=0;
for c=1:1:300
Eout=(T5(c)-A(c))^2;
E5=Eout+E5;
end
T6=zeros(6,50);
T6(6,1:50)=1;
E6=0;
for c=1:1:300
Eout=(T6(c)-A(c))^2;
E6=Eout+E6;
end
E0=0;
if (E1>E2)
E0=E2;
else E0=E1;
end
if (E3<E0)
E0=E3;
end
if (E4<E0)
E0=E4;
end
if (E5<E0)
E0=E5;
end
if (E6<E0)
E0=E6;
end
E0;
if (E0==E1)
type=menu(‘輸入信號是‘,‘2ASK信號‘);
end
if (E0==E2)
type=menu(‘輸入信號是‘,‘2FSK信號‘);
end
if(E0==E3)
type=menu(‘輸入信號是‘,‘2PSK信號‘);
end
if(E0==E4)
type=menu(‘輸入信號是‘,‘4ASK信號‘);
end
if(E0==E5)
type=menu(‘輸入信號是‘,‘4FSK信號‘);
end
if(E0==E6)
type=menu(‘輸入信號是‘,‘4PSK信號‘);
end
%計算正確識別率sita
sita=0;
j=0;
for nn=1:1:50
Ee=(E(6*nn-5)^2)+(E(6*nn-4)^2)+(E(6*nn-3)^2)+(E(6*nn-2)^2)+(E(6*nn-1)^2)+(E(6*nn)^2);
if Ee<0.01
j=j+1
end
end
sita=j/50;
type=menu(‘正確識別率為:‘,sita*100,‘％‘)
基於ANN的6種調制信號自動調制識別（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）